ग्राफ़ीय विधि से निम्न रैखिक प्रोग्रामन समस्या को हल कीजिए:
निम्न अवरोधों के अंतर्गत Z = -3x + 4y का न्यूनतमीकरण कीजिए:
x + 2y $\leq$ 8, 3x + 2y $\leq$ 12, x $\geq$ 0, y $\geq$ 0
निम्न अवरोधों के अंतर्गत Z = -3x + 4y का न्यूनतमीकरण कीजिए:
x + 2y $\leq$ 8, 3x + 2y $\leq$ 12, x $\geq$ 0, y $\geq$ 0
Exercise-12.1-2
Download our app for free and get started
हमको उद्देश्य फलन
Z = -3x + 4y ...(i)
का निम्न व्यतरोधों के अंतर्गत अधिकतम मान ज्ञात करना है।
x + 2y $\leq$ 8 ...(ii)
3x + 2y $\leq$ 12 ...(iii)
x $\geq$ 0, y $\geq$ 0 ...(iv)
सर्वप्रथम रेखा x + 2y = 8 का ग्राफ खींचते हैं।
Z = -3x + 4y ...(i)
का निम्न व्यतरोधों के अंतर्गत अधिकतम मान ज्ञात करना है।
x + 2y $\leq$ 8 ...(ii)
3x + 2y $\leq$ 12 ...(iii)
x $\geq$ 0, y $\geq$ 0 ...(iv)
सर्वप्रथम रेखा x + 2y = 8 का ग्राफ खींचते हैं।
| x | 0 | 8 |
| y | 4 | 0 |
(0, 0) असमिका x + 2y $\leq$ 8 में रखने पर,
0 + 0 $\leq$ 8 $\Rightarrow $ 0 $\leq$ 8 (जोकि सत्य है)
अतः अर्द्धतल मूलबिंदु की ओर स्थित है।
चूँकि, x, y $\geq$ 0
अतः सुसंगत क्षेत्र प्रथम चतुर्थांश में है।
अब, रेखा 3x + 2y = 12 का ग्राफ खींचते हैं।
| x | 0 | 8 |
| y | 6 | 0 |
(0, 0) असमिका 3x + 2y $\leq$ 12 में रखने पर,
3 $\times$ 0 $\leq$ 12 $\Rightarrow$ 0 $\leq$ 12 (जोकि सत्य है)
अतः अर्द्धतल मूलबिंदु की ओर है।
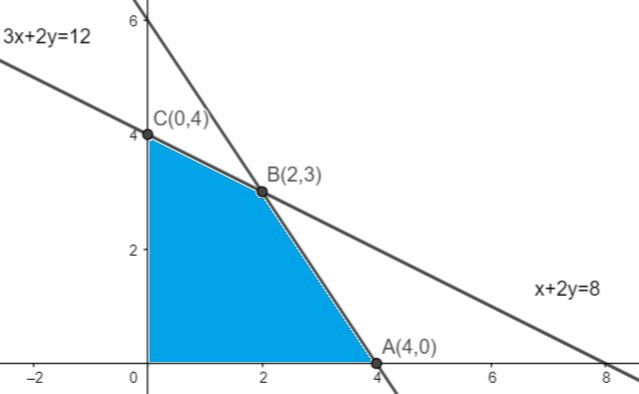
अतः सुसंगत क्षेत्र OABCO है।
समीकरण x + 2y = 8 तथा 3x + 2y = 12 को हल करने पर, x = 2 तथा y = 3 प्राप्त होता है।
$\therefore$ प्रतिच्छेद बिंदु B(2, 3) है।
इस प्रकार, सुसंगत क्षेत्र के शीर्ष बिंदु O(0, 0), A(4, 0), B(2, 3) तथा (0, 4) है। इन शीर्ष बिंदुओं पर Z का मान निम्न है।
| शीर्ष बिंदु | Z = -3x + 4y |
| O(0, 0) | 0 |
| A(4, 0) | -12 $\rightarrow$ अधिकतम |
| B(2, 3) | 6 |
| C(0, 4) | 16 |
अतः Z का निम्नतम मान -12 है जोकि बिंदु A(4, 0) पर प्राप्त होता है।
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1आलेख द्वारा निम्न रैखिक प्रोग्रामन समस्या को हल कीजिए:View Solution
निम्न व्यवरोधों के अंतर्गत
x + y $\leq$ 50 ...(i)
3x + y $\leq$ 90 ...(ii)
x $\geq$ 0, y $\geq$ 0 ...(iii)
Z = 4x + y का अधिकतम मान ज्ञात कीजिए। - 2आलेखीय विधि से निम्न समस्या को हल कीजिए:View Solution
निम्न व्यवरोधों के अंतर्गत
x + 3y $\leq$ 60 ...(i)
x + y $\geq$ 10 ...(ii)
x $\leq$ y ...(iii)
x $\geq$ 0, y $\geq$ 0 ...(iv)
Z = 3x + 9y का न्यूनतम और अधिकतम मान ज्ञात कीजिए। - 3View Solutionएक कुटीर उद्योग निर्माता पैडेस्टल लैंप और लकड़ी के शेड बनाता है। प्रत्येक के निर्माण में एक रगड़ने/काटने और एक स्प्रेयर की आवश्यकता पड़ती है। एक लैंप के निर्माण में 2 घंटे रगड़ने/काटने और 3 घंटे स्प्रेयर की आवश्यकता होती है, जबकि एक शेड के निर्माण में 1 घंटा रगडने/काटने और 2 घंटे स्प्रेयर की आवश्यकता होती है। स्प्रेयर की मशीन प्रतिदिन अधिकतम 20 घंटे और रगड़ने/काटने की मशीन प्रतिदिन अधिकतम 12 घंटे के लिए उपलब्ध है। एक लैंप की बिक्री पर ₹5 और एक शेड की बिक्री पर ₹3 का लाभ होता है। यह मानते हुए कि सभी निर्मित लैंप और शेड बिक जाते है, तो बताइए वह निर्माण की प्रतिदिन कैसी योजना बनाए कि लाभ अधिकतम हो?
- 4View Solutionएक कंपनी प्लाईवुड के अनूठे स्मृति चिह्न का निर्माण करती है। A प्रकार के प्रति स्मृति चिह्न के निर्माण में 5 मिनट काटने और 10 मिनट जोड़ने में लगते हैं। B प्रकार के प्रति स्मृति चिह्न के लिए 8 मिनट काटने और 8 मिनट जोड़ने में लगते हैं। दिया गया है कि काटने के लिए कुल समय 3 घंटे 20 मिनट तथा जोड़ने के लिए 4 घंटे उपलब्ध हैं। प्रत्येक A प्रकार के स्मृति चिन्न पर ₹5 और प्रत्येक B प्रकार के स्मृति चिन्न पर ₹6 का लाभ होना है। ज्ञात कीजिए कि लाभ के अधिकतमीकरण के लिए प्रत्येक प्रकार के कितने-कितने स्मृति चिह्नों का कंपनी द्वारा निर्माण होना चाहिए?
- 5View Solutionएक निर्माणकर्ता नट और बोल्ट का निर्माण करता है। एक पैकेट नटों के निर्माण में मशीन A पर एक घंटा और मशीन B पर 3 घंटे काम करना पड़ता है, जबकि एक पैकेट बोल्ट के निर्माण में 3 घंटे मशीन A पर और 1 घंटा मशीन B पर काम करना पड़ता है। वह नटों से ₹17.50 प्रति पैकेट और बोल्टों पर ₹7.00 प्रति पैकेट लाभ कमाता है। यदि प्रतिदिन मशीनों का अधिकतम उपयोग 12 घंटे किया जाए तो प्रत्येक (नट और बोल्ट) के कितने पैकेट उत्पादित किए जाएँ ताकि अधिकतम लाभ कमाया जा सके।
- 6View Solutionएक किसान दो प्रकार के चारे P और Q को मिलाता (मिश्रण) है। P प्रकार के चारे, जिसका मूल्य ₹250 प्रति थैला जोकि पोषक तत्व A के 3 मात्रक, तत्व B के 2.5 मात्रक और तत्व C के 2 मात्रक रखता है जबकि Q प्रकार का चारा जिसका मूल्य ₹200 प्रति थैला है, पोषक तत्व A का 1.5 मात्रक, तत्व B का 11.25 मात्रक और तत्व C के तीन मात्रक रखता है। पोषक तत्वों A, B और C की न्यूनतम आवश्यकताएँ क्रमशः 18 मात्रक, 45 मात्रक और 24 मात्रक हैं। प्रत्येक प्रकार के थैलों की संख्या ज्ञात कीजिए ताकि मिश्रण के प्रत्येक थैले का मूल्य न्यूनतम हो? मिश्रण के प्रत्येक थैले का न्यूनतम मूल्य क्या है?
- 7View Solutionएक तेल कारखाने में दो डिपो A तथा B हैं, जिनकी क्षमताएँ क्रमशः 7000 लिटर और 4000 लिटर की हैं। कारखाने द्वारा तीन पेट्रोल पंपों D, E और F के लिए आपूर्ति करनी है, जिनकी आवश्यकताएँ क्रमशः 4500 लिटर, 3000 लिटर और 3500 लिटर की है। डिपो से पेट्रोल पंपों की दूरियाँ (km में) निम्नांकित सारणी के अनुसार है:
दूरियाँ (km में) को/से A B D 7 3 E 6 4 F 3 2 यह मानते हुए कि परिवहन व्यय प्रति 10 लिटर पर प्रति किलोमीटर 1 रुपया है, ज्ञात कीजिए कि कैसी आपूर्ति योजना अपनाई जाए, जिससे परिवहन व्यय का न्यूनतमीकरण हो जाए? न्यूनतम व्यय क्या है?
- 8दिखाइए कि Z का न्यूनतम मान दो बिंदुओं से अधिक बिंदुओं पर घटित होता है।View Solution
निम्न अवरोधों के अंतर्गत Z = x + y का अधिकतमीकरण कीजिए:
x - y $\leq$ -1, -x + y $\leq$ 0, x, y $\geq$ 0 - 9View Solutionएक आहारविद् दो प्रकार के भोज्यों X और Y को इस प्रकार मिलाना चाहता है कि मिश्रण में विटामिन A, की कम से कम 10 मात्रक, विटामिन B की कम से कम 12 मात्रक और विटामिन C की 8 मात्रक हों 1 kg भोज्यों में विटामिनों की मात्रा निम्नलिखित सारणी में दी गई है।
भोज्य विटामिन A विटामिन B विटामिन C X 1 2 3 Y 2 2 1 भोज्य X के 1 kg का मूल्य ₹16 और भोज्य y के 1 kg का मूल्य ₹20 है। वांछित आहार के लिए मिश्रण का न्यूनतम मूल्य ज्ञात कीजिए।
- 10ग्राफ़ीय विधि से निम्न रैखिक प्रोग्रामन समस्या को हल कीजिए:View Solution
निम्न अवरोधों के अंतर्गत Z = 3x + 4y का अधिकतमीकरण कीजिए:
x + y $\leq$ 4, x $\geq$ 0, y $\geq$ 0