एक $5 m$ लंबी सीढ़ी दीवार के सहारे झुकी है। सीढ़ी का नीचे का सिरा, जमीन के अनुदिश, दीवार से दूर $2 \ cm/ s$ की दर से खींचा जाता है। दीवार पर इसकी ऊँचाई किस दर से घट रही है जबकि सीढ़ी के नीचे का सिरा दीवार से $4 m$ दूर है?
Exercise-6.1-10
Download our app for free and get started
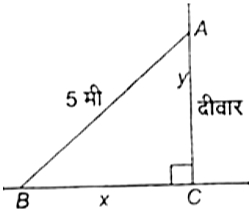
मान लीजिए $AB = 5$ मी सीढ़ी की लंबाई है और $y$ दीवार की ऊँचाई है जिस पर सीढ़ी झुकी है और सीढ़ी का पाद $B$ पर है, जहाँ से $C$ की दूरी $($दीवार से$) x$ है।
दिया गया है कि सीढ़ी का नीचे का सिरा जमीन के अनुदिश, दीवार से दूर $2$ सेमी/से की दर से खींचा जाता है।
$\therefore \frac{d x}{d t} = 2$ सेमी/से
जैसा कि हम जानते हैं कि $\triangle ABC$ समकोण त्रिभुज है, इसलिए पाइथागोरस प्रमेय द्वारा,
$x^2+ y^{2 }= 5^{2 ...}(i)$
जब $x = 4,$ तब $y^{2 }= 5^{2 }- 4^2$
$ \Rightarrow y = \sqrt{25-16}$
$ \Rightarrow y = 3$ मी
समी $(i)$ को समय $(t)$ के सापेक्ष दोनों ओर का अवकलन करने पर,
$2x \frac{d x}{d t} + 2y \frac{d y}{d t} = 0$
$\Rightarrow x \frac{d x}{d t} + y \frac{d y}{d t} = 0$
$\Rightarrow 4 \times 2 + 3 \times \frac{d y}{d t} = 0 (\therefore x = 4$ और $\frac{d x}{d t} = 2)$
$\Rightarrow \frac{d y}{d t} = \frac{-8}{3}$
$\Rightarrow$ दीवार पर सीढ़ी की ऊँचाई $\frac{d y}{d t} = \frac{-8}{3}$ सेमी/से की दर से घट रही है।
$($ऋणात्मक चिन्ह यह दर्शाता है कि दीवार पर सीढ़ी की ऊँचाई $\frac{8}{3}$ सेमी/से की दर से घट रही है$)$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$x = 2$ पर वक्र $y = x^{3 }- x$ की स्पर्श रेखा की प्रवणता ज्ञात कीजिए।View Solution
- 2बिंदु $(0, c)$ से परवलय $y = x^2$की न्यूनतम दूरी ज्ञात कीजिए जहाँ $\frac{1}{2} \leq c \leq 5$ है।View Solution
- 3किसी आयत की लंबायीं $x, 3 \ cm/min$ की दर से घट रही है और चौड़ाई $y, 2 \ cm/min$ की दर से बढ़ रही है। जब $x = 10 \ cm$ और $y = 6 \ cm$ है तब आयत केView Solution
- परिमाप और
- क्षेत्रफल में परिवर्तन की दर ज्ञात कीजिए।
- 4किसी वस्तु की $x$ इकाइयों के उत्पादन में कुल लागत $C(x)$ रुपये में $C(x) = 0.005 x^3 - 0.02 x^2+ 30x + 5000$ से प्रदत्त है। सीमांत लागत ज्ञात कीजिए जब $3$ इकाई उत्पादित की जाती है। जहाँ सीमांत लागत $($marginal cost या $MC)$ से हमारा अभिप्राय किसी स्तर पर उत्पादन के संपूर्ण लागत में तात्कालिक परिवर्तन की दर से है।View Solution
- 5सिद्ध कीजिए कि वक्र $x = y^2$ और $xy = k$ एक दूसरे को समकोण$*$ पर काटती है, यदि $8k^{2 }= 1$ है।View Solution
- 6उन अंतरालों को ज्ञात कीजिए जिनमें फलन f(x) = $ \frac{3}{10} x^{4}$ - $\frac{4}{5} x^{3}$ - $3 x^{2}$ + $\frac{36}{5} x$ + 11View Solution
- वर्धमान
- ह्यसमान है।
- 7वक्र $x^{2 }= 4y$ के किसी बिंदु पर अभिलंब का समीकरण ज्ञात कीजिए जो बिंदु $(1, 2)$ से होकर जाता है।View Solution
- 8सिद्ध कीजिए कि वक्र $y = 7x^3 + 11$ के उन बिंदुओं पर स्पर्श रेखाएँ समांतर है जहाँ $x = 2$ तथा $x = - 2$ है।View Solution
- 9वक्र $y = x^3 - 11x + 5$ पर उस बिंदु को ज्ञात कीजिए जिस पर स्पर्श रेखा $y = x - 11$ है।View Solution
- 10$f(x) = x^2, x \in R$ से प्रदत्त फलन $f$ के उच्चतम और निम्नतम मान, यदि कोई हों तो, ज्ञात कीजिए।View Solution