एक आलू दौड़ $($Potato race$)$ में, प्रारंभिक स्थान पर एक बाल्टी रखी हुई है, जो पहले आलू से $5 m$ की दूरी पर है, तथा अन्य आलुओं को एक सीधी रेखा में परस्पर $3 m$ की दूरियों पर रखा गया है। इस रेखा पर $10$ आलू रखे गए हैं $($देखिए संलग्न आकृति$)।$
प्रत्येक प्रतियोगी बाल्टी से चलना प्रारंभ करती है, निकटतम आलू को उठाती है, उसे लेकर वापस आकर दौड़ कर बाल्टी में डालती है, दूसरा आलू उठाने के लिए वापस दौड़ती है, उसे उठाकर वापस बाल्टी में डालती है और वह ऐसा तब तक करती रहती है जब तक सभी आलू बाल्टी में न आ जाएँ। इसमें प्रतियोगी को कुल कितनी दूरी दौड़नी पड़ेगी?

$[$संकेत: पहले और दूसरे आलुओं को उठाकर बाल्टी में डालने तक दौड़ी गई दूरी $= 2\times 5 + 2\times (5 + 3)$ है$।]$
प्रत्येक प्रतियोगी बाल्टी से चलना प्रारंभ करती है, निकटतम आलू को उठाती है, उसे लेकर वापस आकर दौड़ कर बाल्टी में डालती है, दूसरा आलू उठाने के लिए वापस दौड़ती है, उसे उठाकर वापस बाल्टी में डालती है और वह ऐसा तब तक करती रहती है जब तक सभी आलू बाल्टी में न आ जाएँ। इसमें प्रतियोगी को कुल कितनी दूरी दौड़नी पड़ेगी?

$[$संकेत: पहले और दूसरे आलुओं को उठाकर बाल्टी में डालने तक दौड़ी गई दूरी $= 2\times 5 + 2\times (5 + 3)$ है$।]$
Exercise-5.3-20
पहले आलू को उठाने और टोकरी में डालने में तय की गई दूरी $= 2\times 5 m$
दूसरे आलू को उठाने और टोकरी में डालने में तय की गई दूरी $= 2\times (5 + 3) m$
तीसरे आलू को उठाने और टोकरी में डालने में तय की गई दूरी $= 2\times (5 + 6) m$
प्रतियोगी द्वारा दौड़ कर तय की गई दूरी $= 2\times 5 + 2\times (5 + 3) + 2\times (5 + 6) + ... 10$ पदों तक
$= 10 + 16 + 22 + ....$ जो कि एक $A.P.$ है
यहाँ, $a = 10, d = 16 - 10 = 6, n = 10$
$\therefore S_{10} =\frac{10}{2}[2\times 10 + (10 - 1) 6]$
$[\because S_n =\frac{n}{2}[2a(n - 1)d]]$
$= 5\times [20 + 54] = 5\times 74 = 370$
अतः प्रतियोगी द्वारा दौड़ कर कुल तय की गई दूरी $= 370 m$
दूसरे आलू को उठाने और टोकरी में डालने में तय की गई दूरी $= 2\times (5 + 3) m$
तीसरे आलू को उठाने और टोकरी में डालने में तय की गई दूरी $= 2\times (5 + 6) m$
प्रतियोगी द्वारा दौड़ कर तय की गई दूरी $= 2\times 5 + 2\times (5 + 3) + 2\times (5 + 6) + ... 10$ पदों तक
$= 10 + 16 + 22 + ....$ जो कि एक $A.P.$ है
यहाँ, $a = 10, d = 16 - 10 = 6, n = 10$
$\therefore S_{10} =\frac{10}{2}[2\times 10 + (10 - 1) 6]$
$[\because S_n =\frac{n}{2}[2a(n - 1)d]]$
$= 5\times [20 + 54] = 5\times 74 = 370$
अतः प्रतियोगी द्वारा दौड़ कर कुल तय की गई दूरी $= 370 m$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1खाते में प्रत्येक वर्ष का मिश्रधन, जबकि $₹ 10000$ की राशि $8\%$ वार्षिक की दर से चक्रवृद्धि ब्याज पर जमा की जाती है। क्या यह स्थिति $A.P.$ है और क्यों?View Solution
- 2किसी $A.P.$ के तीसरे और सातवें पदों का योग $6$ है और उनका गुणनफल $8$ है। इस $A.P.$ के प्रथम $16$ पदों का योग ज्ञात कीजिए।View Solution
- 3केंद्र $A$ से आरम्भ करते हुए बारी$-$बारी से केंद्रों $A$ और $B$ को लेते हुए, त्रिज्याओं $0.5 \ cm, 1.0 \ cm, 1.5 \ cm, 2.0 \ cm, ...$ वाले उत्तरोत्तर अर्धवृत्तों को खींचकर एक सर्पिल $($Spiral$)$ बनाया गया है जैसा कि संलग्न आकृति में दर्शाया गया है। तेरह क्रमागत अर्धवृत्तों से बने इस सर्पिल की कुल लम्बाई क्या है? $(\pi=\frac{22}{7} = 227$ लीजिए।$)$View Solution
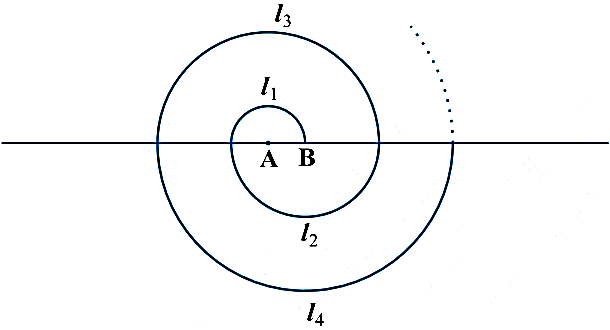
$[$संकेत: क्रमश: केंद्रों $A, B, A, B, ...$ वाले अर्धवृत्तों की लंबाइयाँ $l_1, l_2, l_3, l_4$ हैं।$]$ - 4निम्नलिखित सारणी में, रिक्त स्थानों को भरिए, जहाँ $A.P.$ का प्रथम पद $a,$ सार्व अंतर $d$ और $n$वाँ पद $a_n$ है:View Solution
$
$$a$ $d$ $n$ $a_n$ $i$ $7$ $3$ $8$ $...$ $ii$ $-18$ $...$ $10$ $0$ $iii$ $...$ $-3$ $18$ $-5$ $iv$ $-18.9$ $2.5$ $...$ $3.6$ $v$ $3.5$ $0$ $105$ $...$ - 5$200$ लट्ठों $($logs$)$ को ढेरी के रूप में इस प्रकार रखा जाता है : सबसे नीचे वाली पंक्ति में $20$ लट्टे, उससे अगली पंक्ति में $19$ लट्ठे, उससे अगली पंक्ति में $18$ लट्ठे इत्यादि $($देखिए संलग्न आकृति$)$। ये $200$ लट्ठे कितनी पंक्तियों में रखे गये हैं तथा सबसे ऊपरी पंक्ति में कितने लट्ठे हैं?View Solution

- 6एक पंक्ति के मकानों को क्रमागत रूप से $1$ से $49$ तक अंकित किया गया है। दर्शाइए कि $x$ का एक ऐसा मान है कि $x$ से अंकित मकान से पहले के मकानों की संख्याओं का योग उसके बाद वाले मकानों की संख्याओं के योग के बराबर है। $x$ का मान ज्ञात कीजिए।View Solution
- 7किसी $A.P.$ के चौथे और 8वें पदों का योग $24$ है तथा छठे और $10$वें पदों का योग $44$ है। इस $A.P.$ के प्रथम तीन पद ज्ञात कीजिए।View Solution
- 8एक स्कूल के विद्यार्थियों ने वायु प्रदूषण कम करने के लिए स्कूल के अंदर और बाहर पेड़ लगाने के बारे में सोचा। यह निर्णय लिया गया कि प्रत्येक कक्षा का प्रत्येक अनुभाग अपनी कक्षा की संख्या के बराबर पेड़ लगाएगा। उदाहरणार्थ, कक्षा I का एक अनुभाग पेड़ लगाएगा, कक्षा $II$ का एक अनुभाग $2$ पेड़ लगाएगा, कक्षा $II$ का एक अनुभाग $3$ पेड़ लगाएगा, इत्यादि और ऐसा कक्षा $XII$ तक के लिए चलता रहेगा। प्रत्येक कक्षा के तीन अनुभाग हैं। इस स्कूल के विद्यार्थियों द्वारा लगाए गए कुल पेड़ों की संख्या कितनी होगी?View Solution
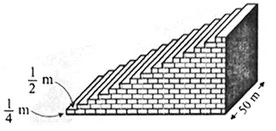
- 9एक फुटबॉल के मैदान में एक छोटा चबूतरा है, जिसमें $15$ सीढ़ियाँ बनी हुई हैं। इन सीढ़ियों में से प्रत्येक की लम्बाई $50 m$ है और वह ठोस कंक्रीट $($Concrete$)$ की बनी है। प्रत्येक सीढ़ी में $\frac{1}{4} m$ की चढ़ाई है और $\frac{1}{2} m$ का फैलाव $($चौड़ाई$)$ है $($देखिए आकृति$)$। इस चबूतरे को बनाने में लगी कुल कंक्रीट का आयतन परिकलित कीजिए।View Solution
$[$संकेत: पहली सीढ़ी को बनाने में लगी कंक्रीट का आयतन $=\frac{1}{4} \times \frac{1}{2} \times 50 \mathrm{~m}^{3}$ है।]