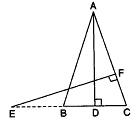
एक त्रिभुज ABC की भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं। दर्शाइए कि$\triangle$ABC$\sim$$\triangle$PQR है।
Exercise-6.3-14
दो त्रिभुजों ABC और PQR में,
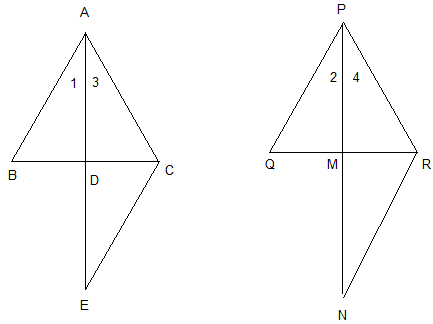
AD और PM क्रमशः भुजाओं BC और QR के संगत माध्यिकाएँ हैं।
$\frac{{AB}}{{PQ}}=\frac{\frac{1}{2} {AC}}{\frac{1}{2} {PR}}=\frac{{AD}}{{PM}}$
$\Rightarrow$ $\frac{{AB}}{{PQ}}=\frac{{BD}}{{QM}}=\frac{{AD}}{{PM}}$
$\Rightarrow$$\frac{{AB}}{{PQ}}=\frac{{AC}}{{PR}}=\frac{{AD}}{{PM}}$ ...(i)
$\Rightarrow$$\triangle$ABD$\sim$$\triangle$PQM ...[SSS समरूपता कसौटी से]
चूंकि समरूप त्रिभुजों के संगत कोण समान होते हैं
$\therefore$$\angle$ ABD =$\angle$PQM
$\Rightarrow$$\angle$ABC =$\angle$PQR ...(ii)
अब,$\triangle$ABC और$\triangle$PQR में,
$\because$$\angle$ABC =$\angle$PQR ...[(ii) से]
तथा$\frac{{AB}}{{PQ}}=\frac{{BC}}{{QR}}$ ...[(i) से]
$\therefore$ SAS समरूपता कसौटी से,
$\triangle$ABC$\sim$$\triangle$PQR

AD और PM क्रमशः भुजाओं BC और QR के संगत माध्यिकाएँ हैं।
$\frac{{AB}}{{PQ}}=\frac{\frac{1}{2} {AC}}{\frac{1}{2} {PR}}=\frac{{AD}}{{PM}}$
$\Rightarrow$ $\frac{{AB}}{{PQ}}=\frac{{BD}}{{QM}}=\frac{{AD}}{{PM}}$
$\Rightarrow$$\frac{{AB}}{{PQ}}=\frac{{AC}}{{PR}}=\frac{{AD}}{{PM}}$ ...(i)
$\Rightarrow$$\triangle$ABD$\sim$$\triangle$PQM ...[SSS समरूपता कसौटी से]
चूंकि समरूप त्रिभुजों के संगत कोण समान होते हैं
$\therefore$$\angle$ ABD =$\angle$PQM
$\Rightarrow$$\angle$ABC =$\angle$PQR ...(ii)
अब,$\triangle$ABC और$\triangle$PQR में,
$\because$$\angle$ABC =$\angle$PQR ...[(ii) से]
तथा$\frac{{AB}}{{PQ}}=\frac{{BC}}{{QR}}$ ...[(i) से]
$\therefore$ SAS समरूपता कसौटी से,
$\triangle$ABC$\sim$$\triangle$PQR
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1आकृति में,$\triangle ABC$ के शीर्षलंब $AD$ और $CE$ परस्पर बिंदु $P$ पर प्रतिच्छेद करते हैं तो दर्शाइए कि: $\triangle AEP\sim \triangle ADB$View Solution
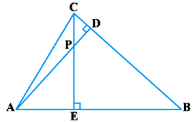
- 2समान्तर चतुर्भुज ABCD की बढाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है। दर्शाइए कि$\triangle$ABE$\sim$$\triangle$CFB है।View Solution
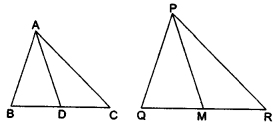
- 3एक त्रिभुज ABC कि भुजाएँ AB और BC तथा माध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ और QR तथा माध्यिका PM के समानुपाती हैं (आकृति देखिए)| दर्शाइए कि$\triangle$ABC$\sim$$\triangle$PQR है|View Solution
- 4एक त्रिभुज $\text{ABC}$ की भुजा $BC$ पर एक बिन्दु $D$ इस प्रकार स्थित है कि $\angle ADC =\angle BAC$ है। दर्शाइए कि $CA^2 =CB \cdot CD$ है।View Solution
- 5AD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं, जबकि$\triangle$ABC$\sim$$\triangle$PQR है। सिद्ध कीजिए कि $\frac{AB}{PQ} = \frac{AD}{PM}$ है।View Solution
- 6आकृति में, $\text{ABC}$ और $\text{AMP}$ दो समकोण त्रिभुज है, जिसके कोण $B$ और $M$ समकोण हैं। सिद्ध कीजिए कि:View Solution
- $\triangle ABC \sim \triangle AMP$
- $\frac{CA}{PA} = \frac{BC}{MP}$
- 7लंबाई $6 m$ वाले एक उध्वार्धर स्तम्भ की भूमि पर छाया की लंबाई $4 m$ है, जबकि उसी समय एक मीनार की छाया की लंबाई $28 m$ है। मीनार की ऊँचाई ज्ञात कीजिए।View Solution
- 8आकृति में,$\triangle ABC$ के शीर्षलंब $AD$ और $CE$ परस्पर बिंदु $P$ पर प्रतिच्छेद करते हैं तो दर्शाइए कि: $\triangle PDC \sim\triangle BEC$View Solution

- 9आकृति में, $AB = AC$ वाले, एक समद्विबाहु त्रिभुज $\text{ABC}$ की बढाई गई भुजा $CB$ पर स्थित $E$ एक बिन्दु है। यदि $AD\perp BC$ और $EF\perp AC$ है तो सिद्ध कीजिए कि$\triangle \text{ABD}\sim\triangle \text{ECF}$ है।View Solution