एक त्रिभुज की भुजाओं की दिक् $-$ कोसाइन ज्ञात कीजिए यदि त्रिभुज के शीर्ष बिंदु $(3, 5, -4), (-1, 1, 2)$ और $(-5, -5, -2)$ हैं।
Exercise-11.1-5
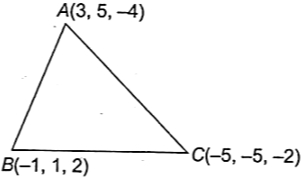
माना त्रिभुज के शीर्ष बिंदु क्रमशः $A(3, 5, -4), B(-1, 1, 2)$ तथा $C(-5, -5, -2)$ हैं।
भुजा $AB$ के दिक् अनुपात निम्न हैं, $[-1 - 3, 1 - 5, 2 - (-4)] = (-4, -4, 2 + 4)$ अर्थात् $(-4, -4, 6) [\because$ यदि बिंदु $A(x_1, y_1, z_1)$ तथा $B(x_2, y_2, z_2)$ हैं, तो रेखा $AB$ का दिक् अनुपात $= (x_2 - x_1, y_2 - y_1, z_2 - z_1)]$
$AB$ का परिमाण,
$|AB| = \sqrt{(-4)^{2}+(-4)^{2}+(6)^{2}}$
$=\sqrt{16+16+36}=\sqrt{68}=2 \sqrt{17}$
अतः $AB$ की दिक् $-$ कोसाइन निम्न हैं,
$\frac{-4}{2 \sqrt{17}}, \frac{-4}{2 \sqrt{17}}, \frac{6}{2 \sqrt{17}}$
$\Rightarrow \frac{-2}{\sqrt{17}}, \frac{-2}{\sqrt{17}}, \frac{3}{\sqrt{17}} [\because$ यदि $a, b,$ व $c$ क्रमशः दिक अनुपात हैं,$]$
तो दिक्-कोसाइन निम्न होंगी $\frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}, \frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}, \frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}}]$
इसी प्रकार, $BC$ भुजा के दिक् अनुषात निम्न हैं, $[-5 - (-1)], (-5 - 1)$ तथा $(-2 - 2)$ अर्थात् $(-4, -6, -4)]$
$BC$ का परिमाण, $|BC| = \sqrt{(-4)^{2}+(-6)^{2}+(-4)^{2}}=\sqrt{68}=2 \sqrt{17}$
अतः $BC$ की दिक् $-$ कोसाइन निम्न हैं,
$\frac{-4}{2 \sqrt{17}}, \frac{-6}{2 \sqrt{17}}, \frac{-4}{2 \sqrt{17}} \Rightarrow \frac{-2}{\sqrt{17}}, \frac{-3}{\sqrt{17}}, \frac{-2}{\sqrt{17}}$
भुजा $CA$ के दिक् अनुपात निम्न हैं, $(-5 -3), (-5 -5)$ तथा $[-2 - (-4)] $अथीत् $(-8, -10, 2)$ या $(8, 10, -2)$
$|CA| = \sqrt{(-8)^{2}+(-10)^{2}+(2)^{2}}$
$=\sqrt{64+100+4}=\sqrt{168}=2 \sqrt{42}$
$AC$ की दिक् $-$ कोसाइन निम्न हैं, $\frac{8}{2 \sqrt{42}}, \frac{10}{2 \sqrt{42}}, \frac{-2}{2 \sqrt{42}} \Rightarrow \frac{4}{\sqrt{42}}, \frac{5}{\sqrt{42}}, \frac{-1}{\sqrt{42}}$
भुजा $AB$ के दिक् अनुपात निम्न हैं, $[-1 - 3, 1 - 5, 2 - (-4)] = (-4, -4, 2 + 4)$ अर्थात् $(-4, -4, 6) [\because$ यदि बिंदु $A(x_1, y_1, z_1)$ तथा $B(x_2, y_2, z_2)$ हैं, तो रेखा $AB$ का दिक् अनुपात $= (x_2 - x_1, y_2 - y_1, z_2 - z_1)]$

$AB$ का परिमाण,
$|AB| = \sqrt{(-4)^{2}+(-4)^{2}+(6)^{2}}$
$=\sqrt{16+16+36}=\sqrt{68}=2 \sqrt{17}$
अतः $AB$ की दिक् $-$ कोसाइन निम्न हैं,
$\frac{-4}{2 \sqrt{17}}, \frac{-4}{2 \sqrt{17}}, \frac{6}{2 \sqrt{17}}$
$\Rightarrow \frac{-2}{\sqrt{17}}, \frac{-2}{\sqrt{17}}, \frac{3}{\sqrt{17}} [\because$ यदि $a, b,$ व $c$ क्रमशः दिक अनुपात हैं,$]$
तो दिक्-कोसाइन निम्न होंगी $\frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}, \frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}, \frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}}]$
इसी प्रकार, $BC$ भुजा के दिक् अनुषात निम्न हैं, $[-5 - (-1)], (-5 - 1)$ तथा $(-2 - 2)$ अर्थात् $(-4, -6, -4)]$
$BC$ का परिमाण, $|BC| = \sqrt{(-4)^{2}+(-6)^{2}+(-4)^{2}}=\sqrt{68}=2 \sqrt{17}$
अतः $BC$ की दिक् $-$ कोसाइन निम्न हैं,
$\frac{-4}{2 \sqrt{17}}, \frac{-6}{2 \sqrt{17}}, \frac{-4}{2 \sqrt{17}} \Rightarrow \frac{-2}{\sqrt{17}}, \frac{-3}{\sqrt{17}}, \frac{-2}{\sqrt{17}}$
भुजा $CA$ के दिक् अनुपात निम्न हैं, $(-5 -3), (-5 -5)$ तथा $[-2 - (-4)] $अथीत् $(-8, -10, 2)$ या $(8, 10, -2)$
$|CA| = \sqrt{(-8)^{2}+(-10)^{2}+(2)^{2}}$
$=\sqrt{64+100+4}=\sqrt{168}=2 \sqrt{42}$
$AC$ की दिक् $-$ कोसाइन निम्न हैं, $\frac{8}{2 \sqrt{42}}, \frac{10}{2 \sqrt{42}}, \frac{-2}{2 \sqrt{42}} \Rightarrow \frac{4}{\sqrt{42}}, \frac{5}{\sqrt{42}}, \frac{-1}{\sqrt{42}}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1समतल $\vec{r} \cdot(6 \hat{i}-3 \hat{j}-2 \hat{k})$ + 1 = 0 पर मूल बिंदु से डाले गए लंब इकाई सदिश की दिक्-कोसाइन ज्ञात कीजिए।View Solution
- 2समतलों $\vec{r} \cdot(\hat{i}+\hat{j}+\hat{k}) = 6$ और $\vec{r} \cdot(2 \hat{i}+3 \hat{j}+4 \hat{k}) = -5,$ के प्रतिच्छेदन तथा बिंदु $(1, 1, 1)$ से जाने वाले समतल का सदिश समीकरण ज्ञात कीजिए।View Solution
- 3उस समतल का सदिश समीकरण ज्ञात कीजिए जो समतलों $\vec{r} \cdot(2 \hat{i}+2 \hat{j}-3 \hat{k})$ = 7, $\vec{r} \cdot(2 \hat{i}+5 \hat{j}+3 \hat{k})$ = 9 के प्रतिच्छेदन रेखा और (2, 1, 3) से होकर जाता है।View Solution
- 4समतलों $\vec{r} \cdot(\hat{i}+\hat{j}+\hat{k})$ = 1 और $\vec{r} \cdot(2 \hat{i}+3 \hat{j}-\hat{k})$ + 4 = 0 के प्रतिच्छेदन रेखा से जाने वाले तथा x-अक्ष के समांतर तल का समीकरण ज्ञात कीजिए।View Solution
- 5समतलों $\vec{r} \cdot(\hat{i}+2 \hat{j}+3 \hat{k})$ - 4 = 0 और $\vec{r} \cdot(2 \hat{i}+\hat{j}-\hat{k})$ + 5 = 0 के प्रतिच्छेदन रेखा को अंतर्विष्ट करने वाले तथा तल $\vec{r} \cdot(5 \hat{i}+3 \hat{j}-6 \hat{k})$ + 8 = 0 के लंबवत् तल का समीकरण ज्ञात कीजिए।View Solution
- 6एक रेखा, एक घन के विकर्णों के साथ $\alpha, \beta, \gamma, \delta,$ कोण बनाती है तो सिद्ध कीजिए कि $\cos^2 \alpha + \cos^2\beta + \cos^2 \gamma + \cos^2 \delta = \frac{4}{3}$View Solution
- 7View Solutionउस बिंदु के निर्देशांक ज्ञात कीजिए जहाँ बिंदुओं (5, 1, 6) और (3, 4, 1) को मिलाने वाली रेखा YZ-तल को काटती है।
- 8रेखाओं l_1 और l_2 के बीच की न्यूनतम दूरी ज्ञात कीजिए जिनके सदिश समीकरण है: $\vec{r}=\hat{i}+\hat{j}+\lambda(2 \hat{i}-\hat{j}+\hat{k}) ...(i)$ और $\vec{r}=2 \hat{i}+\hat{j}-\hat{k}+\mu(3 \hat{i}-5 \hat{j}+2 \hat{k}) ...(ii)$View Solution
- 9बिंदु (5, 2, -4) से जाने वाली तथा सदिश $3 \hat{i}+2 \hat{j}-8 \hat{k}$ के समांतर रेखा का सदिश तथा कार्तीय समीकरणों को ज्ञात कीजिए।View Solution
- 10View Solutionउस बिंदु के निर्देशांक ज्ञात कीजिए जहाँ बिंदुओं A(3, 4, 1) और B(5, 1, 6) को मिलाने वाली रेखा XY-तल को काटती हैं।
