(आहार संबंधी समस्या): एक आहार विज्ञानी दो प्रकार के भोज्यों को इस प्रकार मिलाना चाहता है कि मिश्रण में विटामिन A का घटक कम से कम 8 मात्रक और विटामिन C का घटक कम से कम 10 मात्रक हो। भोज्य I में 2 मात्रक विटामिन A प्रति kg और 1 मात्रक विटामिन C प्रति kg है। जबकि भोज्य II में 1 मात्रक विटामिन A प्रति kg और 2 मात्रक विटामिन C प्रति kg है। दिया है कि प्रति kg भोज्य I को खरीदने में ₹50 और प्रति kg भोज्य II को खरीदने में ₹70 लगते हैं। इस प्रकार के भोज्य मिश्रण का न्यूनतम मूल्य ज्ञात कीजिए।
example-6
Download our app for free and get started
माना कि मिश्रण में भोज्य I का x kg और भोज्य II का y kg है। स्पष्टतः x $\geq$ 0 y $\geq$ 0. हम प्रदत्त आँकड़ों से निम्न सारणी बनाते हैं।
| स्रोत | भोज्य पदार्थ | आवश्यकता (मात्रकों में) | |
| I (x) | II (y) | ||
| विटामिन A (मात्रक/ kg) | 2 | 1 | 8 |
| विटामिन C (मात्रक/kg) | 1 | 2 | 10 |
| लागत (₹/kg) | 50 | 70 | |
चूँकि मिश्रण में विटामिन A की कम से कम 8 मात्रक और विटामिन C के 10 मात्रक होने चाहिए, अतः निम्नलिखित व्यवरोध प्राप्त होते हैं
2x + y $\geq$ 8
x + 2y $\geq$ 10
भोज्य I के x kg और भोज्य II के y kg खरीदने का कुल मूल्य Z है जहाँ
Z = 50x + 70y
अतः समस्या का गणितीय सूत्रीकरण निम्नलिखित है:
निम्न व्यवरोधों के अंतर्गत
2x + y $\geq$ 8 ...(i)
x + 2y $\geq$ 10 ...(ii)
x, y $\geq$ 0 ...(iii)
Z = 50x + 70y का न्यूनतमीकरण कीजिए
असमीकरणों (i) से (iii) तक के आलेखों द्वारा निर्धारित सुसंगत क्षेत्र को आकृति में दिखाया गया है।
| कोनीय बिंदु | Z = 50x + 70y |
| (0, 8) | 560 |
| (2, 4) | 380 $\leftarrow$ न्यूनतम |
| (10, 0) | 500 |
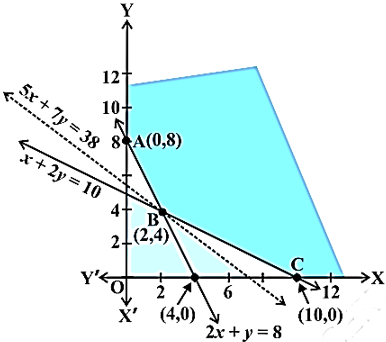
यहाँ हम देखते हैं कि सुसंगत क्षेत्र अपरिबद्ध है।
हमें कोनीय बिंदुओं A(0, 8), B(2, 4) और C(10, 0) पर Z का मान ज्ञात करना है।
सारणी में, बिंदु (2, 4) पर Z का सबसे कम मान 380 है, क्या हम कह सकते हैं कि Z का न्यूनतम मान 380 है (क्यों?) याद कीजिए कि सुसंगत क्षेत्र अपरिबद्ध है। इसलिए हमें निम्नलिखित असमीकरण का आलेख खींचना पड़ेगा।
50x + 70y < 380
अर्थात् 5x + 7y < 38
जाँच करने के लिए कि क्या असमीकरण द्वारा निर्धारित परिणामी खुला अर्धतल, सुसंगत क्षेत्र के साथ कोई उभयनिष्ठ बिंदु रखता है। आकृति में हम देखते हैं कि यहाँ कोई उभयनिष्ठ बिंदु नहीं है।
अतः, बिंदु (2, 4) पर Z का प्राप्त न्यूनतम मान 380 है। इसलिए आहार विज्ञानी की इष्टतम मिश्रण योजना भोज्य 'I' की 2 kg और भोज्य 'II' के 4 kg के मिश्रण बनाने की हो सकती है और इस योजना के अंतर्गत मिश्रण का न्यूनतम मूल्य ₹ 380 होगा।
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionएक फल उत्पादक अपने बाग में दो प्रकार के खादों P ब्रांड और Q ब्रांड का उपयोग कर सकता है। मिश्रण के प्रत्येक थैले में नाइट्रोजन, फास्फोरिक अम्ल, पोटाश और क्लोरीन की मात्रा (kg में) सारणी में दिया गया है। परीक्षण संकेत देते है कि बाग को कम से कम 250 kg फास्फोरिक अम्ल, कम से कम 270 kg पोटाश और क्लोरीन की अधिक से अधिक 310 kg की आवश्यकता है।
यदि उत्पादक बाग के लिए मिलाई जाने वाली नाइट्रोजन की मात्रा का न्यूनतमीकरण करना चाहता है तथा, प्रत्येक मिश्रण के कितने थैलों का उपयोग होना चाहिए? मिलाई जाने वाली नाइट्रोजन की निम्नतम मात्रा क्या है?
kg प्रति थैला ब्राँड P ब्राँड Q नाइट्रोजन 3 3.5 फास्फोरिक अम्ल 1 2 पोटाश 3 1.5 क्लोरीन 1.5 2 - 2एक भोज्य पदार्थ में कम से कम $80$ मात्रक विटामिन $A$ और $100$ मात्रक खनिज होना चाहिए। दो प्रकार के भोज्य $F_1$ और $F_2$ उपलब्ध हैं। भोज्य $F_1$ की लागत $₹\ 4$प्रति मात्रक और $F_2$ की लागत $₹\ 5$ प्रति मात्रक है। भोज्य $F_1$ की एक इकाई में कम से कम $3$ मात्रक विटामिन $A$ और $4$ मात्रक खनिज है। $F_2$ की प्रति इकाई में कम से कम $6$ मात्रक विटामिन $A$ और $3$ मात्रक खनिज हैं। इसको एक रैखिक प्रोग्रामन समस्या के रूप में सूत्रबद्ध कीजिए। उस आहार का न्यूनतम मूल्य ज्ञात कीजिए, जिसमें इन दो भोज्यों का मिश्रण है और उसमें न्यूनतम पोषक तत्व हैं।View Solution
- 3दिखाइए कि Z का न्यूनतम मान दो बिंदुओं से अधिक बिंदुओं पर घटित होता है।View Solution
निम्न अवरोधों के अंतर्गत Z = x + 2y का न्यूनतमीकरण तथा अधिकतमीकरण कीजिए:
x + 2y $\geq$ 100, 2x - y $\leq$ 0, 2x + y $\leq$ 200; x, y $\geq$ 0 - 4View Solutionउत्पादन संबंधी समस्या (Manufacturing Problem) एक निर्माणकर्ता कंपनी एक उत्पाद के दो नमूने (प्रतिमान) A और B बनाती है। नमूना A के प्रत्येक नग बनाने के लिए 9 श्रम घंटे और 1 घंटा पॉलिश करने के लिए लगता है जबकि नमूना B के प्रत्येक नग के बनाने में 12 श्रम घंटे तथा पॉलिश करने में 3 श्रम घटों की आवश्यकता होती है। बनाने तथा पॉलिश करने के लिए उपलब्ध अधिकतम श्रम घंटे क्रमशः 180 तथा 30 हैं। कंपनी नमूना A के प्रत्येक नग पर ₹ 8000 तथा नमूना B के प्रत्येक नग पर ₹12000 का लाभ कमाती है। नमूना A और नमूना B के कितने नगों का अधिकतम लाभ कमाने के लिए प्रति सप्ताह निर्माण करना चाहिए? प्रति सप्ताह अधिकतम लाभ क्या है?
- 5View Solutionएक उत्पादन के कारखाने में तीन मशीनें I, II और III लगी हैं। मशीनें I और II अधिकतम 12 घंटे तक चलाए जाने की क्षमता रखती है। जबकि मशीन III प्रतिदिन कम से कम 5 घंटे चलना चाहिए। निर्माणकर्ता केवल दो प्रकार के सामान M और N का उत्पादन करता है, जिनमें प्रत्येक के उत्पादन में तीनों मशीनों की आवश्यकता होती है। M और N के प्रत्येक उत्पाद के एक नग उत्पादन में तीनों मशीनों के संगत लगे समय (घंटों में) निम्न लिखित सारणी में दिए हैं।
उत्पाद मशीन पर लगा समय (घंटों में) I II III M 1 2 1 N 2 1 1.25 वह उत्पाद M पर ₹600 प्रति नग और उत्पाद N पर ₹400 प्रति नग की दर से लाभ कमाती है। मानते हुए कि उसके सभी उत्पाद बिक जाते हैं, जिनका उत्पादन किया गया है, तब ज्ञात कीजिए कि प्रत्येक उत्पाद के कितने नगों का उत्पादन किया जाए, जिससे लाभ का अधिकतमीकरण हो? अधिकतम लाभ क्या होगा?
- 6आलेखीय विधि द्वारा उद्देश्य फलन Z = -50x + 20y का न्यूनतम मान निम्नलिखित व्यवरोधों के अंतर्गत ज्ञात कीजिए:View Solution
2x - y $\geq$ -5 ...(i)
3x + y $\geq$ 3 ...(ii)
2x - 3y $\leq$ 12 ...(iii)
x $\geq$ 0, y $\geq$ 0 ...(iv) - 7ग्राफ़ीय विधि से रैखिक प्रोग्रामन समस्या को हल कीजिए:View Solution
निम्न अवरोधों के अंतर्गत Z = 3x + 2y का न्यूनतमीकरण कीजिए:
x + 2y $\leq$ 10, 3x + y $\leq$ 15, x, y $\geq$ 0 - 8View Solution(आहार समस्या) एक आहारविद् दो भोज्यों P और Q का उपयोग करते हुए एक विशेष आहार तैयार करता है। भोज्य P का प्रत्येक पैकेट (जिसमें 30 ग्राम अंतर्विष्ट है) में कैल्शियम के 12 मात्रक लौह तत्व के 4 मात्रक, कोलेस्ट्रोल के 6 मात्रक और विटामिन A के 6 मात्रक अंतर्विष्ट हैं जबकि उसी मात्र के भोज्य Q के पैकेट में कैल्शियम तत्व के 3 मात्रक, लौह तत्व के 20 मात्रक, कोलेस्ट्रोल के 4 मात्रक और विटामिन A के 3 मात्रक अंतर्विष्ट है। आहार में कम से कम 240 मात्रक कैल्शियम, लौह तत्व के कम से कम 460 मात्रक, और कोलेस्ट्रोल के अधिक से अधिक 300 मात्रक अपेक्षित हैं। प्रत्येक भोज्य के कितने पैकेटों का उपयोग किया जाए ताकि आहार में विटामिन A की मात्रा का न्यूनतम किया जा सके।
- 9View Solutionएक हवाई जहाज अधिकतम 200 यात्रियों को यात्रा करा सकता है। प्रत्येक प्रथम श्रेणी के टिकट पर ₹1000 और सस्ते श्रेणी के टिकट पर ₹600 का लाभ कमाया जा सकता है। एयरलाइन कम से कम 20 सीटें प्रथम श्रेणी के लिए आरक्षित करती है। तथापि प्रथम श्रेणी की अपेक्षा कम से कम 4 गुने यात्री सस्ती श्रेणी के टिकट से यात्रा करने को वरीयता देते हैं। ज्ञात कीजिए कि प्रत्येक प्रकार के कितने-कितने टिकट बेचे जाएँ ताकि लाभ का अधिकतमीकरण हो? अधिकतम लाभ कितना है?
- 10ग्राफ़ीय विधि से रैखिक प्रोग्रामन समस्या को हल कीजिए:View Solution
निम्न अवरोधों के अंतर्गत Z = x + 2y का न्यूनतमीकरण कीजिए:
2x + y $\geq$ 3, x + 2y $\geq$ 6, x, y $\geq$ 0