उत्पादन संबंधी समस्या (Manufacturing Problem) एक निर्माणकर्ता कंपनी एक उत्पाद के दो नमूने (प्रतिमान) A और B बनाती है। नमूना A के प्रत्येक नग बनाने के लिए 9 श्रम घंटे और 1 घंटा पॉलिश करने के लिए लगता है जबकि नमूना B के प्रत्येक नग के बनाने में 12 श्रम घंटे तथा पॉलिश करने में 3 श्रम घटों की आवश्यकता होती है। बनाने तथा पॉलिश करने के लिए उपलब्ध अधिकतम श्रम घंटे क्रमशः 180 तथा 30 हैं। कंपनी नमूना A के प्रत्येक नग पर ₹ 8000 तथा नमूना B के प्रत्येक नग पर ₹12000 का लाभ कमाती है। नमूना A और नमूना B के कितने नगों का अधिकतम लाभ कमाने के लिए प्रति सप्ताह निर्माण करना चाहिए? प्रति सप्ताह अधिकतम लाभ क्या है?
example-8
मान लीजिए कि नमूना A के नगों की संख्या x है तथा नमूना B के नगों की संख्या y है।
इसलिए कुल लाभ = (₹8000x + 12000y)
अतः Z = 8000x + 12000y
अब हमारे पास प्रदत्त समस्या का गणितीय सूत्रीकरण निम्नलिखित है:
निम्न व्यवरोधों के अंतर्गत
9x + 12y $\leq$ 180
अर्थात् 3x + 4y $\leq$ 60 (गढ़ने का व्यवरोध) ...(i)
x + 3y $\leq$ 30 (पॉलिश का व्यवरोध) ...(ii)
x $\geq$ 0, y $\geq$ 0 (ऋणेतर व्यवरोध) ...(iii)
Z = 8000x + 12000y का अधिकतमीकरण कीजिए।
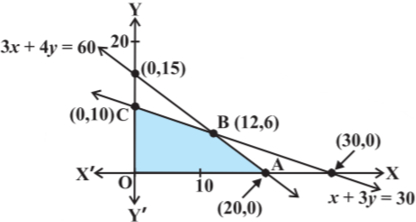
रैखिक असमीकरण (i) से (iii) द्वारा निर्धारित सुसंगत क्षेत्र OABC (छायांकित) आकृति में दिखाया गया है। ध्यान दीजिए कि सुसंगत क्षेत्र परिबद्ध है।
प्रत्येक कोनीय बिंदु पर उद्देश्य फलन Z का मान की गणना की गई है जैसा कि निम्न सारणी में दिखाया गया है:
इसलिए कुल लाभ = (₹8000x + 12000y)
अतः Z = 8000x + 12000y
अब हमारे पास प्रदत्त समस्या का गणितीय सूत्रीकरण निम्नलिखित है:
निम्न व्यवरोधों के अंतर्गत
9x + 12y $\leq$ 180
अर्थात् 3x + 4y $\leq$ 60 (गढ़ने का व्यवरोध) ...(i)
x + 3y $\leq$ 30 (पॉलिश का व्यवरोध) ...(ii)
x $\geq$ 0, y $\geq$ 0 (ऋणेतर व्यवरोध) ...(iii)
Z = 8000x + 12000y का अधिकतमीकरण कीजिए।
रैखिक असमीकरण (i) से (iii) द्वारा निर्धारित सुसंगत क्षेत्र OABC (छायांकित) आकृति में दिखाया गया है। ध्यान दीजिए कि सुसंगत क्षेत्र परिबद्ध है।

प्रत्येक कोनीय बिंदु पर उद्देश्य फलन Z का मान की गणना की गई है जैसा कि निम्न सारणी में दिखाया गया है:
| कोनीय बिंदु | Z = 8000x + 12000y |
| O(0, 0) | 0 |
| A(20, 0) | 160000 |
| B(12, 6) | 168000 $\leftarrow$ अधिकतम |
| C(0, 10) | 120000 |
हम शीर्ष B (12, 6) पर Z का अधिकतम मान ₹1,68,000 पाते हैं। अतः कंपनी को नमूना A के 12 नग तथा नमूना B के 6 नगों के उत्पादन पर अधिकतम लाभ कमाने के लिए करना चाहिए और अधिकतम लाभ ₹1,68,000 होगा।
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1आलेखीय विधि द्वारा उद्देश्य फलन Z = -50x + 20y का न्यूनतम मान निम्नलिखित व्यवरोधों के अंतर्गत ज्ञात कीजिए:View Solution
2x - y $\geq$ -5 ...(i)
3x + y $\geq$ 3 ...(ii)
2x - 3y $\leq$ 12 ...(iii)
x $\geq$ 0, y $\geq$ 0 ...(iv) - 2View Solution(आहार समस्या) एक आहारविद् दो भोज्यों P और Q का उपयोग करते हुए एक विशेष आहार तैयार करता है। भोज्य P का प्रत्येक पैकेट (जिसमें 30 ग्राम अंतर्विष्ट है) में कैल्शियम के 12 मात्रक लौह तत्व के 4 मात्रक, कोलेस्ट्रोल के 6 मात्रक और विटामिन A के 6 मात्रक अंतर्विष्ट हैं जबकि उसी मात्र के भोज्य Q के पैकेट में कैल्शियम तत्व के 3 मात्रक, लौह तत्व के 20 मात्रक, कोलेस्ट्रोल के 4 मात्रक और विटामिन A के 3 मात्रक अंतर्विष्ट है। आहार में कम से कम 240 मात्रक कैल्शियम, लौह तत्व के कम से कम 460 मात्रक, और कोलेस्ट्रोल के अधिक से अधिक 300 मात्रक अपेक्षित हैं। प्रत्येक भोज्य के कितने पैकेटों का उपयोग किया जाए ताकि आहार में विटामिन A की मात्रा का न्यूनतम किया जा सके।
- 3View Solutionएक निर्माता दो प्रकार के खिलौने A और B बनाता है। इस उद्देश्य के लिए निर्माण में तीन मशीनों की आवश्यकता पड़ती है और प्रत्येक प्रकार के खिलौने के निर्माण के लिए लगा समय (मिनटों में) निम्नलिखित है।
खिलौने के प्रकार मशीन I II III A 12 18 6 B 6 0 9 प्रत्येक मशीन अधिकतम 6 घंटे प्रतिदिन के लिए उपलब्ध है। यदि A प्रकार के खिलौने की बिक्री पर ₹7.50 लाभ और B प्रकार के खिलौने पर ₹5 का लाभ हो तो दर्शाइए कि अधिकतम लाभ कमाने के लिए प्रतिदिन A प्रकार के 15 खिलौने और B प्रकार 30 खिलौने निर्मित होने चाहिए।
- 4View Solutionपरिवहन संबंधी समस्या (Transportation Problem) P और Q दो स्थानों पर दो कारखाने स्थापित हैं। इन स्थानों से सामान A, B और C पर स्थित तीन डिपो में भेजे जाते हैं। इन डिपो की साप्ताहिक आवश्यकता क्रमशः 5, 5 और 4 सामान की नग हैं, जब कि P और Q की स्थापित कारखानों की उत्पादन क्षमता 8 और 6 नग हैं।
प्रति नग परिवहन व्यय निम्न सारणीबद्ध है:से/को मूल्य (₹ में) A B C P 160 100 150 Q 100 120 100 प्रत्येक कारखाने से कितने नग सामान प्रत्येक डिपो को भेजा जाए जिससे परिवहन व्यय न्यूनतम हो? न्यूनतम परिवहन व्यय क्या होगा।
- 5ग्राफ़ीय विधि से निम्न रैखिक प्रोग्रामन समस्या को हल कीजिए:View Solution
निम्न अवरोधों के अंतर्गत Z = 5x + 3y का अधिकतमीकरण कीजिए:
3x + 5y $\leq$ 15, 5x + 2y $\leq$ 10, x $\geq$ 0, y $\geq$ 0 - 6View Solutionएक कारखाने में दो प्रकार के पेंच A और B बनते हैं। प्रत्येक के निर्माण में दो मशीनों के प्रयोग की आवश्यकता होती है, जिसमें एक स्वचालित और दूसरी हस्तचालित है। एक पैकेट पेंच A के निर्माण में 4 मिनट स्वचालित और 6 मिनट हस्तचालित मशीन, तथा एक पैकेट पेंच B के निर्माण में 6 मिनट स्वचालित और 3 मिनट हस्तचालित मशीन का कार्य होता है। प्रत्येक मशीन किसी भी दिन के लिए अधिकतम 4 घंटे काम के लिए उपलब्ध है। निर्माता पेंच A के प्रत्येक पैकेट पर ₹7 और पेंच B के प्रत्येक पैकेट पर ₹10 का लाभ कमाता है। यह मानते हुए कि कारखाने में निर्मित सभी पेंचों के पैकेट बिक जाते हैं, ज्ञात कीजिए कि प्रतिदिन कितने पैकेट विभिन्न पेंचों के बनाए जाएँ जिससे लाभ अधिकतम हो तथा अधिकतम लाभ ज्ञात कीजिए।
- 7View Solutionएक फल उत्पादक अपने बाग में दो प्रकार के खादों P ब्रांड और Q ब्रांड का उपयोग कर सकता है। मिश्रण के प्रत्येक थैले में नाइट्रोजन, फास्फोरिक अम्ल, पोटाश और क्लोरीन की मात्रा (kg में) सारणी में दिया गया है। परीक्षण संकेत देते है कि बाग को कम से कम 250 kg फास्फोरिक अम्ल, कम से कम 270 kg पोटाश और क्लोरीन की अधिक से अधिक 310 kg की आवश्यकता है।
यदि उत्पादक बाग के लिए मिलाई जाने वाली नाइट्रोजन की मात्रा का न्यूनतमीकरण करना चाहता है तथा, प्रत्येक मिश्रण के कितने थैलों का उपयोग होना चाहिए? मिलाई जाने वाली नाइट्रोजन की निम्नतम मात्रा क्या है?
kg प्रति थैला ब्राँड P ब्राँड Q नाइट्रोजन 3 3.5 फास्फोरिक अम्ल 1 2 पोटाश 3 1.5 क्लोरीन 1.5 2 - 8ग्राफ़ीय विधि से रैखिक प्रोग्रामन समस्या को हल कीजिए:View Solution
निम्न अवरोधों के अंतर्गत Z = 3x + 2y का न्यूनतमीकरण कीजिए:
x + 2y $\leq$ 10, 3x + y $\leq$ 15, x, y $\geq$ 0 - 9दिखाइए कि Z का न्यूनतम मान दो बिंदुओं से अधिक बिंदुओं पर घटित होता है।View Solution
निम्न अवरोधों के अंतर्गत Z = x + 2y का न्यूनतमीकरण तथा अधिकतमीकरण कीजिए:
x + 2y $\geq$ 100, 2x - y $\leq$ 0, 2x + y $\leq$ 200; x, y $\geq$ 0 - 10ग्राफ़ीय विधि से रैखिक प्रोग्रामन समस्या को हल कीजिए:View Solution
निम्न अवरोधों के अंतर्गत Z = x + 2y का न्यूनतमीकरण कीजिए:
2x + y $\geq$ 3, x + 2y $\geq$ 6, x, y $\geq$ 0
