दो प्रकार के उर्वरक $F_1$ और $F_2$ है। $F_1$ में $10\%$ नाइट्रोजन और $6\%$ फास्फोरिक अम्ल है। तथा $F_2$ में $5\%$ नाइट्रोजन तथा $10\%$ फास्फोरिक अम्ल है। मिट्टी की स्थितिओं का परीक्षण करने के पश्चात् एक किसान पाता है कि उसे अपनी फसल के लिए $14 \ kg$ नाइट्रोजन और $14 \ kg$ फास्फोरिक अम्ल की आवश्यकता है। यदि $F_1$ की कीमत $₹\ 6/ kg$ और $F_2$ की कीमत $₹\ 5/ kg$ है, प्रत्येक प्रकार का कितना उर्वरक उपयोग के लिए चाहिए ताकि न्यूनतम मूल्य पर वांछित पोषक तत्व मिल सके। न्यूनतम लागत क्या है।
Exercise-12.2-10
मान लीजिए किसान उर्वरक $F_1$ का $x$ किग्रा तथा $F_2$ की $y$ किग्रा मात्रा मिलाता है, तब निम्न तालिका प्राप्त होती है।
उर्वरक की कुल लागत, $Z = 6x + 5y$
अतः उद्देश्य फलन $Z = 6x + 5y ...(i)$
का निम्नतम मान निम्न व्यवरोधों के अंतर्गत ज्ञात करना है।
$\frac{x}{10}+\frac{y}{20} \geq 14 \Leftrightarrow 2x + y \geq$ 280 ...(ii)$
तथा $\frac{6 x}{100}+\frac{10 y}{100} \geq14\Leftrightarrow 3x + 5y \geq 700 ...(iii)$
$x \geq 0, y \geq 0 ...(iv)$
सर्वप्रथम, रेखा $2x + y = 280$ का ग्राफ खींचते हैं।
$(0, 0)$ असमिका $2x + y \geq 280$ में रखने पर,
$2 \times 0 + 0 \geq 280 \Rightarrow 0 \geq 280 ($जोकि असत्य है$)$
अतः अर्द्धतल मूलबिंदु की विपरीत ओर होगा। चूँकि $x, y \geq 0$ है, अतः सुसंगत क्षेत्र प्रथम चतुर्थांश में होगा।
अब, रेखा $3x + 5y = 700$ का ग्राफ खींचते हैं।
$(0, 0)$ असमिका $3x + 5y \geq 700$ में रखने पर,
$3 \times 0 + 5 \times 0 \geq 700 \Rightarrow 0 \geq 700 ($जोकि असत्य है$)$
अतः अर्द्धतव मूलबिंदु के विपरीत ओर होगा।
समीकरण $2x + y = 280$ तथा $3x + 5y = 700$ को हल करने पर प्रतिच्छेद बिंदु $B(100, 80)$ प्राप्त होता है।
स्पष्ट है कि सुसंगत क्षेत्र अपरिबद्ध है।
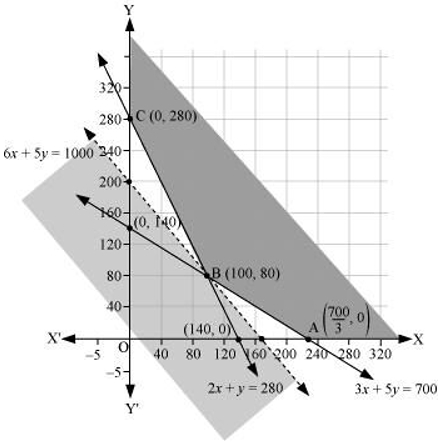
इस प्रकार, सुसंगत क्षेत्र के शीर्ष बिंदु $A\left(\frac{700}{3}, 0\right), B(100, 80)$ तथा $C(0, 280)$ हैं। इन शीर्ष बिंदुओं पर $Z$ का मान निम्न है।
चूँकि सुसंगत क्षेत्र आपरिबद्ध है, अतः $Z$ का निम्नतम मान $100$ हो भी सकता है तथा नहीं भी हो सकता है। इसके लिए असमिका $6x + 5y < 1000$ का ग्राफ खींचते हैं और परीक्षण करते हैं कि प्राप्त अर्द्धतल का कोई बिंदु सुसंगत क्षेत्र में उभयनिष्ठ है या नहीं हैं यहाँ, कोई बिंदु उभयनिष्ठ नहीं है, अतः निम्नतम लागत $₹\ 1000$ प्राप्त करने के लिए उर्वरक $F_1$ के $100$ किग्रा तथा $F_2$ के $80$ किग्रा मात्रा प्रयोग करनी चाहिए।
| प्रकार | मात्रा $($किग्रा में$)$ |
नाइट्रोजन | फास्फोरिक अम्ल |
लागत $(₹$ में$)$ |
| $F_1$ | $x$ | $\frac{10}{100} x=\frac{1}{10} x$ | $\frac{6}{100}$x | $6x$ |
| $F_2$ | $y$ | $\frac{5}{100} y=\frac{1}{20} y$ | $\frac{10}{100}$y | $5y$ |
| कुल | $x + y$ | $\frac{x}{10}+\frac{y}{20}$ | $\frac{6 x}{100}+\frac{10 y}{100}$ | $6x + 5y$ |
| आवश्यकता (किग्रा में) | $14$ | $14$ |
अतः उद्देश्य फलन $Z = 6x + 5y ...(i)$
का निम्नतम मान निम्न व्यवरोधों के अंतर्गत ज्ञात करना है।
$\frac{x}{10}+\frac{y}{20} \geq 14 \Leftrightarrow 2x + y \geq$ 280 ...(ii)$
तथा $\frac{6 x}{100}+\frac{10 y}{100} \geq14\Leftrightarrow 3x + 5y \geq 700 ...(iii)$
$x \geq 0, y \geq 0 ...(iv)$
सर्वप्रथम, रेखा $2x + y = 280$ का ग्राफ खींचते हैं।
| $x$ | $0$ | $140$ |
| $y$ | $280$ | $0$ |
$2 \times 0 + 0 \geq 280 \Rightarrow 0 \geq 280 ($जोकि असत्य है$)$
अतः अर्द्धतल मूलबिंदु की विपरीत ओर होगा। चूँकि $x, y \geq 0$ है, अतः सुसंगत क्षेत्र प्रथम चतुर्थांश में होगा।
अब, रेखा $3x + 5y = 700$ का ग्राफ खींचते हैं।
| $x$ | $0$ | $\frac{700}{3}$ |
| $y$ | $140$ | $0$ |
$3 \times 0 + 5 \times 0 \geq 700 \Rightarrow 0 \geq 700 ($जोकि असत्य है$)$
अतः अर्द्धतव मूलबिंदु के विपरीत ओर होगा।
समीकरण $2x + y = 280$ तथा $3x + 5y = 700$ को हल करने पर प्रतिच्छेद बिंदु $B(100, 80)$ प्राप्त होता है।
स्पष्ट है कि सुसंगत क्षेत्र अपरिबद्ध है।

इस प्रकार, सुसंगत क्षेत्र के शीर्ष बिंदु $A\left(\frac{700}{3}, 0\right), B(100, 80)$ तथा $C(0, 280)$ हैं। इन शीर्ष बिंदुओं पर $Z$ का मान निम्न है।
| शीर्ष बिंदु | $Z = 6x + 5y$ |
| A$\left(\frac{700}{3}, 0\right)$ | $1400$ |
| $B(100, 80)$ | $1000 \rightarrow$ निम्नतम |
| $C(0, 280)$ | $1400$ |
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solution(आहार समस्या) एक आहारविद् दो भोज्यों P और Q का उपयोग करते हुए एक विशेष आहार तैयार करता है। भोज्य P का प्रत्येक पैकेट (जिसमें 30 ग्राम अंतर्विष्ट है) में कैल्शियम के 12 मात्रक लौह तत्व के 4 मात्रक, कोलेस्ट्रोल के 6 मात्रक और विटामिन A के 6 मात्रक अंतर्विष्ट हैं जबकि उसी मात्र के भोज्य Q के पैकेट में कैल्शियम तत्व के 3 मात्रक, लौह तत्व के 20 मात्रक, कोलेस्ट्रोल के 4 मात्रक और विटामिन A के 3 मात्रक अंतर्विष्ट है। आहार में कम से कम 240 मात्रक कैल्शियम, लौह तत्व के कम से कम 460 मात्रक, और कोलेस्ट्रोल के अधिक से अधिक 300 मात्रक अपेक्षित हैं। प्रत्येक भोज्य के कितने पैकेटों का उपयोग किया जाए ताकि आहार में विटामिन A की मात्रा का न्यूनतम किया जा सके।
- 2View Solutionपरिवहन संबंधी समस्या (Transportation Problem) P और Q दो स्थानों पर दो कारखाने स्थापित हैं। इन स्थानों से सामान A, B और C पर स्थित तीन डिपो में भेजे जाते हैं। इन डिपो की साप्ताहिक आवश्यकता क्रमशः 5, 5 और 4 सामान की नग हैं, जब कि P और Q की स्थापित कारखानों की उत्पादन क्षमता 8 और 6 नग हैं।
प्रति नग परिवहन व्यय निम्न सारणीबद्ध है:से/को मूल्य (₹ में) A B C P 160 100 150 Q 100 120 100 प्रत्येक कारखाने से कितने नग सामान प्रत्येक डिपो को भेजा जाए जिससे परिवहन व्यय न्यूनतम हो? न्यूनतम परिवहन व्यय क्या होगा।
- 3दिखाइए कि Z का न्यूनतम मान दो बिंदुओं से अधिक बिंदुओं पर घटित होता है।View Solution
निम्न अवरोधों के अंतर्गत Z = -x + 2y का अधिकतमीकरण कीजिए:
x $\geq$ 3, x + y $\geq$ 5, x + 2y $\geq$ 6, y $\geq$ 0 - 4View Solutionएक निर्माता दो प्रकार के खिलौने A और B बनाता है। इस उद्देश्य के लिए निर्माण में तीन मशीनों की आवश्यकता पड़ती है और प्रत्येक प्रकार के खिलौने के निर्माण के लिए लगा समय (मिनटों में) निम्नलिखित है।
खिलौने के प्रकार मशीन I II III A 12 18 6 B 6 0 9 प्रत्येक मशीन अधिकतम 6 घंटे प्रतिदिन के लिए उपलब्ध है। यदि A प्रकार के खिलौने की बिक्री पर ₹7.50 लाभ और B प्रकार के खिलौने पर ₹5 का लाभ हो तो दर्शाइए कि अधिकतम लाभ कमाने के लिए प्रतिदिन A प्रकार के 15 खिलौने और B प्रकार 30 खिलौने निर्मित होने चाहिए।
- 5दिखाइए कि Z का न्यूनतम मान दो बिंदुओं से अधिक बिंदुओं पर घटित होता है।View Solution
निम्न अवरोधों के अंतर्गत Z = 5x + 10y का न्यूनतमीकरण तथा अधिकतमीकरण कीजिए:
x + 2y $\leq$ 120, x + y $\geq$ 60, x - 2y $\geq$ 0, x $\geq$ 0 - 6ग्राफ़ीय विधि से निम्न रैखिक प्रोग्रामन समस्या को हल कीजिए:View Solution
निम्न अवरोधों के अंतर्गत Z = 5x + 3y का अधिकतमीकरण कीजिए:
3x + 5y $\leq$ 15, 5x + 2y $\leq$ 10, x $\geq$ 0, y $\geq$ 0 - 7View Solutionएक प्रकार के केक को 200 ग्राम आटा तथा 25 ग्राम वसा (fat) की आवश्यकता होती है तथा दूसरी प्रकार के केक के लिए 100 ग्राम आटा तथा 50 ग्राम वसा की आवश्यकता होती है। केकों की अधिकतम संख्या बताओ जो 5 किलो आटे तथा 1 किलो वसा से बन सकते हैं, यह मान लिया गया है कि केकों को बनाने के लिए अन्य पदार्थों की कमी नहीं रहेगी।
- 8आलेखीय विधि द्वारा उद्देश्य फलन Z = -50x + 20y का न्यूनतम मान निम्नलिखित व्यवरोधों के अंतर्गत ज्ञात कीजिए:View Solution
2x - y $\geq$ -5 ...(i)
3x + y $\geq$ 3 ...(ii)
2x - 3y $\leq$ 12 ...(iii)
x $\geq$ 0, y $\geq$ 0 ...(iv) - 9View Solutionएक कारखाने में दो प्रकार के पेंच A और B बनते हैं। प्रत्येक के निर्माण में दो मशीनों के प्रयोग की आवश्यकता होती है, जिसमें एक स्वचालित और दूसरी हस्तचालित है। एक पैकेट पेंच A के निर्माण में 4 मिनट स्वचालित और 6 मिनट हस्तचालित मशीन, तथा एक पैकेट पेंच B के निर्माण में 6 मिनट स्वचालित और 3 मिनट हस्तचालित मशीन का कार्य होता है। प्रत्येक मशीन किसी भी दिन के लिए अधिकतम 4 घंटे काम के लिए उपलब्ध है। निर्माता पेंच A के प्रत्येक पैकेट पर ₹7 और पेंच B के प्रत्येक पैकेट पर ₹10 का लाभ कमाता है। यह मानते हुए कि कारखाने में निर्मित सभी पेंचों के पैकेट बिक जाते हैं, ज्ञात कीजिए कि प्रतिदिन कितने पैकेट विभिन्न पेंचों के बनाए जाएँ जिससे लाभ अधिकतम हो तथा अधिकतम लाभ ज्ञात कीजिए।
- 10दिखाइए कि Z का न्यूनतम मान दो बिंदुओं से अधिक बिंदुओं पर घटित होता है।View Solution
निम्न अवरोधों के अंतर्गत Z = x + 2y का न्यूनतमीकरण तथा अधिकतमीकरण कीजिए:
x + 2y $\geq$ 100, 2x - y $\leq$ 0, 2x + y $\leq$ 200; x, y $\geq$ 0
