दर्शाइए कि बिंदु A(1, -2, -8), B(5, 0, -2) और C(11, 3, 7) संरेख है और B द्वारा AC को विभाजित करने वाला अनुपात ज्ञात कीजिए।
Miscellaneous Exercise-8
दिए गऐ बिंदु A(1, -2, -8), B(5, 0, -2) तथा C(11, 3, 7) है
$\vec{AB}$ = (B का स्थिति सदिश - A का स्थिति सदिश)
= $(5 \hat{{i}}+0 \hat{{j}}-2 \hat{{k}})$ - $(\hat{{i}}-2 \hat{{j}}-8 \hat{{k}})$
= (5 - 1)$ \hat{{i}}$ + (0+2)$ \hat{{j}}$ + (-2 + 8)$ \hat{{k}}$ = $4 \hat{{i}}+2 \hat{{j}}+6 \hat{{k}}$
|$\vec{AB}$| = $\sqrt{4^{2}+2^{2}+6^{2}}$ = $\sqrt{16+4+36}$ = $\sqrt{56}$ = $2 \sqrt{14}$
$\vec{BC}$ = (C का स्थिति सदिश - B का स्थिति सदिश)
= $(11 \hat{{i}}+3 \hat{{j}}+7 \hat{{k}})$ - $(5 \hat{{i}}+0 \hat{{j}}-2 \hat{{k}})$
= (11 - 5)$ \hat{{i}}$ + (3 - 0)$ \hat{{j}}$ + (7 + 2)$ \hat{{k}}$ = $6 \hat{{i}}+3 \hat{{j}}+9 \hat{{k}}$
|$\vec{BC}$| = $\sqrt{6^{2}+3^{2}+9^{2}}$ = $\sqrt{36+9+81}$ = $\sqrt{126}$ = $3 \sqrt{14}$
$\vec{AC}$ = (C का स्थिति सदिश - A का स्थिति सदिश)
= $(11 \hat{{i}}+3 \hat{{j}}+7 \hat{{k}})$ - $(\hat{{i}}-2 \hat{{j}}-8 \hat{{k}})$
= (11 - 1)$ \hat{{i}}$ + (3 + 2)$ \hat{{j}}$ + (7 + 8)$ \hat{{k}}$ = $10 \hat{{i}}+5 \hat{{j}}+15 \hat{{k}}$
|$\vec{AC}$| = $\sqrt{10^{2}+5^{2}+15^{2}}$ = $\sqrt{100+25+225}$ = $\sqrt{350}$ = $5 \sqrt{14}$
$\therefore$ |$\vec{AC}$| = |$\vec{AB}$| + |$\vec{BC}$|
अतः दिए गए बिंदु A, B तथा C संरेख हैं।
मान लीजिए रेखा AC पर बिंदु P इस प्रकार है कि वह |AC| को $\lambda$ : 1 के अनुपात में विभक्त करता हैं, तब
P का स्थिति सदिश =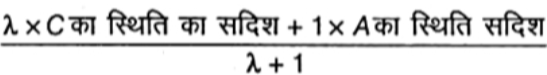
= $\frac{1}{\lambda+1}${$\lambda(11 \hat{{i}}+3 \hat{{j}}+7 \hat{{k}})$ + 1$(\hat{{i}}-2 \hat{{j}}-8 \hat{{k}})$}
= $\left(\frac{11 \lambda+1}{\lambda+1}\right) \hat{i}$ + $\left(\frac{3 \lambda-2}{\lambda+1}\right) \hat{j}$ + $\left(\frac{7 \lambda-8}{\lambda+1}\right) \hat{k}$
बिंदु B रेखा AC पर है अर्थात् बिंदु B, A तथा C संरेख हैं।
यदि P = B($\lambda$ के एक अद्वितीय मान के लिए)
$\Rightarrow$ $\left(\frac{11 \lambda+1}{\lambda+1}\right) \hat{{i}}$ + $\left(\frac{3 \lambda-2}{\lambda+1}\right) \hat{{j}}$ + $\left(\frac{7 \lambda-8}{\lambda+1}\right) \hat{{k}}$ = $5 \hat{{i}}+0 \hat{{j}}-2 \hat{{k}}$
$\Rightarrow$ $\frac{11 \lambda+1}{\lambda+1}$ = 5, $\frac{3 \lambda-2}{\lambda+1}$ = 0 तथा $\frac{7 \lambda-8}{\lambda+1}$ = -2
$\Rightarrow$ 11$ \lambda$ + 1 = 5$ \lambda$ + 5, 3$ \lambda$ = 2, 7$ \lambda$ -8 = -2$ \lambda$ -2
$\Rightarrow$ 6$ \lambda$ = 4, $ \lambda$ = $\frac23$, 9$ \lambda$ = 6 $\Rightarrow$ $ \lambda$ = $\frac23$
अतः A, B व C बिंदु संरेख हैं तथा बिंदु B, AC को $\frac{2}{3}$ : 1 के अनुपात में अर्थात् 2 : 3 के अनुपात में विभक्त करता है।
$\vec{AB}$ = (B का स्थिति सदिश - A का स्थिति सदिश)
= $(5 \hat{{i}}+0 \hat{{j}}-2 \hat{{k}})$ - $(\hat{{i}}-2 \hat{{j}}-8 \hat{{k}})$
= (5 - 1)$ \hat{{i}}$ + (0+2)$ \hat{{j}}$ + (-2 + 8)$ \hat{{k}}$ = $4 \hat{{i}}+2 \hat{{j}}+6 \hat{{k}}$
|$\vec{AB}$| = $\sqrt{4^{2}+2^{2}+6^{2}}$ = $\sqrt{16+4+36}$ = $\sqrt{56}$ = $2 \sqrt{14}$
$\vec{BC}$ = (C का स्थिति सदिश - B का स्थिति सदिश)
= $(11 \hat{{i}}+3 \hat{{j}}+7 \hat{{k}})$ - $(5 \hat{{i}}+0 \hat{{j}}-2 \hat{{k}})$
= (11 - 5)$ \hat{{i}}$ + (3 - 0)$ \hat{{j}}$ + (7 + 2)$ \hat{{k}}$ = $6 \hat{{i}}+3 \hat{{j}}+9 \hat{{k}}$
|$\vec{BC}$| = $\sqrt{6^{2}+3^{2}+9^{2}}$ = $\sqrt{36+9+81}$ = $\sqrt{126}$ = $3 \sqrt{14}$
$\vec{AC}$ = (C का स्थिति सदिश - A का स्थिति सदिश)
= $(11 \hat{{i}}+3 \hat{{j}}+7 \hat{{k}})$ - $(\hat{{i}}-2 \hat{{j}}-8 \hat{{k}})$
= (11 - 1)$ \hat{{i}}$ + (3 + 2)$ \hat{{j}}$ + (7 + 8)$ \hat{{k}}$ = $10 \hat{{i}}+5 \hat{{j}}+15 \hat{{k}}$
|$\vec{AC}$| = $\sqrt{10^{2}+5^{2}+15^{2}}$ = $\sqrt{100+25+225}$ = $\sqrt{350}$ = $5 \sqrt{14}$
$\therefore$ |$\vec{AC}$| = |$\vec{AB}$| + |$\vec{BC}$|
अतः दिए गए बिंदु A, B तथा C संरेख हैं।
मान लीजिए रेखा AC पर बिंदु P इस प्रकार है कि वह |AC| को $\lambda$ : 1 के अनुपात में विभक्त करता हैं, तब
P का स्थिति सदिश =
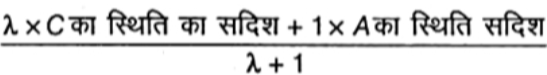
= $\frac{1}{\lambda+1}${$\lambda(11 \hat{{i}}+3 \hat{{j}}+7 \hat{{k}})$ + 1$(\hat{{i}}-2 \hat{{j}}-8 \hat{{k}})$}
= $\left(\frac{11 \lambda+1}{\lambda+1}\right) \hat{i}$ + $\left(\frac{3 \lambda-2}{\lambda+1}\right) \hat{j}$ + $\left(\frac{7 \lambda-8}{\lambda+1}\right) \hat{k}$
बिंदु B रेखा AC पर है अर्थात् बिंदु B, A तथा C संरेख हैं।
यदि P = B($\lambda$ के एक अद्वितीय मान के लिए)
$\Rightarrow$ $\left(\frac{11 \lambda+1}{\lambda+1}\right) \hat{{i}}$ + $\left(\frac{3 \lambda-2}{\lambda+1}\right) \hat{{j}}$ + $\left(\frac{7 \lambda-8}{\lambda+1}\right) \hat{{k}}$ = $5 \hat{{i}}+0 \hat{{j}}-2 \hat{{k}}$
$\Rightarrow$ $\frac{11 \lambda+1}{\lambda+1}$ = 5, $\frac{3 \lambda-2}{\lambda+1}$ = 0 तथा $\frac{7 \lambda-8}{\lambda+1}$ = -2
$\Rightarrow$ 11$ \lambda$ + 1 = 5$ \lambda$ + 5, 3$ \lambda$ = 2, 7$ \lambda$ -8 = -2$ \lambda$ -2
$\Rightarrow$ 6$ \lambda$ = 4, $ \lambda$ = $\frac23$, 9$ \lambda$ = 6 $\Rightarrow$ $ \lambda$ = $\frac23$
अतः A, B व C बिंदु संरेख हैं तथा बिंदु B, AC को $\frac{2}{3}$ : 1 के अनुपात में अर्थात् 2 : 3 के अनुपात में विभक्त करता है।
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1दो बिंदुओं P$(2 \vec{a}+\vec{b})$ और Q$(\vec{a}-3 \vec{b})$ को मिलाने वाली रेखा को 1 : 2 के अनुपात मे बाह्य विभाजित करने वाले बिंदु R का स्थिति सदिश ज्ञात कीजिए। यह भी दर्शाइए कि बिंदु P रेखाखंड RQ का मध्य बिंदु है।View Solution
- 2यदि एक मात्रक सदिश $\vec{a}, \hat{i}$ के साथ $\frac{\pi}{3}, \hat{j}$ के साथ $\frac{\pi}{4}$ और $\hat{k}$ साथ एक न्यून कोण $\theta$ बनाता है तो $\theta$ का मान ज्ञात कीजिए और इसकी सहायता से $\vec{a}$ के घटक भी ज्ञात कीजिए।View Solution
- 3यदि $\vec{a}, \vec{b}, \vec{c}$ मात्रक सदिश इस प्रकार है कि $\vec{a}+\vec{b}+\vec{c} = \overrightarrow{0}$ तो $\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c} + \vec{c} \cdot \vec{a}$ का मान ज्ञात कीजिए।View Solution
- 4मान लीजिए $\vec{a}$ = $\hat{i}+4 \hat{j}+2 \hat{k}$, $\vec{b}$ = $3 \hat{i}-2 \hat{j}+7 \hat{k}$ और $\vec{c}$ = $2 \hat{i}-\hat{j}+4 \hat{k}$ एक ऐसा सदिश $\vec{d}$ ज्ञात कीजिए जो $\vec{a}$ और $\vec{b}$ दोनों पर लंब है और $\vec{c} \cdot \vec{d}$ = 15.View Solution
- 5सदिश $\hat{i}+\hat{j}+\hat{k}$ का, सदिशों $2 \hat{i}+4 \hat{j}-5 \hat{k}$ और $\lambda \hat{i}+2 \hat{j}+3 \hat{k}$ के योगफल की दिशा में मात्रक सदिश के साथ अदिश गुणनफल $1$ के बराबर है तो $\lambda$ का मान ज्ञात कीजिए।View Solution
- 6मान लीजिए सदिश $\vec{a}, \vec{b}, \vec{c}$ क्रमश: $a_{1} \hat{i}+a_{2} \hat{j}+a_{3} \hat{k}$, $b_{1} \hat{i}+b_{2} \hat{j}+b_{3} \hat{k}$, $c_{1} \hat{i}+c_{2} \hat{j}+c_{3} \hat{k}$ के रूप में दिए हुए हैं तब दर्शाइए कि $\vec{a} \times(\vec{b}+\vec{c})$ = $\vec{a} \times \vec{b}$ + $\vec{a} \times \vec{c}$View Solution
- 7दर्शाइए कि दिए हुए निम्नलिखित तीन सदिशों में से प्रत्येक मात्रक सदिश है,View Solution
$\frac{1}{7}(2 \hat{i}+3 \hat{j}+6 \hat{k})$, $\frac{1}{7}(3 \hat{i}-6 \hat{j}+2 \hat{k})$, $\frac{1}{7}(6 \hat{i}+2 \hat{j}-3 \hat{k})$
यह भी दर्शाइए कि ये सदिश परस्पर एक दूसरे के लंबवत् हैं। - 8एक समांतर चतुर्भुज की संलग्न भुजाएँ $2 \hat{i}-4 \hat{j}+5 \hat{k}$ और $\hat{i}-2 \hat{j}-3 \hat{k}$ हैं। इसके विकर्ण के समांतर एक मात्रक सदिश ज्ञात कीजिए। इसका क्षेत्रफल भी ज्ञात कीजिए।View Solution
- 9दर्शाइए कि बिंदु $A, B$ और $C,$ जिनके स्थिति सदिश क्रमशः $\vec{a} = 3 \hat{i}-4 \hat{j}-4 \hat{k}, \vec{b} = 2 \hat{i}-\hat{j}+\hat{k}$ और $\vec{c} = \hat{i}-3 \hat{j}-5 \hat{k}$ हैं, एक समकोण त्रिभुज के शीर्षों का निर्माण करते हैं।View Solution
- 10View Solutionएक त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष A(1, 1, 2), B(2, 3, 5) और C(1, 5, 5) हैं।
