एक मीनार के पाद$-$बिंदु से एक भवन के शिखर का उन्नयन कोण $30^\circ$ है और भवन के पाद$-$बिंदु से मीनार के शिखर का उन्नयन कोण $60^\circ$ है। यदि मीनार $50 m$ ऊँची हो, तो भवन की ऊँचाई ज्ञात कीजिए।
Exercise-9.1-9
आकृति में,
माना भवन की ऊँचाई $= AB = h$ मी.
और मीनार की ऊँचाई $= CD = 50 $ मी.
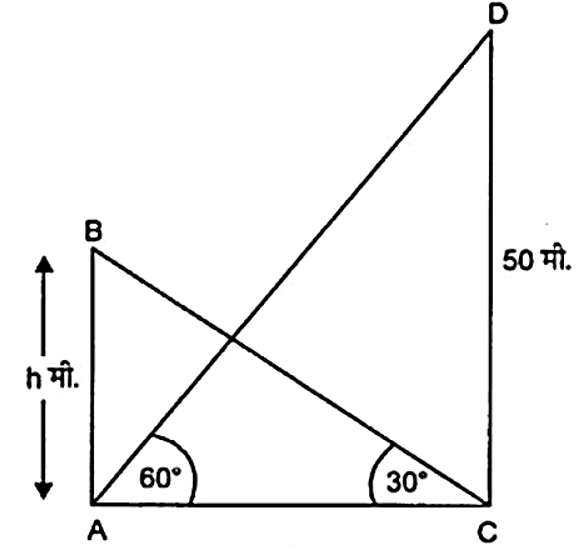
अब, समकोण $\triangle ABC$ में
$\frac{AC}{AB} = \cot 30^\circ = \sqrt{3}$
$\Rightarrow \frac{\mathrm{AC}}{h}=\sqrt{3}$
$ \Rightarrow AC = h \sqrt{3} ...(i)$
पुन: समकोण $\triangle DCA$ में,
$\frac{\mathrm{DC}}{\mathrm{AC}} = \tan 60^\circ$
$\Rightarrow \frac{50}{\mathrm{AC}}=\sqrt{3} $
$\Rightarrow \mathrm{AC}=\frac{50}{\sqrt{3}} ...(ii)$
$(i)$ और $(ii)$ से,
$\sqrt{3} h=\frac{50}{\sqrt{3}}$
$\Rightarrow h = \frac{50}{\sqrt{3}} \times \frac{1}{\sqrt{3}}=\frac{50}{3}=16 \frac{2}{3}$
इस प्रकार, भवन की ऊँचाई $= 16\frac{2}{3}$ मी.
माना भवन की ऊँचाई $= AB = h$ मी.
और मीनार की ऊँचाई $= CD = 50 $ मी.

अब, समकोण $\triangle ABC$ में
$\frac{AC}{AB} = \cot 30^\circ = \sqrt{3}$
$\Rightarrow \frac{\mathrm{AC}}{h}=\sqrt{3}$
$ \Rightarrow AC = h \sqrt{3} ...(i)$
पुन: समकोण $\triangle DCA$ में,
$\frac{\mathrm{DC}}{\mathrm{AC}} = \tan 60^\circ$
$\Rightarrow \frac{50}{\mathrm{AC}}=\sqrt{3} $
$\Rightarrow \mathrm{AC}=\frac{50}{\sqrt{3}} ...(ii)$
$(i)$ और $(ii)$ से,
$\sqrt{3} h=\frac{50}{\sqrt{3}}$
$\Rightarrow h = \frac{50}{\sqrt{3}} \times \frac{1}{\sqrt{3}}=\frac{50}{3}=16 \frac{2}{3}$
इस प्रकार, भवन की ऊँचाई $= 16\frac{2}{3}$ मी.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1भूमि के एक बिंदु से एक $20 m$ ऊँचे भवन के शिखर पर लगी एक संचार मीनार के तल और शिखर के उन्नयन कोण क्रमशः $45^\circ$ और $60^\circ$ है। मीनार की ऊँचाई ज्ञात कीजिए।View Solution
- 2$1.5 m$ लंबा एक लड़का $30 m$ ऊँचे एक भवन से कुछ दूरी पर खड़ा है। जब वह ऊँचे भवन की ओर जाता है तब उसकी आँख से भवन के शिखर का उन्नयन कोण $30^\circ$ से $60^\circ$ हो जाता है। बताइए कि वह भवन की ओर कितनी दूरी तक चलकर गया है।View Solution
- 3एक सीधा राजमार्ग एक मीनार के पाद तक जाता है। मीनार के शिखर पर खड़ा एक आदमी एक कार को $30^\circ$ के अवनमन कोण पर देखता है जो कि मीनार के पाद की ओर एक समान चाल से जाता है। छ: सेकेंड बाद कार का अवनमन कोण $60^\circ$ हो गया। इस बिंदु से मीनार के पाद तक पहुँचने में कार द्वारा लिया गया समय ज्ञात कीजिए।View Solution
- 4आँधी आने से एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है कि पेड़ का शिखर जमीन को छूने लगता है और इसके साथ $30^\circ$ का कोण बनाता है। पेड़ के पाद$-$बिंदु की दूरी, जहाँ पेड़ का शिखर जमीन को छूता है$, 8 m$ है। पेड़ की ऊँचाई ज्ञात कीजिए।View Solution
- 5$7 m$ ऊँचे भवन के शिखर से एक केबल टॉवर के शिखर का उन्नयन कोण $60^\circ$ है और इसके पाद का अवनमन कोण $45^\circ$ है। टॉवर की ऊँचाई ज्ञात कीजिए।View Solution
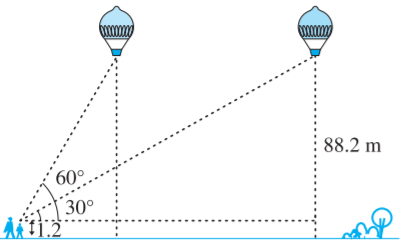
- 6$1.2 m$ लंबी एक लड़की भूमि से $88.2 m$ की ऊँचाई पर एक क्षैतिज रेखा में हवा में उड़ रहे गुब्बारे को देखती है। किसी भी क्षण लड़की की आँख से गुब्बारे का उन्नयन कोण $60^\circ$ है। कुछ समय बाद उन्नयन कोण घटकर $30^\circ$ हो जाता है $($देखिए आकृति$)।$ इस अंतराल के दौरान गुब्बारे द्वारा तय की गई दूरी ज्ञात कीजिए।View Solution
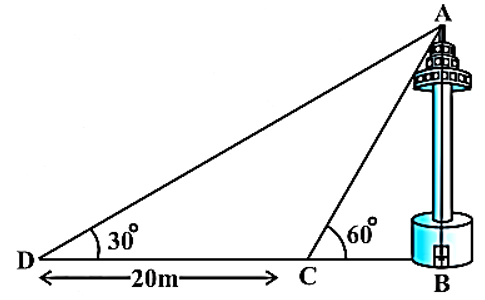
- 7एक नहर के एक तट पर एक टीवी टॉवर ऊर्ध्वाधरतः खड़ा है। टॉवर के ठीक सामने दूसरे तट के एक अन्य बिंदु से टॉवर के शिखर का उन्नयन कोण $60^\circ$ है। इसी तट पर इस बिंदु से $20 m$ दूर और इस बिंदु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिंदु से टॉवर के शिखर का उन्नयन कोण $30^\circ$ है। $($देखिए आकृति$)$। टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए।View Solution
- 8भूमि के एक बिंदु से, जो मीनार के पाद$-$बिंदु से $30 m$ की दूरी पर है, मीनार के शिखर का उन्नयन कोण $30^\circ$ है। मीनार की ऊँचाई ज्ञात कीजिए।View Solution
- 9एक ठेकेदार बच्चों को खेलने के लिए एक पार्क में दो फिसलनपट्टी लगाना चाहती है। $5$ वर्ष से कम उम्र के बच्चों के लिए वह एक ऐसी फिसलनप्टी लगाना चाहती है जिसका शिखर $1.5 m$ की ऊँचाई पर हो और भूमि के साथ $30^\circ$ के कोण पर झुका हुआ हो, जबकि इससे अधिक उम्र के बच्चों के लिए वह $3 m$ की ऊँचाई पर एक अधिक ढाल की फिसलनपट्टी लगाना चाहती है, जो भूमि के साथ $60^\circ$ का कोण बनाती हो। प्रत्येक स्थिति में फिसलनपट्टी की लंबाई क्या होनी चाहिए?View Solution
- 10मीनार के आधार से और एक सरल रेखा में $4 m$ और $9 m$ की दूरी पर स्थित दो बिंदुओं से मीनार के शिखर के उन्नयन कोण पूरक कोण हैं। सिद्ध कीजिए कि मीनार की ऊँचाई $6 m$ है।View Solution
