एक सिक्के को उछालने के परीक्षण पर विचार कीजिए। यदि सिक्के पर चित प्रकट हो तो सिक्के को पुनः उछालें परंतु यदि सिक्के पर पट प्रकट हो तो एक पासे को फेंकें। यदि घटना कम से कम एक पट प्रकट होना का घटित होना दिया गया है तो घटना पासे पर 4 से बड़ी संख्या प्रकट होना की सप्रतिबंध प्रायिकता ज्ञात कीजिए।
example-7
परीक्षण के परिणामों को चित्र से व्यक्त किया जा सकता है। इस प्रकार के चित्र को वृक्षारेख कहते हैं।
पट (T) परीक्षण का प्रतिदर्श समष्टि है:
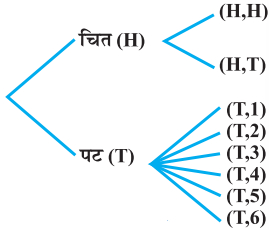
S = {(H, H), (H, T), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (T, 6)}
जहाँ (H, H) दर्शाता है कि दोनों उछालों पर चित प्रकट हुआ है, तथा (T, i) दर्शाता है कि पहली उछाल पर पट प्रकट हुआ और पासे को फेंकने पर संख्या i प्रकट हुई।
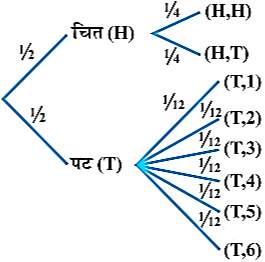
अतः 8 मौलिक घटनाओं (H, H), (H, T), (T, 1), (T, 2), (T, 3)(T, 4), (T, 5), (T, 6)की क्रमशः $: \frac{1}{4}, \frac{1}{4}, \frac{1}{12}, \frac{1}{12}, \frac{1}{12}, \frac{1}{12}, \frac{1}{12}, \frac{1}{12}$ प्रायिकता निर्धारित की जा सकती है, जैसा कि चित्र से स्पष्ट है।
मान लें F घटना 'न्यूनतम एक पट प्रकट होना' और E से पर 4 से बड़ी संख्या प्रकट होना' को दर्शाते हैं।
तब F = {(H, T), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (T, 6)}
$\mathrm{E} $ = $\{(\mathrm{T}, 5), \mathrm{T}, 6)\} $और $\mathrm{E} \cap \mathrm{F}$$=\{(\mathrm{T}, 5),(\mathrm{T}, 6)\} $
अब $\mathrm{P}(\mathrm{F})$ = P({(H, T)}) + P({(T, 1)}) + P({(T, 2)}) + P({(T, 3)}) + P({(T, 4)}) + P({(T, 5)}) + P({(T, 6)})
= $\frac{1}{4}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}=\frac{3}{4} $
और $\mathrm{P}(\mathrm{E} \cap \mathrm{F}) =\mathrm{P}(\{(\mathrm{T}, 5)\})+\mathrm{P}(\{(\mathrm{T}, 6)\})$ = $\frac{1}{12}+\frac{1}{12}=\frac{1}{6}$
अतः $P(E \mid F)=\frac{P(E \cap F)}{P(F)}=\frac{\overline{6}}{\frac{3}{4}}=\frac{2}{9} $
पट (T) परीक्षण का प्रतिदर्श समष्टि है:

S = {(H, H), (H, T), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (T, 6)}
जहाँ (H, H) दर्शाता है कि दोनों उछालों पर चित प्रकट हुआ है, तथा (T, i) दर्शाता है कि पहली उछाल पर पट प्रकट हुआ और पासे को फेंकने पर संख्या i प्रकट हुई।

अतः 8 मौलिक घटनाओं (H, H), (H, T), (T, 1), (T, 2), (T, 3)(T, 4), (T, 5), (T, 6)की क्रमशः $: \frac{1}{4}, \frac{1}{4}, \frac{1}{12}, \frac{1}{12}, \frac{1}{12}, \frac{1}{12}, \frac{1}{12}, \frac{1}{12}$ प्रायिकता निर्धारित की जा सकती है, जैसा कि चित्र से स्पष्ट है।
मान लें F घटना 'न्यूनतम एक पट प्रकट होना' और E से पर 4 से बड़ी संख्या प्रकट होना' को दर्शाते हैं।
तब F = {(H, T), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (T, 6)}
$\mathrm{E} $ = $\{(\mathrm{T}, 5), \mathrm{T}, 6)\} $और $\mathrm{E} \cap \mathrm{F}$$=\{(\mathrm{T}, 5),(\mathrm{T}, 6)\} $
अब $\mathrm{P}(\mathrm{F})$ = P({(H, T)}) + P({(T, 1)}) + P({(T, 2)}) + P({(T, 3)}) + P({(T, 4)}) + P({(T, 5)}) + P({(T, 6)})
= $\frac{1}{4}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}=\frac{3}{4} $
और $\mathrm{P}(\mathrm{E} \cap \mathrm{F}) =\mathrm{P}(\{(\mathrm{T}, 5)\})+\mathrm{P}(\{(\mathrm{T}, 6)\})$ = $\frac{1}{12}+\frac{1}{12}=\frac{1}{6}$
अतः $P(E \mid F)=\frac{P(E \cap F)}{P(F)}=\frac{\overline{6}}{\frac{3}{4}}=\frac{2}{9} $
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionदो गेंद एक बॉक्स से बिना प्रतिस्थापित किए निकाली जाती है। बॉक्स में 10 काली और 8 लाल गेदें हैं, तो प्रायिकता ज्ञात कीजिए।
- दोनों गेंदे लाल हों
- प्रथम काली एवं दूसरी लाल हो
- एक काली तथा दूसरी लाल हो।
- 2View Solutionताश के 52 पत्तों की एक भली-भाँति फेंटी गई गड्डी में से दो पत्ते उत्तरोत्तर बिना प्रतिस्थापना के (या एक साथ) निकाले जाते हैं। बादशाहों की संख्या का माध्य, प्रसरण व मानक-विचलन ज्ञात कीजिए।
- 3तीन अभिन्न डिब्बे $I, II$ और $III$ दिए गए हैं जहाँ प्रत्येक में दो सिक्के हैं। डिब्बे $I$ में दोनों सिक्के सोने के है, डिब्बे $II$ में दोनों सिक्के चाँदी के हैं और डिब्बे $III$ में एक सोने और एक चाँदी का सिक्का है। एक व्यक्ति यादृच्छया एक डिब्बा चुनता है और उसमें से यादृच्छया एक सिक्का निकालता है। यदि सिक्का सोने का है, तो इस बात की क्या प्रायिकता है कि डिब्बे में दूसरा सिक्का भी सोने का ही है$?$View Solution
- 4द्विपद बंटन $B \left(4, \frac{1}{3}\right)$ का माध्य ज्ञात कीजिए।View Solution
- 5View Solutionपासों के एक जोड़े को तीन बार उछालने पर द्विकों (doublets) की संख्या का प्रायिकता बंटन ज्ञात कीजिए।
- 6एक सिक्के को तीन बार उछाला गया हैView Solution
- $E :$ तीसरी उछाल पर चित $F :$ पहली दोनों उछालों पर चित
- $E :$ न्यूनतम दो चित $F :$ अधिकतम एक चित
- $E :$ अधिकतम दो पट$ F :$ न्यूनतम दो पट
- 7एक बीमा कंपनी $2000$ स्कूटर चालकों, $4000$ कार चालकों और $6000$ ट्रक चालकों का बीमा करती है। दुर्घटनाओं की प्रायिकताएँ क्रमशः $0.01, 0.03$ और $0.15$ है। बीमाकृत व्यक्तियों $($चालकों$)$ में से एक दुर्घटनाग्रस्त हो जाता है। उस व्यक्ति के स्कूटर चालक होने की प्रायिकता क्या है?View Solution
- 8दो दल एक निगम के निर्देशक मंडल में स्थान पाने की प्रतिस्पर्धा में हैं। पहले तथा दूसरे दल के जीतने की प्रायिकताएँ क्रमशः $0.6$ तथा $0.4$ हैं। इसके अतिरिक्त यदि पहला दल जीतता है तो एक नए उत्पाद के प्रारम्भ होने की प्रायिकता $0.7$ है और यदि दूसरा दल जीतता है, तो इस बात की संगत प्रायिकता $0.3$ है। इसकी प्रायिकता ज्ञात कीजिए कि नया उत्पादन दूसरे दल द्वारा प्रारम्भ किया गया था।View Solution
- 9एक न्याय्य पासे को उछाला गया है। घटनाओं E = {1, 3, 5}, F = {2, 3} और G = {2, 3, 4, 5} के लिए निम्नलिखित को ज्ञात कीजिए।View Solution
- P$\left(\frac{E}{F}\right)$ तथा $P\left(\frac{F}{E}\right)$
- P$\left(\frac{E}{G}\right)$ तथा P$\left(\frac{G}{E}\right)$
- P$\left(\frac{E \cup F}{G}\right)$तथा P$\left(\frac{E \cap F}{G}\right)$
- 10एक कक्षा में $15$ छात्र हैं जिनकी आयु $14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19$ और $20$ वर्ष हैं। एक छात्र को इस प्रकार चुना गया कि प्रत्येक छात्र को चुने जाने की संभावना समान है और चुने गए छात्र की आयु $(X)$ को लिखा गया। यादुच्छिक चर $X$ का प्रायिकता बंटन ज्ञात कीजिए। $X$ का माध्य, प्रसरण व मानक विचलन भी ज्ञात कीजिए।View Solution
