एक वृत्ताकार तालाब का व्यास $17.5 m$ है। इसके अनुदिश बाहर की ओर $2 m$ चौड़ा एक पथ बना हुआ है। $25$ रु प्रति वर्ग मीटर की दर से इस पथ के निर्माण की लागत ज्ञात कीजिए।
Exercise-11.4-5
Download our app for free and get started
एक तालाब की त्रिज्या $=\frac{17.5}{2} = 8.75$
एक तालाब का क्षेत्रफल $= \pi(8.75)^2$ वर्ग मीटर
पथ सहित वृत्त की त्रिज्या $= 8.75 + 2 = 10.75 m$
प्रश्न के अनुसार,
पथ का क्षेत्रफल $=$ पथ सहित वृत्त का क्षेत्रफल $-$ तालाब का क्षेत्रफल
$= \pi(10.75)^2 - \pi(8.75)^2$
$= \pi[(10.75)^2 - (8.75)^2]$
$=\frac{22}{7} \times 39$
$=\frac{858}{7}$ वर्ग मीटर
$= 122.46$ वर्गमीटर
पथ के निर्माण की लागत $= 25 \times 122.46 = ₹ 3061.50$
एक तालाब का क्षेत्रफल $= \pi(8.75)^2$ वर्ग मीटर
पथ सहित वृत्त की त्रिज्या $= 8.75 + 2 = 10.75 m$
प्रश्न के अनुसार,
पथ का क्षेत्रफल $=$ पथ सहित वृत्त का क्षेत्रफल $-$ तालाब का क्षेत्रफल
$= \pi(10.75)^2 - \pi(8.75)^2$
$= \pi[(10.75)^2 - (8.75)^2]$
$=\frac{22}{7} \times 39$
$=\frac{858}{7}$ वर्ग मीटर
$= 122.46$ वर्गमीटर
पथ के निर्माण की लागत $= 25 \times 122.46 = ₹ 3061.50$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1व्यास $20 \ cm$ वाले वृत्त की एक जीवा उसके केंद्र पर $90^\circ$ का कोण बनाती है। इस वृत्त के संगत दीर्घ वृत्तखंड का क्षेत्रफल ज्ञात कीजिए $(\pi = 3.14$ का प्रयोग कीजिए$)।$View Solution
- 2बराबर त्रिज्या $3.5 \ cm$ वाले तीन वृत्त इस प्रकार खींचे गये हैं कि इनमें से प्रत्येक अन्य दो वृत्तों को स्पर्श करता है। इन वृत्तों से परिबद्ध क्षेत्रफल ज्ञात कीजिए।View Solution
- 3त्रिज्या $5 \ cm$ वाले वृत्त के उस त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए जिसके संगत चाप की लंबाई $3.5 \ cm$ है।View Solution
- 4बराबर त्रिज्या $7 \ cm$ त्रिज्या वाले चार वृत्ताकार गत्ते के टुकड़ों को एक कागज पर इस प्रकार रखा गया है कि प्रत्येक टुकड़ा अन्य दो टुकड़ों को स्पर्श करता है। इन टुकड़ों के बीच में परिबद्ध भाग का क्षेत्रफल ज्ञात कीजिए।View Solution
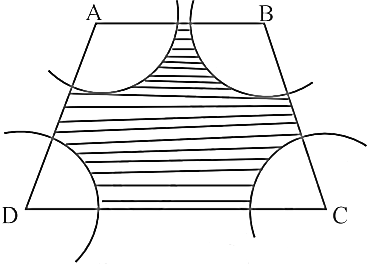
- 5आकृति में, $\text{ABCD}$ एक समलंब है, जिसमें $AB \| DC, AB = 18 \ cm, DC = 32 \ cm$ तथा $AB$ और $DC$ के बीच की दूरी $= 14 \ cm$ है। यदि $\text{A, B, C}$ और $D$ को केंद्र मानकर त्रिज्याओं $7 \ cm$ के चाप खींचे गये हैं, तो इस आकृति के छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।View Solution
- 6त्रिज्या $21 \ cm$ वाले एक वृत्त के $120^\circ$ कोण वाले त्रिज्यखंड और उसके संगत दीर्घ त्रिज्यखंड के क्षेत्रफलों का अंतर ज्ञात कीजिए।View Solution
- 7वृत्त की उस जीवा द्वारा निर्मित दोनों वृत्तखंडों के क्षेत्रफलों का अंतर ज्ञात कीजिए, जिसकी लंबाई $5 \ cm$ है और जो केंद्र पर $90^\circ$ का कोण अंतरित करती है।View Solution
- 8त्रिज्या $12 \ cm$ वाले वृत्त के उस वृत्तखंड का क्षेत्रफल ज्ञात कीजिए, जिसके संगत त्रिज्यखंड का केंद्रीय कोण $60^\circ$ है।View Solution
- 9$176 m$ की दूरी तय करने $($घूमने$)$ में, $1.54 m^2$ क्षेत्रफल वाले एक वृत्ताकार पहिये द्वारा लगाये जाने वाले चक्करों की संख्या ज्ञात कीजिए।View Solution
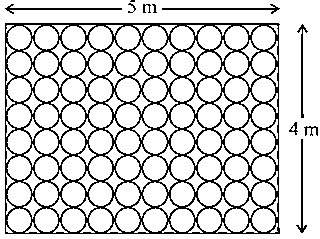
- 10किसी कमरे के फर्श की विमाएँ $5 m \times 4 m$ हैं और इस पर वृत्ताकार टाइलें लगायी जाती हैं, जिनमें से प्रत्येक का व्यास $50 \ cm$ है, जैसा कि आकृति में दर्शाया गया है। फर्श के उस भाग का क्षेत्रफल ज्ञात कीजिए जिस पर टाइल नहीं लगी हैं $(\pi = 3.14$ का प्रयोग कीजिए$)$।View Solution
