निम्न अवरोधों के अंतर्गत Z = 3x + 5y का न्यूनतमीकरण कीजिए:
x + 3y $\geq$ 3, x + y $\geq$ 2, x, y $\geq$ 0
Z = 3x + 5y ...(i)
का निम्नतम मान निम्न व्यवरोधों के अंतर्गत ज्ञात करना है।
x + 3y $\geq$ 3 ...(ii)
x + y $\geq$ 2 ...(iii)
x, y $\geq$ 0 ...(iv)
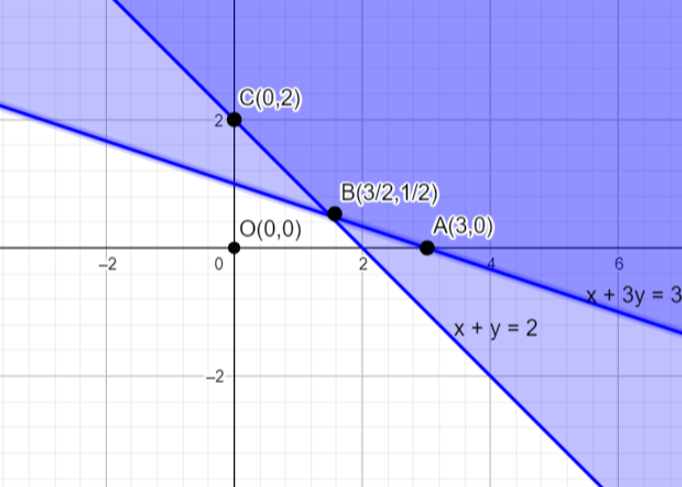
सर्वप्रथम, रेखा x + 3y = 3 का ग्राफ खींचते हैं।
| x | 0 | 3 |
| y | 1 | 0 |
(0, 0) असमिका x + 3y $\geq$ 0, में रखने पर,
0 + 3 $\times$ 0 $\geq$ 3 $\Rightarrow$ 0 $\geq$ 3 (जोकि असत्य है)
अतः अर्द्धतल मूलबिंदु के विपरीत ओर है। चूँकि बिंदु x, y $\geq$ 0, अतः सुसंगत क्षेत्र प्रथम चतुर्थांश में स्थित होगा।
अब, रेखा x + y = 2 का ग्राफ खींचते हैं।
| x | 0 | 2 |
| y | 2 | 0 |
(0, 0) असमिका x + y $\geq$ 2, में रखने पर,
0 + 0 $\geq$ 2 $\Rightarrow$ 0 $\geq$ 2 (जोकि असत्य है)
अतः अर्द्धतल मूलबिंदु के विपरीत ओर है। स्पष्ट है कि सुसंगत क्षेत्र अपरिबद्ध है।
समीकरण x + y = 2 तथा x + 3y = 3 को हल करने पर, x = $\frac{3}{2}$ तथा y = $\frac{1}{2}$ प्राप्त होता है।
$\therefore$ प्रतिच्छेद बिंदु B$\left(\frac{3}{2}, \frac{1}{2}\right)$ है।
इस प्रकार, सुसंगत क्षेत्र के शीर्ष बिंदु O(0, 0), A(3, 0), B$\left(\frac{3}{2}, \frac{1}{2}\right)$ तथा C(0, 2) हैं। इन शीर्ष बिंदुओं पर Z का मान निम्न है।
| शीर्ष बिंदु | Z = 3x + 5y |
| O(0, 0) | 0 |
| A(3, 0) | 9 |
| B$\left(\frac{3}{2}, \frac{1}{2}\right)$ | 7 $\rightarrow$ निम्नतम |
| C(0, 2) | 10 |
चूँकि सुसंगत क्षेत्र अपरिबंद्ध है। अतः Z का निम्नतम मान 7 हो भी सकता है और नहीं भी हो सकता है। असमिका 3x + 5y < 7 का ग्राफ खींचकर देखते हैं कि प्राप्त अर्द्धतल तथा सुसंगत क्षेत्र में उभयनिष्ठ बिंदु है या नहीं।
अतः सुसंगत क्षेत्र में 3x + 5y < 7 के अर्द्धतल में कोई उभयनिष्ठ बिंदु नहीं है।
अतः Z का निम्नतम मान 7 है जोकि बिंदु $\left(\frac{3}{2}, \frac{1}{2}\right)$ पर प्राप्त होता है।
Download our appand get started for free
Similar Questions
- 1View Solutionरेशमा दो प्रकार के भोज्य P और Q को इस प्रकार मिलाना चाहती है कि मिश्रण में विटामिन अवयवों में 8 मात्रक विटामिन A तथा 11 मात्रक विटामिन B हों। भोज्य P की लागत ₹60/kg और भोज्य Q की लागत ₹80/kg है। भोज्य P में 3 मात्रक/kg विटामिन A और 5 मात्रक/kg विटामिन B है जबकि भोज्य Q में 4 मात्रक/kg विटामिन A और 2 मात्रक/kg विटामिन है। मिश्रण की न्यूनतम लागत ज्ञात कीजिए।
- 2View Solutionएक प्रकार के केक को 200 ग्राम आटा तथा 25 ग्राम वसा (fat) की आवश्यकता होती है तथा दूसरी प्रकार के केक के लिए 100 ग्राम आटा तथा 50 ग्राम वसा की आवश्यकता होती है। केकों की अधिकतम संख्या बताओ जो 5 किलो आटे तथा 1 किलो वसा से बन सकते हैं, यह मान लिया गया है कि केकों को बनाने के लिए अन्य पदार्थों की कमी नहीं रहेगी।
- 3दिखाइए कि Z का न्यूनतम मान दो बिंदुओं से अधिक बिंदुओं पर घटित होता है।View Solution
निम्न अवरोधों के अंतर्गत Z = x + 2y का न्यूनतमीकरण तथा अधिकतमीकरण कीजिए:
x + 2y $\geq$ 100, 2x - y $\leq$ 0, 2x + y $\leq$ 200; x, y $\geq$ 0 - 4दिखाइए कि Z का न्यूनतम मान दो बिंदुओं से अधिक बिंदुओं पर घटित होता है।View Solution
निम्न अवरोधों के अंतर्गत Z = 5x + 10y का न्यूनतमीकरण तथा अधिकतमीकरण कीजिए:
x + 2y $\leq$ 120, x + y $\geq$ 60, x - 2y $\geq$ 0, x $\geq$ 0 - 5एक भोज्य पदार्थ में कम से कम $80$ मात्रक विटामिन $A$ और $100$ मात्रक खनिज होना चाहिए। दो प्रकार के भोज्य $F_1$ और $F_2$ उपलब्ध हैं। भोज्य $F_1$ की लागत $₹\ 4$प्रति मात्रक और $F_2$ की लागत $₹\ 5$ प्रति मात्रक है। भोज्य $F_1$ की एक इकाई में कम से कम $3$ मात्रक विटामिन $A$ और $4$ मात्रक खनिज है। $F_2$ की प्रति इकाई में कम से कम $6$ मात्रक विटामिन $A$ और $3$ मात्रक खनिज हैं। इसको एक रैखिक प्रोग्रामन समस्या के रूप में सूत्रबद्ध कीजिए। उस आहार का न्यूनतम मूल्य ज्ञात कीजिए, जिसमें इन दो भोज्यों का मिश्रण है और उसमें न्यूनतम पोषक तत्व हैं।View Solution
- 6ग्राफ़ीय विधि से रैखिक प्रोग्रामन समस्या को हल कीजिए:View Solution
निम्न अवरोधों के अंतर्गत Z = 3x + 2y का न्यूनतमीकरण कीजिए:
x + 2y $\leq$ 10, 3x + y $\leq$ 15, x, y $\geq$ 0 - 7दो प्रकार के उर्वरक $F_1$ और $F_2$ है। $F_1$ में $10\%$ नाइट्रोजन और $6\%$ फास्फोरिक अम्ल है। तथा $F_2$ में $5\%$ नाइट्रोजन तथा $10\%$ फास्फोरिक अम्ल है। मिट्टी की स्थितिओं का परीक्षण करने के पश्चात् एक किसान पाता है कि उसे अपनी फसल के लिए $14 \ kg$ नाइट्रोजन और $14 \ kg$ फास्फोरिक अम्ल की आवश्यकता है। यदि $F_1$ की कीमत $₹\ 6/ kg$ और $F_2$ की कीमत $₹\ 5/ kg$ है, प्रत्येक प्रकार का कितना उर्वरक उपयोग के लिए चाहिए ताकि न्यूनतम मूल्य पर वांछित पोषक तत्व मिल सके। न्यूनतम लागत क्या है।View Solution
- 8View Solutionएक निर्माता दो प्रकार के खिलौने A और B बनाता है। इस उद्देश्य के लिए निर्माण में तीन मशीनों की आवश्यकता पड़ती है और प्रत्येक प्रकार के खिलौने के निर्माण के लिए लगा समय (मिनटों में) निम्नलिखित है।
खिलौने के प्रकार मशीन I II III A 12 18 6 B 6 0 9 प्रत्येक मशीन अधिकतम 6 घंटे प्रतिदिन के लिए उपलब्ध है। यदि A प्रकार के खिलौने की बिक्री पर ₹7.50 लाभ और B प्रकार के खिलौने पर ₹5 का लाभ हो तो दर्शाइए कि अधिकतम लाभ कमाने के लिए प्रतिदिन A प्रकार के 15 खिलौने और B प्रकार 30 खिलौने निर्मित होने चाहिए।
- 9आलेखीय विधि द्वारा उद्देश्य फलन Z = -50x + 20y का न्यूनतम मान निम्नलिखित व्यवरोधों के अंतर्गत ज्ञात कीजिए:View Solution
2x - y $\geq$ -5 ...(i)
3x + y $\geq$ 3 ...(ii)
2x - 3y $\leq$ 12 ...(iii)
x $\geq$ 0, y $\geq$ 0 ...(iv) - 10View Solutionएक कारखाने में दो प्रकार के पेंच A और B बनते हैं। प्रत्येक के निर्माण में दो मशीनों के प्रयोग की आवश्यकता होती है, जिसमें एक स्वचालित और दूसरी हस्तचालित है। एक पैकेट पेंच A के निर्माण में 4 मिनट स्वचालित और 6 मिनट हस्तचालित मशीन, तथा एक पैकेट पेंच B के निर्माण में 6 मिनट स्वचालित और 3 मिनट हस्तचालित मशीन का कार्य होता है। प्रत्येक मशीन किसी भी दिन के लिए अधिकतम 4 घंटे काम के लिए उपलब्ध है। निर्माता पेंच A के प्रत्येक पैकेट पर ₹7 और पेंच B के प्रत्येक पैकेट पर ₹10 का लाभ कमाता है। यह मानते हुए कि कारखाने में निर्मित सभी पेंचों के पैकेट बिक जाते हैं, ज्ञात कीजिए कि प्रतिदिन कितने पैकेट विभिन्न पेंचों के बनाए जाएँ जिससे लाभ अधिकतम हो तथा अधिकतम लाभ ज्ञात कीजिए।
