किसी मोहल्ले के एक शॉपिंग कांप्लेक्स (shopping complex) की 30 दुकानों द्वारा अर्जित किए गए वार्षिक लाभों से निम्नलिखित बारंबारता बंटन प्राप्त होता है:
| लाभ (लाख रुपयों में) | दुकानों की संख्या |
| 5 से अधिक या उसके बराबर | 30 |
| 10 से अधिक या उसके बराबर | 28 |
| 15 से अधिक या उसके बराबर | 16 |
| 20 से अधिक या उसके बराबर | 14 |
| 25 से अधिक या उसके बराबर | 10 |
| 30 से अधिक या उसके बराबर | 7 |
| 35 से अधिक या उसके बराबर | 3 |
उपरोक्त आँकड़ों के लिए एक ही अक्षों पर दोनों तोरण खींचिए। इसके बाद, माध्यक लाभ ज्ञात कीजिए।
example-9
Download our app for free and get started
पहले हम ग्राफ पेपर पर क्षैतिज और ऊर्ध्वाधर अक्ष खींचते हैं, जिनमें लाभ के अंतरालों की निम्न सीमाएँ क्षैतिज अक्ष के अनुदिश लेते हैं और संचयी बारंबारताओं का ऊर्ध्वाधर अक्ष के अनुदिश लेते हैं। फिर हम बिंदुओं (5, 30), (10, 28), (15, 16), (20, 14), (25, 10), (30, 7) और (35, 3) को आलेखित करके एक मुक्त हस्त वक्र से मिला देते हैं। इससे हमें 'से अधिक के प्रकार का' तोरण प्राप्त हो जाता है, जैसाकि आकृति में दर्शाया गया है।
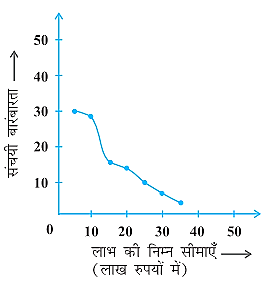
अब आइए उपरोक्त सारणी से, वर्ग अंतराल, संगत बारबारताएँ और संचयी बारबारताएँ प्राप्त करें|
सारणी
| वर्ग अंतराल | 5 - 10 | 10 - 15 | 15 - 20 | 20 - 25 | 25 - 30 | 30 - 35 | 35 - 40 |
| दुकानों की संख्या | 2 | 12 | 2 | 4 | 3 | 4 | 3 |
| संचयी बारंबारता | 2 | 14 | 16 | 20 | 23 | 27 | 30 |
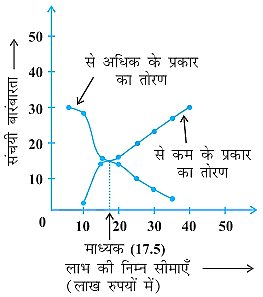
इन मानों का प्रयोग करके हम (10, 2), (15, 14), (20, 16), (25, 20), (30, 23), (35, 27), (40, 30) को आकृति वाले आलेख में आलेखित करते हैं। फिर इनको एक मुक्त हस्त वक्र द्वारा मिलाकर 'से कम के प्रकार का' तोरण प्राप्त करते हैं, जैसाकि आकृति में दर्शाया गया है। इनके प्रतिच्छेद बिंदु से क्षैतिज अक्ष पर लंब डालने पर जो क्षैतिज अक्ष और लंब का प्रतिच्छेद बिंदु है, उसी के संगत मान से माध्यक प्राप्त होता है। यह माध्यक 17.5 लाख रुपये है।
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1निम्नलिखित सारणी किसी अस्पताल में एक विशेष वर्ष में भर्ती हुए रोगियों की आयु को दर्शाती है:View Solution
उपरोक्त आँकड़ों के बहुलक और माध्य ज्ञात कीजिए। दोनों केंद्रीय प्रवृत्ति की मापों की तुलना कीजिए और उनकी व्याख्या कीजिए।आयु $($वर्षों में$)$ $5-15$ $15-25$ $25-35$ $35-45$ $45-55$ $55-65$ रोगियों की संख्या $6$ $11$ $21$ $23$ $14$ $5$ - 2निम्नलिखित बंटन एक मोहल्ले के बच्चों के दैनिक जेबखर्च दर्शाता है। माध्य जेबखर्च $₹18$ है। लुप्त बारंबारता $f$ ज्ञात कीजिए:View Solution
दैनिक जेब भत्ता $($रुपयों में$)$ $11-13$ $13-15$ $15-17$ $17-19$ $19-21$ $21-23$ $23-25$ बच्चों की संख्या $7$ $6$ $9$ $13$ $f$ $5$ $4$ - 3निम्नलिखित सारणी किसी मोहल्ले के $25$ परिवारों में भोजन पर हुए दैनिक व्यय को दर्शाती है:View Solution
एक उपयुक्त विधि द्वारा भोजन पर हुआ माध्य व्यय ज्ञात कीजिए।दैनिक व्यय $($रुपयों में$)$ $100-150$ $150-200$ $200-250$ $250-300$ $300-350$ परिवारों की संख्या $4$ $5$ $12$ $2$ $2$ - 4किसी स्कूल की कक्षा $X$ के $30$ विद्यार्थियों द्वारा गणित के एक पेपर में, $100$ में से प्राप्त किए गए अंक, नीचे एक सारणी में दिए गए हैं। इन विद्यार्थियों द्वारा प्राप्त अंकों का माध्य ज्ञात कीजिए।View Solution
प्राप्तांक $(x_i)$ $10$ $20$ $36$ $40$ $50$ $56$ $60$ $70$ $72$ $80$ $88$ $92$ $95$ विद्यार्थीयों की संख्या $(f_i)$ $1$ $1$ $3$ $4$ $3$ $2$ $4$ $4$ $1$ $1$ $2$ $3$ $1$ - 5View Solutionयदि नीचे दिए हुए बंटन का माध्यक 28.5 हो तो x और y के मान ज्ञात कीजिए:
वर्ग अंतराल बारंबारता 0 - 10 5 10 - 20 x 20 - 30 20 30 - 40 15 40 - 50 y 50 - 60 5 योग 60 - 6विद्यार्थियों के एक समूह द्वारा अपने पर्यावरण संचेतना अभियान के अंतर्गत एक सर्वेक्षण किया गया, जिसमें उन्होंने एक मोहल्ले के $20$ घरों में लगे हुए पौधों से संबंधित निम्नलिखित आँकड़े, एकत्रित किए। प्रति घर माध्य पौधों की संख्या ज्ञात कीजिए।View Solution
माध्य ज्ञात करने के लिए आपने किस विधि का प्रयोग किया और क्यों?पौधों की संख्या $0-2$ $2-4$ $4-6$ $6-8$ $8-10$ $10-12$ $12-14$ घरों की संख्या $1$ $2$ $1$ $5$ $6$ $2$ $3$ - 7वायु में सल्फर डाई$-$ऑक्साइड $(SO_2)$ की सांद्रता $($ भाग प्रति मिलियन में$)$ को ज्ञात करने के लिए, एक नगर के $30$ मोहल्लों से आँकड़े एकत्रित किए गए, जिन्हें नीचे प्रस्तुत किया गया है:View Solution
वायु में $SO_2$ की सांद्रता का माध्य ज्ञात कीजिए।$SO_2$ की सांद्रता बारंबारता $0.00 - 0.04$ $4$ $0.04 - 0.08$ $9$ $0.08 - 0.12$ $9$ $0.12 - 0.16$ $2$ $0.16 - 0.20$ $4$ $0.20 - 0.24$ $2$ - 8किसी अस्पताल में, एक डॉक्टर द्वारा $30$ महिलाओं की जाँच की गई और उनके हृदय स्पंदन $($beat$)$ की प्रति मिनट संख्या नोट करके नीचे दर्शाए अनुसार संक्षिप्त रूप में लिखी गई। एक उपयुक्त विधि चुनते हुए, इन महिलाओं के हृदय स्पंदन की प्रति मिनट माध्य संख्या ज्ञात कीजिए:View Solution
ह्रदय स्पंदन की प्रति मिनट संख्या $65-68$ $68-71$ $71-74$ $74-77$ $77-80$ $80-83$ $83-86$ महिलाओं की संख्या $2$ $4$ $3$ $8$ $7$ $4$ $2$ - 9View Solutionनिम्नलिखित आँकड़ों का माध्यक 525 है। यदि बारंबारताओं का योग 100 है, तो x और y का मान ज्ञात कीजिए।
वर्ग अंतराल बारंबारता 0 - 100 2 100 - 200 5 200 - 300 x 300 - 400 12 400 - 500 17 500 - 600 20 600 - 700 y 700 - 800 9 800 - 900 7 900 - 1000 4 - 10निम्नलिखित सारणी $35$ नगरों की साक्षरता दर $($प्रतिशत में$)$ दर्शाती है। माध्य साक्षरता दर ज्ञात कीजिए:View Solution
साक्षरता दर $(\%$ में$)$ $45-55$ $55-65$ $65-75$ $75-85$ $85-95$ नगरों की संख्या $3$ $10$ $11$ $8$ $3$