सिद्ध कीजिए कि किसी समतल में स्थित बिंदुओं के समुच्चय में, R = {(P, Q): बिंदु P की मूल बिंदु से दूरी, बिंदु Q की मूल बिंदु से दूरी के समान है द्वारा प्रदत्त संबंध R एक तुल्यता संबंध है। पुनः सिद्ध कीजिए कि बिंदु P $\neq(0,0)$ से संबंधित सभी बिंदुओं का समुच्चय P से होकर जाने वाले एक ऐसे वृत्त को निरूपित करता है, जिसका केंद्र मूलबिंदु पर है।
Exercise-1.1-11
R = {(P, Q) : बिंदु P की मूलबिंदु से दूरी, बिंदु Q की मूलबिंदु से दूरी के समान है}
चूँकि किसी बिंदु P की मूलबिंदु से दूरी, बिन्दु P की मूलबिंदु से दूरी के बराबर होती है। अतः (P, P$) \in R, \forall P \in$ A, अतः R, स्वतुल्य संबंध है। अब मान लीजिए (P, Q) $\in R$
$\Rightarrow$ बिन्दु P की मूलबिंदु से दूरी, बिंदु Q की मूलबिंदु से दूरी के बराबर है।
$\Rightarrow $ बिंदु Q की मूलबिंदु से दूरी, बिंदु P की मूलबिंदु से दूरी के बराबर है।
$\Rightarrow $ $(Q, P) \in R, \forall P, Q \in A $ अतः R, एक सममित संबंध है।
पुनः मान लीजिए
$(P, Q),(Q, S) \in P$
$\Rightarrow$ बिंदु P की मूलबिंदु से दूरी, बिंदु Q की मूलबिंदु से दूरी के बराबर है तथा बिंदु Q की मूलबिंदु से दूरी, बिंदु S की मूलबिंदु से दूरी के बराबर है।
$\Rightarrow$ बिंदु P की मूलबिंदु से दूरी, बिंदु S की मूलबिंदु से दूरी के बराबर है।
$\Rightarrow$ $(P, S) \in R$
अतः R एक संक्रमक संबंध है। अतः R, एक तुल्यता संबंध है। अब, बिंदु $P \neq(0,0)$ से संबंधित वह बिंदु हो, जिनकी मूलबिंदु से दूरी, बिंदु P की मूलबिंदु से दूरी के बराबर है अर्थात् यदि O(0, 0) मूलबिंदु है तथा OP = k, जहाँ k एक अचर है, तब बिंदु $P \neq(0,0)$ से संबंधित बिंदु, मूलबिंदु से अचर k दूरी पर होंगे। अतः बिंदु $P \neq(0,0)$ से संबंधित बिंदुओं का समुच्चय एक वृत्त है जिसका केन्द्र मूलबिंदु तथा यह वृत्त बिंदु P से होकर जाता है।
चूँकि किसी बिंदु P की मूलबिंदु से दूरी, बिन्दु P की मूलबिंदु से दूरी के बराबर होती है। अतः (P, P$) \in R, \forall P \in$ A, अतः R, स्वतुल्य संबंध है। अब मान लीजिए (P, Q) $\in R$
$\Rightarrow$ बिन्दु P की मूलबिंदु से दूरी, बिंदु Q की मूलबिंदु से दूरी के बराबर है।
$\Rightarrow $ बिंदु Q की मूलबिंदु से दूरी, बिंदु P की मूलबिंदु से दूरी के बराबर है।
$\Rightarrow $ $(Q, P) \in R, \forall P, Q \in A $ अतः R, एक सममित संबंध है।
पुनः मान लीजिए
$(P, Q),(Q, S) \in P$
$\Rightarrow$ बिंदु P की मूलबिंदु से दूरी, बिंदु Q की मूलबिंदु से दूरी के बराबर है तथा बिंदु Q की मूलबिंदु से दूरी, बिंदु S की मूलबिंदु से दूरी के बराबर है।
$\Rightarrow$ बिंदु P की मूलबिंदु से दूरी, बिंदु S की मूलबिंदु से दूरी के बराबर है।
$\Rightarrow$ $(P, S) \in R$
अतः R एक संक्रमक संबंध है। अतः R, एक तुल्यता संबंध है। अब, बिंदु $P \neq(0,0)$ से संबंधित वह बिंदु हो, जिनकी मूलबिंदु से दूरी, बिंदु P की मूलबिंदु से दूरी के बराबर है अर्थात् यदि O(0, 0) मूलबिंदु है तथा OP = k, जहाँ k एक अचर है, तब बिंदु $P \neq(0,0)$ से संबंधित बिंदु, मूलबिंदु से अचर k दूरी पर होंगे। अतः बिंदु $P \neq(0,0)$ से संबंधित बिंदुओं का समुच्चय एक वृत्त है जिसका केन्द्र मूलबिंदु तथा यह वृत्त बिंदु P से होकर जाता है।
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1एक अरिक्त समुच्चय X दिया हुआ है। P(X) जो कि X के समस्त उपसमुच्चयों का समुच्चय है, पर विचार कीजिए। निम्नलिखित तरह से P(X) में एक संबंध R परिभाषित कीजिए:View Solution
P(X) में उपसमुच्चयों A, B के लिए, ARB, यदि और केवल यदि A $\subset$ B है। क्या R, P(X) में एक तुल्यता संबंध है? अपने उत्तर का औचित्य भी लिखिए। - 2सिद्ध किजिए कि समुच्चय $\mathrm{A}=\{x \in \mathbf{Z}: 0 \leq x \leq 12\}$, में दिए गए निम्नलिखित संबंधों R में से प्रत्येक एक तुल्यता संबंध है:View Solution
- R = {(a, b) : |a - b|, 4 का एक गुणज है},
- R = {(a, b) : a = b},
प्रत्येक दशा में 1 से संबंधित अवयवों को ज्ञात कीजिए।
- 3यदि $f : R \rightarrow R$ जहाँ $f(x) = x^2- 3x + 2$ द्वारा परिभाषित, है, तो $f(f(x))$ ज्ञात कीजिए।View Solution
- 4a * b = |a - b| तथा a o b = a, $\forall$ a, b $\in$ R द्वारा परिभाषित द्विआधारी संक्रियाओं *: R $\times$ R $ \rightarrow $ R तथा o : R $\times$ R $\rightarrow $ R पर विचार कीजिए। सिद्ध कीजिए कि * क्रमविनिमेय है परंतु साहचर्य नहीं है, o साहचर्य है परंतु क्रमविनिमेय नहीं है। पुनः सिद्ध कीजिए कि सभी a, b, c $\in $ R के लिए a * (b o c) = (a * b) o (a * c) है। [यदि ऐसा होता है, तो हम कहते हैं कि संक्रिया * संक्रिया o पर वितरित (Distributes) होती है।] क्या o संक्रिया * पर वितरित होती है? अपने उत्तर का औचित्य भी बतलाइए।View Solution
- 5View Solutionसिद्ध कीजिए कि किसी कॉलेज के पुस्तकालय की समस्त पुस्तकों के समुच्चय A में R = {(x, y): x तथा y में पेजों की संख्या समान है} द्वारा प्रदत्त संबंध R एक तुल्यता संबंध है।
- 6निम्नलिखित प्रकार से समुच्चय $\{0, 1, 2, 3, 4, 5\}$ में एक द्विआधारी संक्रिया $^*$ परिभाषित कीजिएView Solution
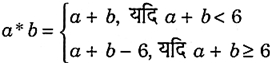
सिद्ध कीजिए कि शून्य $(0)$ इस संक्रिया का तत्समक है तथा समुच्चय का प्रत्येक अवयव $a \neq0$ व्युत्क्रमणीय है, इस प्रकार कि $6 - a, a$ का प्रतिलोम है। - 7सिद्ध कीजिए कि R में $\mathrm{R}=\{(a, b): a \leq b\}$, द्वारा परिभाषित संबंध R स्वतुल्य तथा संक्रामक है किंतु सममित नहीं है।View Solution
- 8मान लीजिए कि $A = {-1, 0, 1, 2}, B = {- 4, -2, 0, 2}$ और $f, g : A \rightarrow B,$ क्रमशः $f(x) = x^2- x, x \in A$ तथा $g(x) = 2\left|x-\frac{1}{2}\right|-1, x \in A$ द्वारा परिभाषित फलन हैं। क्या $f$ तथा $g$ समान हैं? अपने उत्तर का औचित्य भी बतलाइए।View Solution
- 9जाँच कीजिए कि क्या समुच्चय {1, 2, 3, 4, 5, 6} में $\mathrm{R}=\{(a, b): b=a+1\}$ द्वारा परिभाषित संबंध R स्वतुल्य, सममित या संक्रामक है।View Solution
- 10सिद्ध कीजिए कि समस्त त्रिभुजों के समुच्चय $A$ में, $\mathrm{R}=\left\{\left(\mathrm{T}_{1}, \mathrm{~T}_{2}\right): \mathrm{T}_{1}, \mathrm{~T}_{2}\right.$ के समरूप है द्वारा परिभाषित संबंध $R$ एक तुल्यता संबंध है। भुजाओं $3, 4, 5$ वाले समकोण त्रिभुज $T_1,$ भुजाओं $5, 12, 13$ वाले समकोण त्रिभुज $T_2$ तथा भुजाओं $6, 8, 10$ वाले समकोण त्रिभुज $T_3$ पर विचार कीजिए। $\mathrm{T}_{1}, \mathrm{~T}_{2}$ और $T_{3 }$ में से कौन से त्रिभुज परस्पर संबंधित हैं?View Solution
