त्रिभुज की भुजाओं से a और b दूरी पर त्रिभुज के कर्ण पर स्थित एक बिंदु है। सिद्ध कीजिए कि कर्ण की न्यूनतम लंबाई $ \left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)^{\frac{1}{2}}$ है।
Miscellaneous Exercise-12
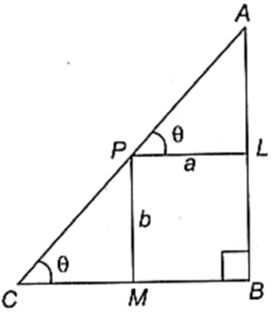
मान लीजिए समकोण $\triangle $ABC के कर्ण AC में P एक बिंदु इस प्रकार है कि
PL $\perp$ AB = a और PM $\perp $ BC = b
पुनः मान लीजिए
$\angle A P L$ = $ \angle A C B$ = $\theta $
AP = asec $\theta $, PC = b $\operatorname{cosec} \theta $
पुनः मान लीजिए कि कर्ण की लंबाई I है, तब
l = AP + PC $\Rightarrow$ l = a sec $\theta $ + b $\operatorname{cosec} \theta$, 0 < $\theta$ < $ \frac{\pi}{2} $
$\theta$ के सापेक्ष अवकलन करने पर,
$\frac{d l}{d \theta}$ = $a \sec \theta \tan \theta$ - $b \operatorname{cosec} \theta \cot \theta$
उच्चतम और निम्नतम मान के लिए $\frac{d l}{d \theta}$ = 0 रखने पर
$\Rightarrow$ asec $\theta \tan \theta$ = b $b\operatorname{cosec} \theta \cot \theta$
$\Rightarrow$ $\frac{a \sin \theta}{\cos ^{2} \theta}$ = $\frac{b \cos \theta}{\sin ^{2} \theta} $ $\Rightarrow $ $\frac{\sin ^{3} \theta}{\cos ^{3} \theta}$ = $\frac{b}{a}$
$ \Rightarrow$ $\tan ^{3} \theta$ = $\frac{b}{a}$ $ \Rightarrow$ $ \tan \theta$ $\left(\frac{b}{a}\right)^{1 / 3} $
अब, $\frac{d^{2} l}{d \theta^{2}}$ = a $\left(\sec \theta \times \sec ^{2} \theta+\tan \theta \times \sec \theta \tan \theta\right)$ - b $\left[\operatorname{cosec} \theta\left(-\operatorname{cosec}^{2} \theta\right)+\cot \theta(-\operatorname{cosec} \theta \cot \theta)\right]$
= a $\sec \theta$ $ \left(\sec ^{2} \theta+\tan ^{2} \theta\right)$ + b $ \operatorname{cosec}$ $ \theta$ $\left(\operatorname{cosec}^{2} \theta+\cot ^{2} \theta\right)$
चूँकि 0 < $\theta$ < $ \frac{\pi}{2}$ है इसलिए त्रिकोणमितीय अनुपात धनात्मक होंगे
और a > 0, b > 0
$\therefore$ $ \frac{d^{2} l}{d \theta^{2}}$ धनात्मक है।
$\Rightarrow$ जब $\tan \theta$ = $ \left(\frac{b}{a}\right)^{1 / 3}$ हो, तो I न्यूनतम है।
$\therefore$ l का न्यूनतम मान = a sec $ \theta$ + $b \operatorname{cosec} \theta$
= a $ \frac{\sqrt{a^{2 / 3}+b^{2 / 3}}}{a^{1 / 3}}$+ b$ \frac{\sqrt{a^{2 / 3}+b^{2 / 3}}}{b^{1 / 3}}$
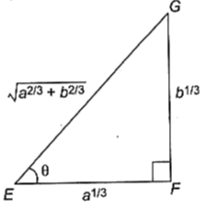
= $\sqrt{a^{2 / 3}+b^{2 / 3}}$ $\left(a^{2 / 3}+b^{2 / 3}\right)$= $\left(a^{2 / 3}+b^{2 / 3}\right)^{3 / 2} $ [$\because$ $\Delta$ EFG में, sec $\theta$ = $ \frac{\sqrt{a^{2 / 3}+b^{2 / 3}}}{a^{1 / 3}}$ तथा $ \operatorname{cosec} \theta$ = $\frac{\sqrt{a^{2 / 3}+b^{2 / 3}}}{b^{1 / 3}}$]
PL $\perp$ AB = a और PM $\perp $ BC = b
पुनः मान लीजिए
$\angle A P L$ = $ \angle A C B$ = $\theta $
AP = asec $\theta $, PC = b $\operatorname{cosec} \theta $
पुनः मान लीजिए कि कर्ण की लंबाई I है, तब
l = AP + PC $\Rightarrow$ l = a sec $\theta $ + b $\operatorname{cosec} \theta$, 0 < $\theta$ < $ \frac{\pi}{2} $
$\theta$ के सापेक्ष अवकलन करने पर,
$\frac{d l}{d \theta}$ = $a \sec \theta \tan \theta$ - $b \operatorname{cosec} \theta \cot \theta$

उच्चतम और निम्नतम मान के लिए $\frac{d l}{d \theta}$ = 0 रखने पर
$\Rightarrow$ asec $\theta \tan \theta$ = b $b\operatorname{cosec} \theta \cot \theta$
$\Rightarrow$ $\frac{a \sin \theta}{\cos ^{2} \theta}$ = $\frac{b \cos \theta}{\sin ^{2} \theta} $ $\Rightarrow $ $\frac{\sin ^{3} \theta}{\cos ^{3} \theta}$ = $\frac{b}{a}$
$ \Rightarrow$ $\tan ^{3} \theta$ = $\frac{b}{a}$ $ \Rightarrow$ $ \tan \theta$ $\left(\frac{b}{a}\right)^{1 / 3} $
अब, $\frac{d^{2} l}{d \theta^{2}}$ = a $\left(\sec \theta \times \sec ^{2} \theta+\tan \theta \times \sec \theta \tan \theta\right)$ - b $\left[\operatorname{cosec} \theta\left(-\operatorname{cosec}^{2} \theta\right)+\cot \theta(-\operatorname{cosec} \theta \cot \theta)\right]$
= a $\sec \theta$ $ \left(\sec ^{2} \theta+\tan ^{2} \theta\right)$ + b $ \operatorname{cosec}$ $ \theta$ $\left(\operatorname{cosec}^{2} \theta+\cot ^{2} \theta\right)$
चूँकि 0 < $\theta$ < $ \frac{\pi}{2}$ है इसलिए त्रिकोणमितीय अनुपात धनात्मक होंगे
और a > 0, b > 0
$\therefore$ $ \frac{d^{2} l}{d \theta^{2}}$ धनात्मक है।
$\Rightarrow$ जब $\tan \theta$ = $ \left(\frac{b}{a}\right)^{1 / 3}$ हो, तो I न्यूनतम है।
$\therefore$ l का न्यूनतम मान = a sec $ \theta$ + $b \operatorname{cosec} \theta$
= a $ \frac{\sqrt{a^{2 / 3}+b^{2 / 3}}}{a^{1 / 3}}$+ b$ \frac{\sqrt{a^{2 / 3}+b^{2 / 3}}}{b^{1 / 3}}$

= $\sqrt{a^{2 / 3}+b^{2 / 3}}$ $\left(a^{2 / 3}+b^{2 / 3}\right)$= $\left(a^{2 / 3}+b^{2 / 3}\right)^{3 / 2} $ [$\because$ $\Delta$ EFG में, sec $\theta$ = $ \frac{\sqrt{a^{2 / 3}+b^{2 / 3}}}{a^{1 / 3}}$ तथा $ \operatorname{cosec} \theta$ = $\frac{\sqrt{a^{2 / 3}+b^{2 / 3}}}{b^{1 / 3}}$]
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1सिद्ध कीजिए कि एक $r$ त्रिज्या के गोले के अंतर्गत उच्चतम आयतन के लंबवृत्तीय शंकु की ऊँचाई $\frac{4 r}{3}$ है।View Solution
- 2$100 \ cm^3$ आयतन वाले डिब्बे सभी बंद बेलनाकार $($लंब वृत्तीय$)$ डिब्बों में से न्यूनतम पृष्ठ क्षेत्रफल वाले डिब्बे की विमाएँ ज्ञात किजिए।View Solution
- 3View Solution2 m ऊँचाई का आदमी 6 m ऊँचे बिजली के खंभे से दूर 5 km/ h की समान चाल से चलता है। उसकी छाया की लंबायीं की वृद्धि दर ज्ञात कीजिए।
- 4$18 \ cm$ भुजा के टिन के किसी वर्गाकार टुकड़े से प्रत्येक कोने पर एक वर्ग काटकर तथा इस प्रकार बने टिन के फलकों को मोड़ कर ढक्कन रहित एक संदूक बनाना है। काटे जाने वाले वर्ग की भजा कितनी होगी जिससे संदक का आयतन उच्चतम हो?View Solution
- 5एक कार समय $t = 0$ पर बिंदु $P$ से चलना प्रारंभ करके बिंदु $Q$ पर रुक जाती है। कार द्वारा $t$ सेकंड में तय की दूरी$, x$ मीटर में $x = t^2 \left(2-\frac{t}{3}\right)$ द्वारा प्रदत्त है। कार को $Q$ तक पहुँचने में लगा समय ज्ञात कीजिए और $P$ तथा $Q$ के बीच की दूरी भी ज्ञात कीजिए।View Solution
- 6View Solutionएक वृत्त और एक वर्ग के परिमापों का योग k है, जहाँ k एक अचर है। सिद्ध कीजिए कि उनके क्षेत्रफलों का योग निम्नतम है, जब वर्ग की भुजा वृत्त की त्रिज्या की दुगुनी है।
- 7सिद्ध कीजिए कि $R$ त्रिज्या के गोले के अंतर्गत विशालतम शंकु का आयतन, गोले के आयतन का $\frac{8}{27}$ होता है।View Solution
- 8ऐल्यूमिनियम की $3m \times 8 m$ की आयताकार चादर के प्रत्येक कोने से समान वर्ग काटने पर बने एल्यूमिनियम के फलकों को मोड़कर ढक्कन रहित एक संदूक बनाना है। इस प्रकार बने संदूक का अधिकतम आयतन ज्ञात कीजिए।View Solution
- 9सिद्ध कीजिए कि दी हुई तिर्यक ऊँचाई और महत्तम आयतन वाले शंकु का अर्ध शीर्ष कोण $\tan ^{-1}\sqrt{2}$ होता है।View Solution
- 10$45$ सेमी $\times\ 24$ सेमी की टिन की आयताकार चादर के कोनों पर वर्ग काटकर तथा इस प्रकार बनें टिन के फलकों को मोड़कर ढ़क्कन रहित एक संदूक बनाना है। काटे जाने वाले वर्ग की भुजा कितनी होगी जिससे संदूक का आयतन उच्चतम हो।View Solution
