त्रिघात बहुपद $x^{3}-3 \sqrt{5} x^{2}+13 x-3 \sqrt{5}$ का एक गुणनखंड $x-\sqrt{5}$ दिया है। इस बहुपद के सभी शून्यक ज्ञात कीजिए।
Exercise-2.4-5
Download our app for free and get started
माना दिए गए बहुपद f(x) = $x^{3}-3 \sqrt{5} x^{2}+13 x-3 \sqrt{5}$ और g(x) = $(x-\sqrt{5})$
$\because$ g(x) f(x) का एक गुणनखंड है इसलिए f(x) = q(x) $(x-\sqrt{5})$
यूक्लिड का विभाजन एल्गोरिथ्म द्वारा
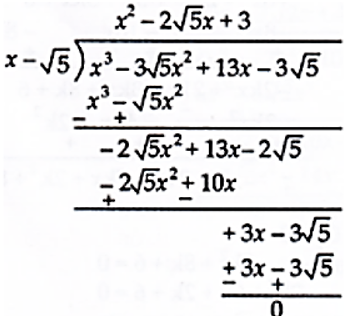
लेकिन, f(x) = q(x) g(x)
$\therefore$ f(x) = $\left(x^{2}-2 \sqrt{5} x+3\right)(x-\sqrt{5})$
$\Rightarrow$ f(x) = $\left[x^{2}-\{(\sqrt{5}+\sqrt{2})+(\sqrt{5}-\sqrt{2})\} x\right.$ + $(\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2})][(x-\sqrt{5})]$
= $x[x-(\sqrt{5}+\sqrt{2})]-(\sqrt{5}-\sqrt{2})$ $[x-(5+\sqrt{2})][x-\sqrt{5}]$ f(x) के शून्यकों के लिए, f(x) = 0
$\Rightarrow$ $(x-\sqrt{5}-\sqrt{2})(x-\sqrt{5}+\sqrt{2})(x-\sqrt{5})$ = 0
$\Rightarrow$ $(x-\sqrt{5}-\sqrt{2})$ = 0 या $(x-\sqrt{5}+\sqrt{2})$ = 0 या $(x-\sqrt{5})$ = 0
$\Rightarrow$ x = $\sqrt{5}+\sqrt{2}$ या x = $\sqrt{5}-\sqrt{2}$ या x = $\sqrt{5}$
अत: दिए गए बहुपद के शून्यक हैं $(\sqrt{5}+\sqrt{2}),(\sqrt{5}-\sqrt{2})$ तथा $\sqrt{5}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1दिया है कि त्रिघात बहुपद $x^3 - 6x^2 + 3x + 10$ के शून्यक $a, a + b$ और $a + 2b$ के रूप के हैं, जहाँ $a$ और$ b,$ कोई वास्तविक संख्याएँ हैं। $a$ और $b$ के मान तथा साथ ही दिए हुए बहुपद के शून्यक ज्ञात कीजिए।View Solution
- 2यदि एक त्रिघात बहुपद $x^3 + ax^2 - bx + c$ के तीनों शून्यक धनात्मक हैं, तो $a, b$ और $c$ में से कम से कम एक अवश्य ही ऋणेतर होगा।View Solution
- 3$\frac{-8}{3}, \frac{4}{3}$ में बहुपद ज्ञात कीजिए, जिनके शून्यकों के क्रमशः योग और गुणनफल दिए हुए हैं। साथ ही, गुणनखंडन द्वारा, इन बहुपदों के शून्यक भी ज्ञात कीजिए।View Solution
- 4यदि $x^3 + 2x^2 + kx + 3$ को $x - 3$ से भाग देने पर शेषफल $21$ प्राप्त होता है, तो $k$ का मान और भागफल ज्ञात कीजिए। इसके बाद, त्रिघात बहुपद $x^3 + 2x^2 + kx - 18$ के शून्यक ज्ञात कीजिए।View Solution
- 5त्रिघात बहुपद $6 x^{3}+\sqrt{2} x^{2}-10 x-4 \sqrt{2}$ का एक शून्यक $\sqrt{2}$ दिया है। इसके अन्य दो शून्यक ज्ञात कीजिए।View Solution
- 6$a$ और $b$ के किन मानों के लिए, $q(x) = x^3 + 2x^2 + a$ के शून्यक बहुपद$ p(x) = x^5 - x^4 - 4x^3 + 3x^2 + 3x + b$ के भी शून्यक होंगे? $p(x)$ के कौन से शून्यक $q(x)$ के शून्यक नहीं हैं?View Solution
- 7$-2 \sqrt{3}, -9$ में बहुपद ज्ञात कीजिए, जिनके शून्यकों के क्रमशः योग और गुणनफल दिए हुए हैं। साथ ही, गुणनखंडन द्वारा, इन बहुपदों के शून्यक भी ज्ञात कीजिए।View Solution
- 8View Solutionयदि एक त्रिघात बहुपद के सभी शून्यक ऋणात्मक हैं, तो इस बहुपद के सभी गुणांक और अचर पद एक ही चिह्न के होते हैं।
- 9View Solutionयदि एक शून्येतर बहुपद p(x) को एक बहुपद g(x) से भाग देने पर शेषफल 0 हो, तो p(x) और g(x) की घातों में क्या संबंध है?
- 10View Solutionयदि एक त्रिघात बहुपद के दो शून्यकों में से प्रत्येक शून्य है, तो इसके रैखिक और अचर पद नहीं हो सकते।