त्रिज्या $8 \ cm$ और ऊँचाई $12 \ cm$ वाले एक शंकु को उसकी अक्ष के मध्य$-$बिंदु से होकर जाने वाले और आधार के समांतर तल द्वारा दो भागों में विभाजित किया जाता है। दोनों भागों के आयतनों का अनुपात ज्ञात कीजिए।
Exercise-12.3-4
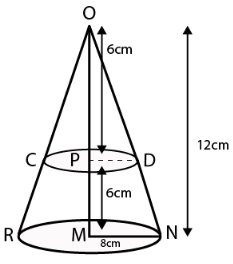
प्रश्न के अनुसार, शंकु की ऊँचाई $= OM = 12 \ cm$
शंकु को मध्य-बिंदु से विभाजित किया जाता है।
अतः माना शंकु का मध्य-बिंदु $= P$
$OP = PM = 6 \ cm$
से $\triangle OPD$ और $\triangle OMN$
$\angle POD = \angle POD [$सामान्य$]$
$\angle OPD = \angle OMN [$दोनों $90^\circ ]$
इसलिए, कोण$-$कोण समानता मानदंड से हमारे पास है,
$\triangle OPD \sim \triangle OMN$
और
समरूप त्रिभुजों की संगत भुजाएँ समान अनुपात में होती हैं,
इसलिए, हमारे पास, $\frac {PD}{MN} = \frac {OP}{OM}$
$\frac {PD}8 = \frac 6{12}$
$PD = 4\ cm [MN = 8 \ cm =$ शंकु के आधार की त्रिज्या$]$
पहले भाग के लिए अर्थात् शंकु
आधार त्रिज्या, $r = PD = 4 \ cm$
ऊँचाई, $h = OP = 6 \ cm$
हम जानते हैं कि, त्रिज्या$ r$ और ऊँचाई h,
शंकु का आयतन $V = \frac 13 \pi r^2h$
पहले भाग का आयतन $= \frac 13 \pi (4)^2 6 = 32\pi$
दूसरे भाग के लिए, अर्थात् छिन्नक की
निचली त्रिज्या, $r_1 = MN = 8 \ cm$
शीर्ष त्रिज्या, $r_2 = PD = 4 \ cm$
ऊँचाई,$ h = PM = 6 \ cm$
हम जानते हैं कि,
शंकु के छिन्नक का आयतन $= \frac 13 \pi h\left(r_{1}^{2}+r_{2}^{2}+r_{1} r_{2}\right),$
जहाँ $h = $ ऊँचाई, $r_1$ और $r_2$ त्रिज्याएँ हैं, $(r_1 > r_2)$
दूसरे भाग का आयतन $= \frac 13 \pi(6) [8^2 + 4^2 + 8(4)]$
$= 2\pi(112) = 224\pi$
इसलिए, हमें अनुपात मिलता है,
शंकु का आयतन : शंकु के छिन्नक का आयतन
$= 32\pi : 224\pi = 1 : 7$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1एक $7 \ cm$ व्यास वाले बेलनाकार बीकर, जिसमें कुछ पानी भरा है, में $1.4 \ cm$ व्यास वाले कंचे डाले जाते हैं। कंचों की वह संख्या ज्ञात कीजिए जिनको बीकर में डालने से पानी का स्तर $5.6 \ cm$ ऊपर उठ जायेगा।View Solution
- 2किसी धातु के तीन घनों, जिनके किनारे $3:4:5$ के अनुपात में हैं, को पिघलाकर एक अकेले घन के रूप में बदला जाता है, जिसका विकर्ण $12\sqrt{3}\ cm$ है। तीनों घनों के किनारे ज्ञात कीजिए।View Solution
- 3कोई नहर $300 \ cm$ चौड़ी और $120 \ cm$ गहरी है। इस नहर में पानी $20 \ km/h$ की चाल से बह रहा है। वह $20$ मिनट में कितने क्षेत्रफल की सिंचाई करेगी, यदि इसके लिए $8 \ cm$ खड़े पानी की आवश्यकता होती है?View Solution
- 4View Solutionविमाओं 66 cm, 42 cm और 21 cm वाले एक ठोस घनाभाकार सीसे के टुकड़े में से 4.2 cm वाली कितनी सीसे की गोलियाँ प्राप्त की जा सकती हैं?
- 5समान आधार त्रिज्या $8 \ cm$ और समान ऊँचाई $15 \ cm$ वाले दो शंकुओं को उनके आधारों के अनुदिश जोड़ा जाता है। इस प्रकार बने आकार का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।View Solution
- 6$24 m$ लंबी, $0.4 m$ मोटी और $6 m$ ऊँची एक दीवार का ईंटों से निर्माण कराया जाता है, जिनमें से प्रत्येक ईंट की विमाएँ $25 \ cm \times 16 \ cm \times 10 \ cm $ हैं। यदि दीवार के आयतन का $\frac{1}{10}$ भाग मसाले से भरा जाता है, तो दीवार के निर्माण में लगने वाली ईंटों की संख्या ज्ञात कीजिए।View Solution
- 7एक $44 \ cm$ किनारे वाले सीसे के ठोस घन में से $4 \ cm$ व्यास वाली कितनी सीसे की गोलियाँ बनायी जा सकती हैं?View Solution
- 8आधार व्यास $1.5 \ cm$ और ऊँचाई $0.2 \ cm$ वाली धातु की वृत्ताकार चकतियों की संख्या ज्ञात कीजिए जिनको पिघलाकर $10 \ cm$ ऊँचाई और $4.5 \ cm$ व्यास का एक ठोस लंब वृत्तीय बेलन बनाया जा सके।View Solution
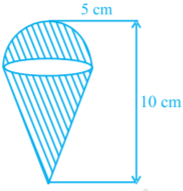
- 9आकृति में, एक आइसक्रीम शंकु दर्शाया गया है, जिसमें आइसक्रीम भरी हुई है, तथा इसकी त्रिज्या $5 \ cm$ और ऊँचाई $10 \ cm$ है। आइसक्रीम का आयतन ज्ञात कीजिए, जबकि शंकु का $\frac{1}{6}$ भाग आइसक्रीम से रिक्त रहता है।View Solution
- 10विमाओं $9 \ cm \times 11 \ cm \times 12 \ cm$ वाले एक सीसे के घनाभाकार ठोस से $3 \ cm$ व्यास वाली कितनी गोलियाँ बनायी जा सकती हैं?View Solution
