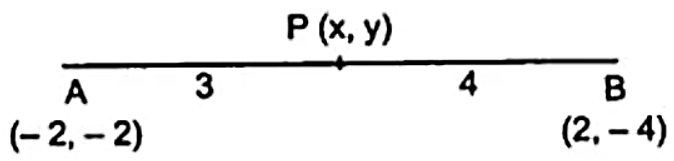
यहाँ दिए गये बिन्दु हैं: A(-2, -2) और B(2, -4) माना रेखाखण्ड AB को बिन्दु P इस प्रकार विभाजित करता है कि:
AP = $\frac{3}{7}$AB या $\frac{\mathrm{AP}}{\mathrm{AB}}=\frac{3}{7}$
$\Rightarrow$ $\frac{\mathrm{AP}+\mathrm{BP}}{\mathrm{AP}}=\frac{7}{3}$
$\Rightarrow$ $1+\frac{B P}{A P}=\frac{3+4}{3}=1+\frac{4}{3}$
$\Rightarrow$ $\frac{B P}{A P}=\frac{4}{3} \Rightarrow$ AP : PB = 3 : 4
i.e., P(x, y) AB को 3 : 4 के अनुपात में विभाजित करता है।
$\therefore$ x = $\frac{3 \times 2+4 \times(-2)}{3+4}=\frac{6-8}{7}=\frac{-2}{7}$
y = $\frac{3 \times(-4)+4 \times(-{2})}{3+4}$
= $\frac{-12-8}{7}=\frac{-20}{7}$
इस प्रकार, P के निर्देशांक हैं: $\left(\frac{-2}{7}, \frac{-20}{7}\right)$
Download our appand get started for free
Similar Questions
- 1View Solution
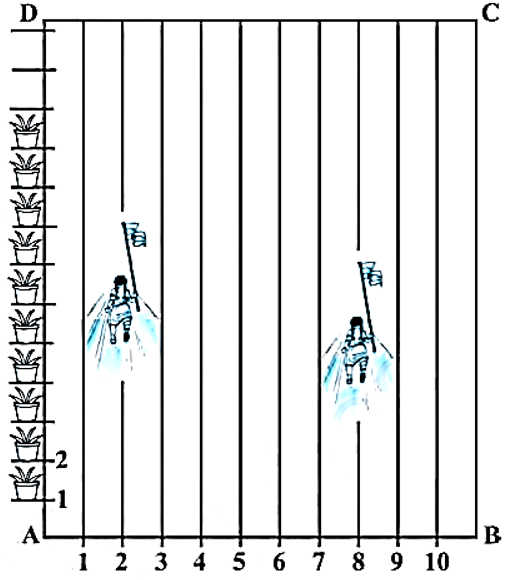
आपके स्कूल में खेल-कूद क्रियाकलाप आयोजित करने के लिए, एक आयताकार मैदान ABCD में, चूने से परस्पर 1 m की दूरी पर पंक्तियाँ बनाई गई हैं। AD के अनुदिश परस्पर 1 m की दूरी पर 100 गमले रखे गए हैं, जैसा कि आकृति में दर्शाया गया है। निहारिका दूसरी पंक्ति में AD के $\frac{1}{4}$ भाग के बराबर की दूरी दौड़ती है और वहाँ एक हरा झंडा गाड़ देती है। प्रीत आठवीं पंक्ति में AD के $\frac{1}{5}$ भाग के बराबर की दूरी दौड़ती है और वहाँ एक लाल झंडा गाड़ देती है। दोनों झंडों के बीच की दूरी क्या है? यदि रश्मि को एक नीला झंडा इन दोनों झंडों को मिलाने वाले रेखाखंड पर ठीक आधी दूरी (बीच में) पर गाड़ना हो तो उसे अपना झंडा कहाँ गाड़ना चाहिए?
- 2बिंदुओं $A(-2, 2)$ और $B(2, 8)$ को जोड़ने वाले रेखाखंड $AB$ को चार बराबर भागों में विभाजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए।View Solution
- 3View Solutionवह अनुपात ज्ञात कीजिए जिसमें बिंदुओं A(1, -5) और B(-4, 5) को मिलाने वाला रेखाखंड x-अक्ष से विभाजित होता है। इस विभाजन बिंदु के निर्देशांक भी ज्ञात कीजिए।
- 4बिंदुओं $(-3, 10)$ और $(6, -8)$ को जोड़ने वाले रेखाखंड को बिंदु $(-1, 6)$ किस अनुपात में विभाजित करता है।View Solution
- 5View Solutionबिंदु A के निर्देशांक ज्ञात कीजिए, जहाँ AB एक वृत्त का व्यास है जिसका केंद्र (2, -3) है तथा B के निर्देशांक (1, 4) हैं।
- 6एक समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष, इसी क्रम में, (3, 0), (4, 5), (-1, 4) और (-2, -1) हैं। [संकेत : समचतुर्भुज का क्षेत्रफल = $\frac{1}{2}$ (उसके विकर्णों का गुणनफल)]View Solution
- 7$y-$अक्ष पर एक ऐसा बिंदु ज्ञात कीजिए, जो बिंदुओं $A(6, 5)$ और $B(-4, 3)$ से समदूरस्थ हो।View Solution
- 8View Solution
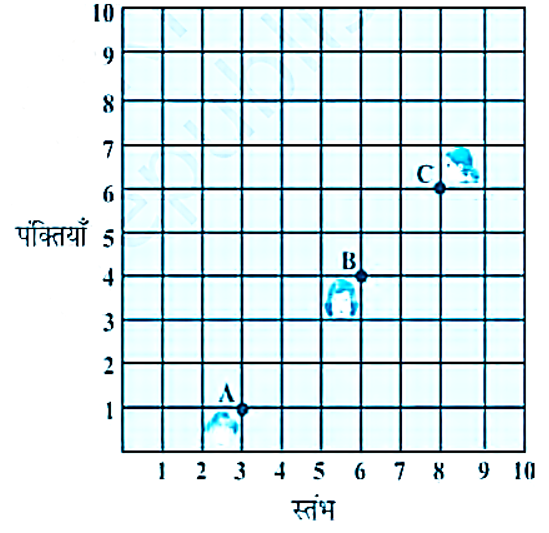
आकृति में किसी कक्षा में रखे डेस्कों (desks) की व्यवस्था दर्शाती है। आशिमा, भारती और कैमिला क्रमशः A(3, 1), B(6, 4) और C(8, 6) पर बैठी हैं। क्या आप सोचते हैं कि वे एक ही सीध (in a line) में बैठी हैं? सकारण उत्तर दीजिए।
- 9View Solutionदर्शाइए कि बिंदु (1, 7), (4, 2), (-1, -1) और (-4, 4) एक वर्ग के शीर्ष हैं।
- 10View Solutionबिंदुओं (4, -1) और (-2, -3) को जोड़ने वाले रेखाखंड को सम-त्रिभाजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए।
