यदि किसी $AP$ के प्रथम $6$ पदों का योग $36$ है तथा प्रथम $16$ पदों का योग $256$ है, तो उसके प्रथम $10$ पदों का योग ज्ञात कीजिए।
Exercise-5.3-28
$AP$ पर विचार करें जिसका पहला पद और सार्व अंतर क्रमशः $'a\ '$ और $'d\ '$ है।
यदि किसी $AP$ के पहले $6$ पदों का योग $36$ है।
$S_6 = 36$
$\therefore \frac 62 [2a + (6 – 1)d] = 36 [\because S_n = \frac n2 [2a + (n - 1)d]$
$\Rightarrow 3[2a + 5d] = 36$
$\Rightarrow 2a + 5d = \frac {36}3$
$\Rightarrow 2a + 5d = 12 …(i)$
यदि पहले $16$ पदों का योग $256$ है,
तो, $S_{16} = 256$
$\Rightarrow \frac {16}2 [2a + (16 - 1)d = 256$
$\Rightarrow 8[2a + 15d] = 256$
$\Rightarrow 2a + 15d = \frac {256}8$
$\Rightarrow 2a + 15d = 32 …(ii)$
$(i)$ को $(ii)$ से घटाने पर, हमें प्राप्त होता है
$2a + 15d = 32 ...(ii)$
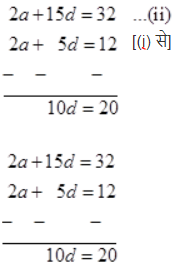
$\Rightarrow d = 2$
अब, $2a + 5d = 12 [(i)$ से $]$
$\Rightarrow 2a + 5(2) = 12$
$\Rightarrow 2a + 10 = 12$
$\Rightarrow 2a = 12 - 10$
$\Rightarrow a = \frac 22$
$\Rightarrow a = 1$
$\therefore a = 1$ और $d = 2$
$S_{10} = \frac {10}2[2a + (10 - 1)d$
$= 5[2(1) + 9(2)]$
$= 5[2 + 18]$
$= 5[20]$
$= 100$
$\Rightarrow S_{10} = 100$
अत: प्रथम $10$ पदों का योग $100$ है।
यदि किसी $AP$ के पहले $6$ पदों का योग $36$ है।
$S_6 = 36$
$\therefore \frac 62 [2a + (6 – 1)d] = 36 [\because S_n = \frac n2 [2a + (n - 1)d]$
$\Rightarrow 3[2a + 5d] = 36$
$\Rightarrow 2a + 5d = \frac {36}3$
$\Rightarrow 2a + 5d = 12 …(i)$
यदि पहले $16$ पदों का योग $256$ है,
तो, $S_{16} = 256$
$\Rightarrow \frac {16}2 [2a + (16 - 1)d = 256$
$\Rightarrow 8[2a + 15d] = 256$
$\Rightarrow 2a + 15d = \frac {256}8$
$\Rightarrow 2a + 15d = 32 …(ii)$
$(i)$ को $(ii)$ से घटाने पर, हमें प्राप्त होता है
$2a + 15d = 32 ...(ii)$
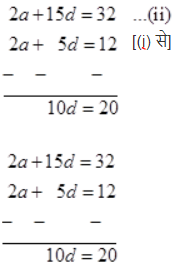
$\Rightarrow d = 2$
अब, $2a + 5d = 12 [(i)$ से $]$
$\Rightarrow 2a + 5(2) = 12$
$\Rightarrow 2a + 10 = 12$
$\Rightarrow 2a = 12 - 10$
$\Rightarrow a = \frac 22$
$\Rightarrow a = 1$
$\therefore a = 1$ और $d = 2$
$S_{10} = \frac {10}2[2a + (10 - 1)d$
$= 5[2(1) + 9(2)]$
$= 5[2 + 18]$
$= 5[20]$
$= 100$
$\Rightarrow S_{10} = 100$
अत: प्रथम $10$ पदों का योग $100$ है।
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1किसी $AP$ में यदि $S_{n }= 3n^{2 }+ 5n$ और $a_{k }= 164$ है, तो $k$ का मान ज्ञात कीजिए।View Solution
- 2वह $AP$ निर्धारित कीजिए जिसका पाँचवाँ पद $19$ है तथा आठवें पद का तेरहवें पद से अंतर $20$ है।View Solution
- 3$AP: -15, -13, -11, ...$ का योग $-55$ बनाने के लिए इसके कितने पदों की आवश्यकता होगी? दो उत्तर प्राप्त होने का कारण स्पष्ट कीजिए।View Solution
- 4यदि $a_{n }= 3 - 4n$ हो, तो दर्शाइए कि $a_1, a_2, a_3, ...$ एक $AP$ बनाते हैं। $S_{20}$ भी ज्ञात कीजिए।View Solution
- 5View Solutiona, b और c के ऐसे मान ज्ञात कीजिए कि संख्याएँ a, 7, b, 23, c एक AP में हों।
- 6View Solutionयदि संख्याएँ n - 2, 4n - 1 और 5n + 2 किसी AP में हैं, तो n का मान ज्ञात कीजिए।
- 7ऐसी प्रथम सात संख्याओं का योग ज्ञात कीजिए, जो $2$ का गुणज हैं और $9$ का भी गुणज हैं।View Solution
- 8योग ज्ञात कीजिए: $4-\frac 1n + 4-\frac 2n + 4-\frac 3n + ...n$ पदों तकView Solution
- 9प्रथम पद $8$ और सार्व अंतर $20$ वाली एक $AP$ के प्रथम $n$ पदों का योग एक अन्य $AP$ के प्रथम $2n$ पदों के योग के बराबर है, जिसका प्रथम पद $-30$ और सार्व अंतर $8$ है। $n$ ज्ञात कीजिए।View Solution
- 10यदि किसी $AP$ का $9$वाँ पद शून्य है, तो सिद्ध कीजिए कि उसका $29$वाँ पद उसके $19$वें पद का दुगुना होगा।View Solution
