Question Bank
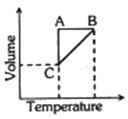
Explore our large set of questions to practice for your standard seamlessly- 1કોઈ વાયુના પાંચ મોલને શ્રેણીમાં થતા ફેરફારના ઘટનાક્રમમાં મૂકવામાં આવેલ છે. જે નીચે આપેલા આલેખ વડે દર્શાવી શકાય છે, તો આ આલેખમાં $A$ $\rightarrow$ $B$, $B$ $\rightarrow$ $C$ અને $C$ $\rightarrow$ $A$ અનુક્રમે શું હશે ?View Solution
- 2કોષના પ્રમાણિત $e.m.f.$ માં એક ઈલેક્ટ્રોનના પરિવર્તનથી $25°$ સે. એ$ 0.591\, V$ જોવા મળે છે. પ્રક્રિયા માટે સંતુલન અચળાંક કેટલો થાય?$ (F = 96500 C mol^{-1}; R = 8.314 JK^{-1} mol^{-1} )$View Solution
- 3ગ્લુકોઝનું કેલોરીફીક મૂલ્ય ......$KJ$View Solution
$C_6H_{12}O_6 + 6O_2 \rightarrow 6CO_2 + 6H_2O ; \Delta H = -2900 \,KJ/mole $
- 4ચુનાના પત્થરમાંથી ચુનાના રૂપાંતરણમાં,$CaCO_{3(s)} \rightarrow CaO_{(s)} + CO2_{(g)} 298 \,K$ અને $1$ બાર દબાણે $ \Delta H^°$ અને $ \Delta S^°$ ના મુલ્ય અનુક્રમે $+179.1\, kJ$ મોલ$^{-1}$ અને $160.2\, J/K$ છે. $ \Delta H^°$ અને $ \Delta S^°$ તાપમાન સાથે બદલાતા નથી. ઉપરના .....$K$ તાપમાને ચુનાના પત્થરથી ચુનાના રૂપાંતરણ સ્વયંભુ રીતે થશે ?View Solution
- 5ચોક્કસ પ્રક્રિયા માટે એન્થાલ્પી ફેરફાર અને એન્ટ્રોપી ફેરફાર અનુક્રમે $40.63\, kJ\, mol ^{-1}$ અને $100\, JK^{-1}$ છે.તો $27$ $^o$$C$ એ $\Delta G$ નું મૂલ્ય શું થશે ?View Solution
- 6જો $298 \,K$ એ $C-H, C-C, C-C$ અને $H-H$ બંધની બંધ ઉર્જા અનુક્રમે $414, 347, 615$ અને $435 \,kJ $ મોલ $^{-1}$ છે, તો પ્રક્રિયા માટે એન્થાલ્પી ફેરફારનું મૂલ્ય કેટલા .....$kJ$ થશે ? $H_2C = CH_{2(g)} + H_{2(g)} \rightarrow H_3C-CH_{3(g)}$ એ $298\, K$View Solution
- 7જો$A{l_2}{O_3}$ અને$C{r_2}{O_3}$ ની સર્જન-એન્થાલ્પી અનુક્રમે $- 1596\, kJ/mol$ અને $-1134\, kJ/mol$ હોય તો નીચેની પ્રક્રિયા માટે $\Delta H$ જણાવો .........$kJ$View Solution
$2Al + C{r_2}{O_3} \to A{l_2}{O_3} + 2Cr$
- 8જો $\Delta {H_{O - H}}$ નુ મૂલ્ય $109\, kcal\, mol^{-1}$ હોય, તો ${H_{\left( g \right)}}$ છે અને ${O_{\left( g \right)}}$ માંથી એક મોલ પાણીનુ સર્જન ............ સાથે સંકળાયેલ છે.View Solution
- 9જો $ Fe_2O_3$$_{(s)} + 3CO$ $_{(g)}$ $= 2Fe $$_{(s)} +$$3CO_2$$_{(g)}$ પ્રક્રિયાની પ્રમાણિત ઉષ્મા $ -6.6$ $kcal$ તો $Fe_2O_3$ $_{(s)}$ માટે $\Delta$$H_f$$^o$ $= ......$ $kcal/mol$ [ $\Delta$$H_f$$^o$ $CO$ $_{(g)} = -26.4\, kcal$ અને $\Delta$$H_f$$^o$ $CO_2$ $_{(g)}$$ = -94\, kcal $ ]View Solution
- 10જો $H_2, Cl_2 $અને $HCl$ માટે $S^o $ અનુક્રમે $0.13, 0.22$ અને $0.19 \,KJ \,K$$^{-1}$ મોલ$^{-1}$ છે. $H_2 + Cl_2 \rightarrow 2HCl$ પ્રક્રિયા માટે પ્રમાણિત એન્ટ્રોપીમાં થતુ કુલ ફેરફાર......$JK^{-1}\, mol^{-1}$View Solution
- 11જો $H_2$$_{(g)}$ $+$ $Cl_2$$_{(g)}$ $\rightarrow$ $2HCl$$_{(g)}$; $\Delta$ $H = -44 \,Kcal$; $2Na$$_{(s)}$ $+ 2HCl$$_{(g)}$ $\rightarrow$ $2NaCl$$_{(s)}$ $+$ $H_2$$_{(g)}$; $\Delta$$h =$ ${-1}52\, Kcal$ તો $Na$$_{(s)}$ $+ 0.5$ $Cl_2$$_{(g)}$ $\rightarrow$ $NaCl$$_{(s)}$ ; $\Delta H$ $= ?$ ......$Kcal$View Solution
- 12જો $S + O_2 \rightarrow \ SO_2 ; \Delta H = -298.2\, kJ; SO_2 + \frac{1}{2}\,O_2 \rightarrow SO_3 ; $View Solution
$\Delta H = - 98.7\,{\mkern 1mu} kJ{\mkern 1mu} {\mkern 1mu} S{O_3} + {H_2}O \to {H_2}S{O_4};\Delta H = - 130.2{\mkern 1mu} \,kJ;$
${H_2} + \frac{1}{2}{\mkern 1mu} {O_2} \to {H_2}O;{\Delta _H} = - 287.3{\mkern 1mu} \,kJ$
તો $298\, K$ એ $H_2SO_4$ ની નિર્માણ એન્થાલ્પી ............. $\mathrm{kJ}$ માં શોધો.
- 13જો $XY$, $X_2$ અને $Y_2$ ની બંધ તોડવા માટેની ઊર્જાનો ગુણોત્તર $1 : 1 : 0.5 $ અને $xy$ ની સર્જન ઉષ્મા $\Delta$$fH$ $+0.5a KJ/mol$ હોય તો $X_2$ ની બંધ તોડવા માટેની ઊર્જા .....$kJ\, mol^{-1}$ હશે.View Solution
- 14જો અચળ તાપમાન $T$ તથા દબાણ $P$ એ ઉષ્માશોષક પ્રક્રિયા આપમેળે થતી હોય તો આપેલા પૈકી સાચું કયું ?View Solution
- 15જો કોઇ રાસાયણિક પ્રક્રિયા માટે $\Delta H > 0$ અને $\Delta S > 0$ છે.તો કઇ પરિસ્થિતિમાં પ્રકિયા સ્વયંભૂ થશે નહિ ?View Solution
- 16જો કોઇ રાસાયણિક પ્રક્રિયા માટે $\Delta H = \Delta S > 0$ હોય, તો $\Delta H =$ ................View Solution
- 17જો પ્રક્રિયા માટે સંતુલન અચળાંક $10$ છે, તો $\Delta G$ નું મૂલ્ય ....... $(R = 8\,JK ^{-1} \,mol^{-1}, T = 300\,K)$View Solution
- 18જ્યારે $0\,^oC$ એ એક મોલ બરફનું પાણીમાં રૂપાંતર થાય તો એન્ટ્રોપી ફેરફાર શોધો ? ($J K$ $^{-1}$ મોલ$^{-1}$)માં ($0\,^oC$ એ બરફનું પ્રવાહીમાં થતું રૂપાંતરણ માટે એન્થાલ્પી ફેરફાર $6.0 \,KJ\,$ મોલ$^{-1}$ છે.)View Solution
- 19જ્યારે $0\,^oC$ તાપમાને અને $1\,atm$. જેટલા અચળ દબાણે $1$ મોલ બરફ પીગળે ત્યારે પ્રણાલી દ્વારા $1440\, cal$ ઉષ્માનુ શોષણ થાય છે. જો બરફ અને પાણીના મોલર કદ અનુક્રમે $0.0196\,L$ અને $0.0180\, L$ હોય તો પ્રણાલીની આંતરિક ઊર્જામાં થતો ફેરફાર.....$cal$ જણાવો.View Solution
- 20જ્યારે $3$ મોલ $Ar_{(g)}$ વાયુ અચળ દબાણે $229$ જૂલ ઉષ્મા આપવામાં આવે છે. તો નમૂનાનું તાપમાન $2.55$ કેલ્વિન વધે છે. વાયુની અચળ તાપમાને અને અચળ કદે મોલર ઉષ્મા ક્ષમતાની ગણતરી કરો.View Solution
- 21જ્યારે અચળ કદે $1$ મોલ વાયુને ગરમ કરતા તાપમાન વધીને $298 $ થી $308\, K$ થાય છે. જ્યારે વાયુને આપવી પડતી ઉષ્મા $500 \,J$ છે. ત્યારે કયું વિધાન સાચું હશે?View Solution
- 22View Solutionજ્યારે ડામર સખત ગરમ કરવામાં આવે તો.......
- 23View Solutionજ્યારે પ્રબળ બેઇઝના વધુ પ્રમાણ સાથે એસિડના એક તુલ્યાંક મિશ્ર કરવામાં આવે ત્યારે નીચેના પૈકી ક્યો એસિડ દ્રાવણના તાપમાનમાં મહત્તમ વધારો દર્શાવશે ?
- 24View Solutionજ્યારે વાયુ સમોષ્મી અને પ્રતિવર્તીં રીતે સંકોચાય ત્યારે અંતિમ તાપમાન.......
- 25View Solutionજ્યારે હિલિયમ વાયુનુ શૂન્યાવકાશમાં વિતરણ કરવામાં આવે ત્યારે heating effect જોવા મળે છે. તેનું કારણ શું છે ?
- 26View Solutionદ્રીપરમાણ્વીય વાયુ માટે અચળ દબાણે અને અયળ કદે વિશિષ્ટ ઉષ્માનો ગુણોત્તર ........... થશે.
- 27નાઈટ્રોજનના પરિમાપન માટે લીધેલા $0.3 $ ગ્રામ કાર્બનિક સંયોજનમાંથી ઉદભવતા એમોનિયાને $100 \,mL$ $ 0.1$ $M\, H_2SO_4$ માંથી પસાર કરવામાં આવે છે. વધારાનું એસિડનું સંપૂર્ણ તટસ્થીકરણ કરવા માટે $ 20\, mL\, 0.5 $ $M\, NaOH$ ની જરૂર પડે છે. આકાર્બનિક પદાર્થ કયો હશે ?View Solution
- 28નીચે આપેલા $298\, K $ અને $1$ વાતા આપેલ એન્ટ્રોપીના મુલ્ય $H_2$$_{(g)}$ : $130.6$, $Cl_2 $$_{(g)}$ : $223.0$ અને $HCl_{(g)}$ : $186.7$ છે તો પ્રક્રિયા માટે એન્ટ્રોપી ફેરફાર $(JK^{-1}$ મોલ$^{-1}$)માં ..... થશે.$H_2$$_{(g)}$ $+$ $Cl_2$ $_{(g)}$ $\rightarrow$ $2HCl$$_{(g)}$View Solution
- 29નીચેના કયા એક સમીકરણ માટે $\Delta H^o$ પ્રક્રિયાએ નિપજના $\Delta H_f$ બરાબર હોય છે ?View Solution
- 30નીચેના પૈકી કઇ પ્રક્રિયા પ્રતિમોલ $57.3\, kJ$ ઉષ્મા મુકત કરે છે ?View Solution
- 31View Solutionનીચેના પૈકી કઇ પ્રક્રિયામાં એન્ટ્રોપી વધે છે ?
- 32View Solutionનીચેના પૈકી કોણ સૌથી વધારે એન્ટ્રોપી પર મોલ ધરાવે છે ?
- 33નીચેના પૈકી ક્યા પ્રકમ માટે $\Delta {H^o} - \Delta {G^o}$ મૂલ્ય લગભગ શૂન્ય થશે ?View Solution
- 34નીચેના પૈકી ક્યા પ્રકમ સાથે એન્ટ્રોપીનો વધારો સંકળાયેલ છે ?View Solution
$(I)$ ધનનુ ગલન $(II)$ વાયુઓને મિશ્ર ક્રરવા
$(III)$ વાયુનુ સંકોચન $(IV)$ વાયુનુ વિસ્તરણ
- 35View Solutionનીચેના પૈકી ક્યુ વિધાન સાચું છે ?
- 36View Solutionનીચેના પૈકી ક્યુ વિધાન સાયુ છે ?
- 37View Solutionનીચેના પૈકી ક્યુ સાચું છે ?
- 38View Solutionનીચેના પૈકી ક્યુ સાચું છે ?
- 39નીચેના પ્રકમ માટે $\Delta H$ નુ મૂલ્ય કેવું હશેView Solution
${X_{\left( g \right)}} + {e^ - } \to X_{\left( g \right)}^ - $
- 40નીચેના પ્રક્રિયા ધરાવતા પ્રમાણિત વિધૂતરાસાયણિક કોષનો પોટૅન્શિયલ $1.20$ વોલ્ટ હોય, તો પ્રક્રિયા સાથે સંકળાયેલ મુક્ત-ઊર્જા ફેરફારનું મૂલ્ય કિલો જૂલમાં ગણો.View Solution
$2Ag_{(aq)}^ + + c{d_{(s)}} \to cd_{(aq)}^{2 + } + 2A{g_{(s)}}$
- 41View Solutionનીચેનામાંથી આપમેળે થતી પ્રક્રિયા શું કરશે ?
- 42નીચેનામાંથી કઇ પ્રક્રિયા માટે $\Delta H$ નુ મૂલ્ય ધન હશે ?View Solution
- 43નીચેનામાંથી કઈ એક કે જેનો $\Delta S$ શુન્ય કરતા વધારે હોય છે ?View Solution
- 44View Solutionનીચેનામાંથી કઈ જોડ રાસાયણિક પ્રક્રિયાના સ્વયંભૂ પ્રક્રિયામાં પરિણામે નિશ્ચિત છે ?
- 45View Solutionનીચેનામાંથી કયાં માત્રાત્મક ગુણધર્મ છે ?
- 46View Solutionનીચેનામાંથી કયું ઉષ્માગતિશાસ્ત્ર પ્રાણાલીનો અવસ્થા વિધેય નથી ?
- 47નીચેનામાંથી કયું સમીકરણ $CH_4$ ની પ્રમાણીત નિર્માણ ઉષ્મા દર્શાવે છે ?View Solution
- 48નીચેનામાંથી ક્યુ ${\left[ {\partial P/\partial V} \right]_T}$ ને સમાન થશે ?View Solution
- 49View Solutionનીચેનામાંથી ક્યુ વિધાન સાચું છે ?
- 50View Solutionનીચેનામાંથી ક્યુ વિધાન સાચું છે ?
- 51View Solutionનીચેનામાંથી ખોટું સમીકરણ કયું છે ?
- 52નીચેનામાંથી નિર્માણ ઉષ્માનું .....$K\, cal$ મુલ્ય દર્શાવે છે કે નિપજ ઓછું સ્થાયી છે ?View Solution
- 53નીચેનામાંથી શાના માટે $q = \Delta U$ થશે ?View Solution
- 54નીચેના સમીકરણ દ્વારા મિથેનના દહનમાં ઉદભવતી ઉષ્માનું મૂલ્ય આપેલ છે. જો $445 kJ$ દહન ઉષ્મા ઉત્પન્ન કરવા માટે કેટલા ...... ગ્રામ મિથેનની જરૂર પડે છે ?View Solution
$CH _{4}+2 O _{2} \rightarrow CO _{2}+2 H _{2} O (\Delta H =-891 kJ / mol)$
- 55નીચેના સમીકરણ દ્વારા મિથેનના દહનમાં ઉદ્રભવતી ઉષ્માનું મૂલ્ય આપેલ છે. જ્યારે $445\, kJ$ ઉષ્મા ઉદ્રભવે ત્યારે કેટલા..... ગ્રામ કાર્બન ડાયોકસાઈડ મળે છે ?View Solution
- 56નીચેની કઈ પ્રક્રિયા માટે $\Delta S $ મહતમ થશે ?View Solution
- 57નીચેની માહિતી પરથી $KCl$ ની મંદન એન્થાલ્પી ............$kJ$ થશેView Solution
$KC{l_{\left( s \right)}} + 20{H_2}O \to KCl\,\left( {20\,{H_2}O} \right);\Delta H = + 15.90\,kJ$
$KC{l_{\left( s \right)}} + 200{H_2}O \to KCl\,\left( {200\,{H_2}O} \right);\Delta H = + 18.58\,kJ$
- 58નીચેની માહિતી પરથી ઇથિલિનની સર્જન એન્થાલ્પી.......$kJ\,mo{l^{ - 1}}$ ગણો.View Solution
${C_{\left( {graphite} \right)}} + {O_{2\left( g \right)}} \to C{O_{2\left( g \right)}}\,;\Delta H = - 393.5\,kJ$
${H_{2\left( g \right)}} + 1/2{O_{2\left( g \right)}} \to {H_2}{O_{\left( l \right)}}\,;\,\Delta H = - 286.2\,kJ$
${C_2}{H_{4\left( g \right)}} + 3{O_{2\left( g \right)}} \to 2C{O_{2\left( g \right)}} + 2{H_2}{O_{\left( l \right)}}\,;\,\Delta H = - 1410.8\,kJ$
- 59નીચેની માહિતી પરથી નાઇટ્રિક ઓક્સાઇડની સર્જન એન્થાલ્પી કેટલા .......$kJ\,mo{l^{ - 1}}$ થશે ?$N{O_{\left( g \right)}} + C{O_{\left( g \right)}} \to 1/2{N_{2\left( g \right)}} + C{O_{2\left( g \right)}};\Delta {H^o} = - 372.2\,kJ/mol$View Solution
$\Delta H_f^o\left( {CO} \right) = - 110.5\,kJ\,mo{l^{ - 1}};$
$\Delta H_f^o\left( {C{O_2}} \right) = - 393.5\,kJ\,mo{l^{ - 1}}$
- 60નીચેની માહિતી પરથી પ્રક્રિયામાં થતો ઉષ્મા ફેરફાર કરો. $NH_3$ $_{(g)}$ + $HCl$$_{(g)}$ $\rightarrow$ $NH_4Cl$$_{(s)}$View Solution
$(i)$ $NH_3$ $_{(g)} + aq$ $\rightarrow$ $NH_3$ $_{(aq)}$, $\Delta H$ $= -8.4 \,Kcal.$
$(ii)$ $HCl_{(g)} + aq$ $\rightarrow$ $HCl{(aq)}$, $\Delta H =$ ${-1}7.3\, Kcal.$
$(iii)$ $NH_3$ $_{(aq)} + HCl_{(aq)}$ $\rightarrow$ $NH_4Cl $ $_{(aq)}$, $\Delta H = -12.5\, Kcal$.
$(iv)$ $NH_4Cl$ $_{(s)} + aq$ $\rightarrow$ $NH_4Cl$ $_{(aq)}$, $\Delta H = +3.9 \,Kcal.$
- 61નીચેની માહિતી પરથી પ્રવાહી પાણીના બાષ્પીભવન એન્થાલ્પી .....$KJ \,mol^{-1}$ થશે :View Solution
$H_2$$_{(g)} +$ $1/2O_2$ $_{(g)}$ $\rightarrow$ $H_2$$O$$_{(l)}$; $\Delta H= -$ $285.77\, KJ\, mol$$^{-1}$; $H_2$$_{(g)} +$ $1/2O_2$$_{(g)}$ $\rightarrow$ $H_2O$ $_{(g)}$; $\Delta H$ $ = - 241.84\, KJ \,mol$$^{-1}$
- 62નીચેની માહિતી પરથી સુક્રોઝના $ (C_{12}H_{22}O_{11})$ નિર્માણ એન્થાલ્પીની ગણતરી ............. $\mathrm{JK}^{-1} \, \mathrm{mol}^{-1}$ થશે.View Solution
$(i)\,\,{C_{12}}{H_{22}}{O_{11}}\,\, + \,\,12{O_2}\,\, \to \,\,12\,\,C{O_2}\, + \,\,11{H_2}O,\,\,\,\,\,\,\,\,\,\,\,\,\Delta H\,\, = \,\, - 5200.7\,kJ\,mo{l^{ - 1}} $
$(ii)\,\,C\,\, + \,\,{O_2}\, \to \,\,C{O_2},\,\,\,\,\,\,\,\,\,\,\,\,\Delta H\,\, = \,\, - \,394.5\,\,kJ\,\,mo{l^{ - 1}}$
$(iii)\,\,{H_2}\,\, + \,\frac{1}{2}{O_2}\,\, \to \,\,\,{H_2}O,\,\,\,\,\,\,\,\,\,\Delta H\,\, = \,\, - \,285.8\,kJ\,\,mo{l^{ - 1}}$
- 63નીચેની માહિતીમાંથી $1.8\,^oC$ એ $Ca(OH)_2$$_{(s)}$ ની નિર્માણ ઉષ્મા ......$K\,cal.$View Solution
$CaO_{(s)}\,\, + \,\,{H_2}O_{(l)}\,\, \to \,\,Ca{(OH)_2}_{(s)}\,;\,\,\,........(i)$ $\,\Delta {H_{1.8\,^oC}} = \,\, - \,\,15.26\,\,K\,cal$
$H_2O_{(l)}\,$ $ \to $ ${H_{2{(g)}}}$ $+$ $\frac{1}{2}O_{2(g)}$ $\,\Delta {H_{1.8\,^oC}} = \,\, - \,\,68.37\,\,K\,cal$
$Ca_{(s)} + \frac{1}{2}O_{2(g)} = CaO_{(s)}$ $\,\Delta {H_{1.8\,^oC}} = \,\, \,\,-151.80\,\,K\,cal$
- 64પાણીના ઉત્કલન બિંદુએ $900\,J/g$ ઉષ્માનો વિનિમય થાય છે. તો એન્ટ્રોપીમાં થતો વધારો કેટલા ......$J/K-mole$ ?View Solution
- 65પાણીના બાષ્પાયન માટે $1$ વાતા દબાણે પ્રવાહી પાણી અને પાણીની બાષ્પમાં સંતુલન હોય ત્યારે તાપમાનનું મૂલ્ય કેટલા....$K$ થશે ?View Solution
$H_2O$ $_{(l)}$ $\rightleftharpoons$ $H_2O$ $_{(g)}$ [$1$ વાતા દબાણે] $[ \Delta S = 120 \,JK^{-1}$ અને $\Delta H = +45.0\, KJ ]$
- 66પાણીની બાષ્પ આદર્શ વાયુ છે. જ્યારે $1$ બાર દબાણ અને $100\,^{o}C$, એ $1$ મોલ પાણીનું બાષ્પીભવન થાય તો આંતરિક ઉર્જા ફેરફાર ($\Delta U$) શોધો. ($1$ બાર અને $373\,K$ પાણીની મોલર બાષ્પાયન એન્થાલ્પી $= 41\, kJ$ મોલ$^{-1}$ અને $R = 8.3 \,J$ મોલ$^{-1}$ $K$$^{-1}$)View Solution
- 67પાણીમાં $NaO{H_{\left( s \right)}}$ ની દ્રાવણ ઉષ્મા $ - 41.6\,kJ\,mo{l^{ - 1}}$ છે. જ્યારે $NaO{H_{\left( s \right)}}$ ને પાણીમાં દ્રાવ્ય કરવામાં આવે ત્યારે પાણીનું તાપમાન ..........View Solution
- 68પાણીમાં એક મોલ નિર્જળ $AB$ ક્ષારને દ્રાવ્ય કરતાં $21.0 \,J\, mol ^{-1}$ ઉષ્મા છૂટી પડે છે. $AB$ ના $\Delta H$ હાઈડ્રેશનનું મૂલ્ય $-29.4\, J\, mol ^{-1}$ છે. તો $AB.2H_2O$ $_{(s)}$ ક્ષારની હાઈડ્રેટેડ દ્રાવ્યની ઉષ્મા કેટલા .....$J\, mol ^{-1}$ ?View Solution
- 69View Solutionપુરોગામી પ્રક્રિયા આપમેળે થાય તે માટે જરૂરી શરત ...... છે.
- 70પ્રકિયા $2{C_{\left( {graphite} \right)}} + 2{H_{2\left( g \right)}} \to {C_2}{H_{4\left( g \right)}}$ માટે એન્થાલ્પી ફેરફાર......$kJ$ ગણો.View Solution
${C_{\left( {graphite} \right)}} + {O_{2\left( g \right)}} \to C{O_{2\left( g \right)}}\,;\,\Delta H = -393.5\,kJ$
${C_2}{H_{4\left( g \right)}} + 3{O_{2\left( g \right)}} \to 2C{O_{2\left( g \right)}} + 2{H_2}{O_{\left( l \right)}}\,;\,\Delta H = - 1410.9\,kJ$
${H_{2\left( g \right)}} + 1/2{O_{2\left( g \right)}} \to {H_2}{O_{\left( l \right)}}\,;\,\Delta H = - 285.8\,kJ$
- 71પ્રક્રિયા $2{H_{2\left( g \right)}} + {O_{2\left( g \right)}} \to 2{H_2}{O_{\left( l \right)}}$ માટે $\Delta H = - 571\,kJ$ છે. જો $H - H$ બંધઊર્જા $435\,kJ\,mo{l^{ - 1}}$ અને $O = O$ બંધઊર્જા $498\,kJ\,mo{l^{ - 1}}$ હોય, તો $O - H$ બંધની સરેરાશ ઊર્જા.....$kJ\,mo{l^{ - 1}}$ ગણો.View Solution
- 72પ્રક્રિયા $A \to B$ માટે $\Delta H = 4\,kcal\,mo{l^{ - 1}}$ અને $\Delta S = 10\,cal\,{K^{ - 1}}\,mo{l^{ - 1}}$ હોય, તો પ્રક્યિા .......$K$ તાપમાને સ્વયંભૂ હોઇ શકે ?View Solution
- 73પ્રક્રિયા $Cu_{\left( g \right)}^ + + I_{\left( g \right)}^ - \to Cu{I_{\left( s \right)}}$ માટે $\Delta {H^o}$ નું મૂલ્ય $ - 446\,kJ\,mo{l^{ - 1}}$ છે. જો $C{u_{\left( g \right)}}$ ની આયનીકરણ ઊર્જા $ 745\,kJ\,mo{l^{ - 1}}$ હોય અને ${I_{\left( g \right)}}$ ની ઇલેક્ટ્રોન બંધુતા $ -295\,kJ\,mo{l^{ - 1}}$ હોય, તો $C{u_{\left( g \right)}}$ અને ${I_{\left( g \right)}}$ માંથી $Cu{I_{\left( s \right)}}$ ના સર્જન માટે $\Delta {H^o}$ નુ મૂલ્ય.......$kJ$ જણાવો.View Solution
- 74પ્રક્રિયા $(i) \,{H_2}_(g)\,\, + \,\,C{l_2}(g)\,\, \to \,\,2HCl(g)\,\, + \,\,x\,KJ\,\,\,\,$View Solution
$(ii)\,{H_2}(g)\,\, + \,\,C{l_2}(g)\,\, \to \,\,2HCl(\ell )\,\, + \,\,y\,KJ$ માટે નીચેનામાંથી કયુ વિધાન સાચુ છે ?
- 75View Solutionપ્રક્રિયા આપમેળે થતી ન હોય, તો ...... વિકલ્પ સાચો છે.
- 76પ્રક્રિયાની ઉષ્મા નીચે પ્રમાણે છે : તો પ્રક્રિયા $C_2H_2$ + $H_2$ $\rightarrow$ $C_2H_4$ માટે ઉષ્મા ફેરફાર......$ K\, cal$View Solution
$(i)\,\,\Delta H_f^o\,\,of\,{H_2}{O_{(\ell )}}\, = \,\, - 68.3\,K\,\,cal\,\,mo{l^{ - 1}}$
$(ii)\,\,\Delta H_{comb}^o\,\,of\,{C_2}{H_2}\, = \,\, - 337.2\,K\,\,cal\,\,mo{l^{ - 1}}$
$(iii)\,\,\Delta H_{comb}^o\,\,of\,\,{C_2}{H_4}\,\, = \,\, - \,363.7\,\,K\,\,cal\,\,mo{l^{ - 1}} $
- 77પ્રક્રિયાની એન્થાલ્પીનો ઉપયોગ કરી $H_2O_2$$_{(l)}$ ના નિર્માણની એન્થાલ્પી......$kJ/mol$ માં શોધો.View Solution
$(i)$ $N_2H_4$$_{(l)}$ $+$ $2H_2O_2$$_{(l)}$ $\rightarrow$ $N_2$$_{(g)}$ $+$ $4H_2O$$_{(l)}$; $\Delta r{H_1}^ \circ = - 818 \,kJ/mol$
$(ii)$ $N_2H_4$$_{(l)}$ $+$ $O_2$$_{(g)}$ $\rightarrow$ $N_2$$_{(g)}$ $+$ $2H_2O$$_{(l)}$; $\Delta r{H_2}^ \circ = - 622 \,kJ/mol$
$(iii)$ ${H_2}_{(g)}\,\, $+$ \,\,\frac{1}{2}\,{O_2}_{(g)}\,\, \to \,\,{H_2}O_{(l)}\,\,\,;\,\,{\Delta }r{H_3}^ \circ \, = \,\, - 285\,\,kJ/mol$
- 78પ્રક્રિયામાં એન્થાલ્પી ફેરફાર ....... તરીકે ઓળખાય છે.View Solution
$2CO_{(g)} + O_{2{(g)}}$ $\rightarrow$ $2CO_{2{(g)}}$
- 79પ્રક્રિયા માટેનું $\Delta H^o\,\, -352.8\, kJ$ છે તો $F_2 + 2HCl$ $\rightarrow$ $2HF + Cl_2$ જો $HF$ માટે $\Delta H_f^o\,\, -268.3 \,kJ$ મોલ$^{-1}$ હોય તો $HCl$ ની $\Delta H_f^o$........$kJ$ મોલ$^{-1}$ થશે.View Solution
- 80પ્રતિમોલ ઈથેનોલની બાષ્પાયન એન્થાલ્પી કેટલા ............ $\mathrm{kJ/mol}$ થશે ? $(b.p. = 79.5\,^oC$ અને $\Delta S$ $= 109.8 $ $JK^{-1}\, mol^{-1}$) છે.View Solution
- 81પ્રતિવર્તીં પ્રક્રિયા માટે $T = 300\,K,$ કદ વધીને $V_f = 1\,L$ થી$ V_f = 10\,L$ થાય છે. તો જો પ્રક્રિયા સમઉષ્મીય હોય તો $\Delta H$ ................. $\mathrm{kJ}$ શોધો.View Solution
- 82પ્રબળ એસિડ અને પ્રબળ બેઈઝના તટસ્થીકરણથી પ્રતિ મોલ $H^+$ આયનોએ ઉદભવતી ઉષ્મા એ ...... હોય છે.View Solution
- 83View Solutionપ્રમાણિત મુક્ત ઊર્જા ફેરફાર અને સંતુલન અચળાંક વચ્ચેનો યોગ્ય સંબંધ ...... છે.
- 84View Solutionપ્રવાહીનું બાષ્પીભવન માટેની પ્રક્રિયા ....... થઈ પૂર્ણ થાય છે.
- 85પ્રાણાલી દ્વારા થતું કાર્ય $8\,J$ છે. જ્યારે $40\,J$ ઉષ્મા પસાર કરવામાં આવે ત્યારે પ્રક્રિયા દરમ્યાન પ્રાણાલીની આંતરિક ઉર્જામાં થતો ફેરફાર......$J$View Solution
- 86પ્રાણાલીની આંતરિક ઉર્જા $U_1$ છે, તો બહારથી $450\, J$ ઉષ્મા લે છે અને $600\, J$ કાર્ય પુરૂ કરે છે તો પ્રાણાલીની અંતિમ ઉર્જા .......View Solution
- 87બંધ પાત્રમાં $2$ મોલ કાર્બન મોનોકસાઈડ અને એક મોલ ઓક્સિજનનું મિશ્રણ પ્રજવલિત થઈને કાર્બન ડાયોકસાઈડ મળે છે. જો $\Delta H$ એન્થાલ્પી ફેરફાર અને $\Delta U$ એ આંતરિક ઉર્જામાં ફેરફાર થાય તો.....View Solution
- 88બે ઈલેકટ્રોનના ફેરફારને સમાવતી કોષ -પ્રક્રિયાનો પ્રમાણિત કોષ પોટેન્શિયલ $25^{0} C$ તાપમાને $0.295V$ છે. તો તેનો $25°C$ તાપમાને સંતુલન અચળાંક કેટલો થાય?View Solution
- 89બેન્ઝિનની દહન પ્રક્રિયા દરમિયાન થતો એન્થાલ્પી ફેરફાર$ = -3264.6$ કિલોજૂલ/મોલ હોય, તો $39$ ગ્રામ બેન્ઝિનના દહનથી ઉદભવતી ઉષ્મા ...... કિલોજૂલ હોય.View Solution
- 90બોમ્બ કેલેરીમીટરમાં એક મોલ ઝીંક રજ સાથે એક મોલ સલ્ફયુરીક એસિડની ઉષ્માક્ષેપક પ્રક્રિયા માટે $\Delta U$ અને $w$ નો સંબંધ .....View Solution
- 91મંદ $NaOH$ દ્રાવણ દ્વારા $1\,M\, HCl$ અને $1\, M\, H_2SO_4$ નાં સમાન કદનું તટસ્થીકરણ થાય છે અને $x$ અને $y \,K $ કેલરી ઉષ્મા અનુક્રમે છૂટી પડે છે. નીચેનામાંથી કયુ સાચું છે ?View Solution
- 92મિથેનના દહનનું $\Delta U^{\theta}$ મૂલ્ય $-X \,kJ \,mol ^{-1}$ છે. $\Delta H^{\theta}$ નું મૂલ્ય શું હશે ?View Solution
- 93મિથેનની દહનઉષ્મા $- 809\, kJ\, mol^{-1}$ છે. તો મિથેનનુ કેલરીમૂલ્ય કેટલા ....$kJ\,mo{l^{ - 1}}$ થશે ?View Solution
- 94રહોમ્બિક અને મોનોક્લિનિક સલ્ફરની દહન એન્થાલ્પી અનુક્રમે $70,960 $ અને $71,030$ કેલરી છે, તો રહોમ્બિક સલ્ફરના મોનોક્લિનિક સલ્ફરમાં થતાં રૂપાંતરણની એન્થાલ્પી ...... કેલરી થાય.View Solution
- 95વાયુમય પ્રક્રિયા માટે $A_{(g)} + 3B_{(g)} \rightarrow 3C_{(g)} + 3D_{(g)}$ $27\,^oC$ એ $\Delta U=17 \,Kcal$ છે. ધારો કે $R = 2 \,cal \,K$$^{-1}$ મોલ$^{-1}$ છે તો ઉપરની પ્રક્રિયા માટે $\Delta H$ નું મુલ્ય .......$Kcal$ થશે.View Solution
- 96View Solutionવિધાન : સંતુલને દરેક રાસાયણિક પ્રક્રિયા માટેનો પ્રક્રિયાનો પ્રમાણિત ગીબ્સ ઉર્જા ફેરફાર શૂન્ય થાય છે.
કારણ : અચળ તાપમાન અને દબાણે રાસાયણિક પ્રક્રિયા ગીબ્સ ઉર્જાના ઘટાડાની દિશામાં સ્વયંભુ થાય છે.
- 97વ્યક્તિ રોજ $640\,g \,\,O_2$ શ્વાસમાં લે છે. જો બધો જ $O_2$ શર્કરાનું $CO_2$ અને $H_2O$ માં રૂપાંતર માટે વપરાતો હોય તો કેટલો સુક્રોઝ ($C_{12}H_{22}O_{11}$) એક દિવસમાં શરીરમાં વપરાશે અને કેટલા .....$kJ$ ઉષ્મા ઉત્પન્ન] થાય છે ? $\Delta _{Hcombustion\, of\, sucrose}= -5645\, kJ\, mol^{-1}$.View Solution
- 98સમાન કદ ધરાવતા મોલર હાઇડ્રોક્લોરિક એસિડ અને સલ્ફયુરિક એસિડનું તટસ્થીકરણ મંદ $NaOH $ ના દ્રાવણ વડે કરતાં અનુક્રમે $x$ $KCal$ અને $y$ $KCal$ ઉષ્મા ઉત્પન્ન થાય છે. તો નીચેના પૈકી કયું સાચું છે ?View Solution
- 99સમીકરણના આધારે $1 $ લીટર કદના પાત્રમાં $2$ મોલ $CO$ અને $1$ મોલ $O_2$ લેવામાં આવે છે. જે નીચેના સમીકરણ દ્વારા $2$ મોલ $CO_2$ બનાવે છે.View Solution
$2CO + O_2 \rightarrow 2CO_2, \Delta H = - 560\,KJ.$ (આદર્શ સ્વરૂપમાંથી વાયુનું વિચલન થાય છે.$1\, atm - litre = 0.1\, KJ$)આ પ્રક્રિયા માટે, દબાણમાં $70\, atm $ થી $40\, atm$ ફેરફાર થાય છે. તો $500\, K$ એ $\Delta$$U$ નું મૂલ્ય ......$KJ$ શોધો.
- 100સમીકરણોની મદદથી $x$ ની $\to$ કિંમત......કિલોજૂલ માં શોધો :View Solution
${H_2}{O_{(g)}} + {C_{(s)}}\, \to \,\,C{O_{(g)}} + {H_{2(g)}}\,:\,\,\Delta H\, = \,\,131$ કિલોજૂલ $C{O_{(g)}} + \,\,\frac{1}{2}\,\,{O_{2(g)}} \to \,\,C{O_{2(g)}}\,:\,\,\Delta H\,\, = \,\, - 282$ કિલોજૂલ
${H_{2(g)}} + \frac{1}{2}{O_{2(g)}} \to \,{H_2}{O_{(g)}}\,:\,\Delta H\,\, = \,\, - 242\,\,$ કિલોજૂલ
$C_{(g)} + O_2$$_{(g)}$ $\to$ $CO_2$$_{(g)}$ : $\Delta H = x$ કિલોજૂલ