Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1a मीटर भुजा वाले वर्ग के चारों कोनों पर क्रमशः q, 2q , 3q व 4q फूलॉम आवेश स्थित हैं। सिद्ध कीजिए कि उसके केन्द्र पर विद्युत क्षेत्र $4 \sqrt{2} \frac{k q}{a^2}$ न्यूटन/कूलॉम होगा।View Solution
- 2View Solutionदो आवेश वायु में कुछ दूरी पर रख दिये गये हैं-
(अ) यदि उनके बीच एक काँच की स्लेब जिसका परावैद्युतांक 8 है रख दी जाये तो उनके बीच कार्य करने वाले बल के परिमाण में क्या परिवर्तन होगा?
(ब) यदि पीतल का टुकड़ा रख दिया जाये तो क्या होगा? - 3समान आवेश वाले दो धनायन एक$-$दूसरे को $3.7 \times 10^{-9}$ न्यूटन बल से प्रतिकर्षित करते हैं जबकि उनके बीच की दूरी $5 \mathring A$ है। प्रत्येक आयन में सामान्य अवस्था की तुलना में कितने इलेक्ट्रॉन कम हैं?View Solution
- 4$(अ) \ 12.5 \times 10^8$ इलेक्ट्रॉन पर कितना आवेश होगा?View Solution
$(ब) \ 1$ कूलॉम आवेश तथा $1$ इलेक्ट्रॉन आवेश में कौन बड़ा है? $1$ कूलॉम आवेश में कितने इलेक्ट्रॉनिक आवेश होंगे? - 5View Solutionदो बिन्दु आवेश 5 µC तथा- 5 µC एक-दूसरे से 1 सेमी. की दूरी पर रखे हैं। इनके मध्य बिन्दु से 0.30 मीटर की दूरी पर (i) अक्षीय स्थिति में, (ii) निरक्षीय स्थिति में वैद्युत क्षेत्र की तीव्रता की गणना कीजिए।
- 6View Solutionसमान प्रकृति के दो q आवेश परस्पर d दूरी पर स्थित हैं, इनको मिलाने वाली रेखा के मध्य बिन्दु पर तीसरा आवेश Q कूलॉम का रखा है। Q के किस मान के लिए निकाय संतुलन में होगा?
- 7दो विद्युतरोधी आवेशित ताँबे के गोले '$A$' एवं '$B\ $' जो आकार में सर्वसम हैं, के केन्द्रों के बीच की दूरी $50$ सेमी. तथा दोनों पर पृथक$-$पृथक आवेश $6.5\times 10^{-7} C$ है। इसी आकार का एक तीसरा अनावेशित गोला '$C\ $' सर्वप्रथम पहले गोले '$A$' के सम्पर्क में तत्पश्चात् दूसरे गोले '$B\ $' के सम्पर्क में लाकर अन्ततः दोनों से ही हटा लिया जाता है, तब '$A$' व '$B\ $' गोलो के मध्य लगने वाले प्रतिकर्षण बल का मान ज्ञात करो।View Solution
- 8View Solutionधातु के एक पतले खोखले गोले (गोलीय कोश) की त्रिज्या 30 सेमी. तथा उस गोलीय कोश पर 500 µC का आवेश है। कोश के केन्द्र से (i) 1 मीटर की दूरी पर, (ii) 30 सेमी. दूरी पर, (iii) 10 सेमी. दूरी पर विधुत क्षेत्र की तीव्रता ज्ञात कीजिए।
- 91 µC के अनन्त आवेश x अक्ष पर x = 1, 2, 4,8,…. $\infty$ स्थितियों पर रखे हैं। यदि 1C का आवेश मूल बिन्दु पर 8, स्थित है तो इस पर आरोपित कुल बल का मान बताइए।View Solution
- 10View Solutionदो परमाणुओं को आयन बनाने के लिए उनमें प्रत्येक से 2 इलेक्ट्रॉन निकाले गये हैं। इन आयनों को निर्वात में रखने पर ये एक-दूसरे को 3.7 × 10-9 न्यूटन बल से प्रतिकर्षित करते हैं। उनके बीच की दूरी ज्ञात कीजिए।
- 11समरूप विद्युत क्षेत्र $1.6 \times 10^5 \ V/m$ में स्थित $a$ कण का द्रव्यमान $6.4 \times 10^{-27}\ Kg$ है तथा आवेश $3.2 \times 10^{-19} C$ है। विराम स्थिति में $2 \times 10^{-2}m$ का पथ तय करने के बाद कण का वेग क्या होगा ?View Solution
- 12एक $10$ सेमी. व्यास के गोले को आवेशित किया जाता है जिससे इसके पृष्ठ पर विद्युत क्षेत्र की तीव्रता $5 \times 10^6$ वोल्ट प्रति मीटर हो जाती है। गोले के केन्द्र से $25$ सेमी. दूरी पर स्थित $5 \times 10^{-2}$ माइक्रो कूलॉम आवेश पर कितना बल लगेगा?View Solution
- 13एक $17.7 \times 10^{-4}$ कूलॉम का वैद्युत आवेश $200$ मीटर क्षेत्रफल की बड़ी पतली चादर पर समान रूप से फैला हुआ है। इससे $20$ सेमी. की दूरी पर वायु में वैद्युत क्षेत्र की तीव्रता ज्ञात कीजिए।View Solution
- 14त्रिज्या r तथा लम्बाई l के एक बेलनाकार पृष्ठ में आवेश घनत्व $\lambda$तथा अनन्त लम्बाई का पतला, सीधा चालक तार परिबद्ध है। बेलनाकार पृष्ठ की अक्ष तार की लम्बाई से संपाती है।बेलनाकार पृष्ठ से विद्युत फ्लक्स के लिए व्यंजक ज्ञात कीजिए।View Solution
- 15. L मीटर भुजा का वर्गाकार पृष्ठ कागज के तल में रखा हुआ है। एक समानविधुत क्षेत्र $\overrightarrow{ E }$ भी कागज के तल में ही है तथा यह चित्रानुसार, पृष्ठ के निचले आधे भाग तक ही सीमित है। तल से बद्ध वैद्युत फ्लक्स कितना होगा?View Solution

- 16View Solutionएकसमान विद्युत क्षेत्र में विद्युत बल रेखाओं की प्रकृति क्या है?
- 17View Solutionविधुत द्विध्रुव तथा द्विध्रुव आघूर्ण को परिभाषित करते हुए द्विध्रुव की निरक्ष (विषुवतीय तल) पर स्थित किसी बिन्दु पर क्षेत्र की तीव्रता के लिए आवश्यक सूत्र ज्ञात कीजिए।
- 18View Solutionविधुत द्विध्रुव के कारण विषुवतीय तल पर स्थित किसी बिन्दु पर विधुत क्षेत्र का सूत्र व्युत्पन्न कीजिए। आवश्यक चित्र बनाइए।
- 19View Solutionस्थिर वैद्युतिकी के लिए गाउस नियम का कथन लिखिए। चित्र बनाकर एक समान आवेशित अनन्त समतल चादर के कारण इसके नजदीक किसी बिन्दु पर विधुत क्षेत्र के लिए व्यंजक व्युत्पन्न कीजिए।
- 20सिद्ध कीजिए कि अनन्त विस्तार की आवेशित परत के कारण उसके निकट किसी बिन्दु पर विधुत क्षेत्र का मान पृष्ठ के क्षेत्रफल तथा परत से दूरी पर निर्भर नहीं करता है। अर्थात् परत के निकट बिन्दुओं पर विधुत क्षेत्र एकसमान रहता है।###गाउस का नियम लिखिए। इस नियम के अनुप्रयोग से एकसमान आवेशित अनन्त समतल चादर के कारण चादर के समीप स्थित किसी बिन्दु पर विद्युत क्षेत्र का मान ज्ञात कीजिए। ###गाउस नियम का उपयोग करके यह दर्शाइए कि किसी एकसमान आवेशित अनन्त समतल चादर के कारण किसी बिन्दु पर विद्युत क्षेत्र$\overrightarrow{ E }=\frac{\sigma}{2 \epsilon_0} \hat{ n }$में से व्यक्त होता है। यहाँ प्रतीकों के अपने सामान्य अर्थ हैं।View Solution
- 21(ii) 12 सेमी. त्रिज्या वाले गोलीय चालक के पृष्ठ पर $1.6 \times 10^{-7}$ Cआवेष एक समान रूप से वितरित है। गोले के अन्दर गोले के ठीक बाहर गोले के केन्द्र से 18 सेमी दूरी पर स्थित बिन्दु पर विद्युत क्षत्रे क्या होगा।View Solution
- 22(i) दो विद्युतरोधी आवेषित गोले A तथा B जो आकार में सर्वसम हैं, के केन्द्रों के बीच की दूरी 50 सेमी. तथा दोनों पर पृथक-पृथक $6.5 \times 10^{-7}$ Cआवेष हैं। इसी प्रकार का एक अनावेषित गोला C सर्वप्रथम पहले गोले के सम्पर्क में तत्पष्चात दूसरे गोले के सम्पर्क में लाकर अन्ततः दोनों से हटा लिया जाता है। तब A तथा Bगोलों के मध्य लगने वाले प्रतिकर्षण बल का मान ज्ञात करो।View Solution
- 23View Solutionएक समानावेषित गोलीय कोष के कारण किसी बिन्दु पर विद्युत क्षेत्र की तीव्रता का परिकलन कीजिए जबकि बिन्दु स्थित है - (a) कोष के बाहर (b) कोष के पृष्ठ पर (c) कोष के अन्दर विद्युत क्षेत्र की तीव्रता का कोष के केन्द्र से दूरी के साथ परिवर्तन का आलेख भी दीजिए।
- 24View Solutionएक समान विद्युत क्षेत्र में स्थित विधुत द्विध्रुव पर तथा बलआघूर्ण के लिए व्यंजक स्थापित कीजिए। प्रत्येक स्थिति लिए बल आघूर्ण के मान को ज्ञात कीजिए।
- 25किसी बिन्दु पर स्थिर$-$वैद्युत की परिभाषा लिखिए। इसका $S.I.$ मात्रक भी लिखिए।View Solution
चित्र में दर्शाए अनुसार तीन बिन्दु आवेशों $q _1, q _2$ और $q_3$ क्रमशः बिन्दु $A, B$ और $C$ पर रखे हैं। इस निकाय की स्थिर$-$वैद्युत स्थितिज ऊर्जा के लिए व्यंजक व्युत्पन्न कीजिए। - 26त्रिज्या R के पतले गोलीय खोल का एकसमान पृष्ठीय आवेश घनत्व $\sigma$ है। इसके कारण निम्नलिखित परिस्थितियों में विद्युत क्षेत्र की तीव्रता का परिकलन कीजिए-View Solution
(i) खोल के बाहर विद्युत क्षेत्र
(ii) खोल के भीतर विद्युत क्षेत्र। - 27दो वैद्युत आवेश $+ Q$ तथा $Q (x - y)$ तल में क्रमशः बिन्दुओं $(- x_2, 0)$ तथा $(x_1, 0)$ पर रखे हैं। मूल बिन्दु $(0,0)$ पर परिणामी वैद्युत क्षेत्र का परिमाण तथा दिशा ज्ञात कीजिए।View Solution
- 28View Solutionकूलॉम बल (F) का (r) के साथ विचरण का ग्राफ खींचिये। जहाँ r प्रत्येक आवेश युग्म (1µC, 2C) तथा (2µC, -3µC) के दोनों आवेशों के बीच की दूरी है। प्राप्त ग्राफ की विवेचना कीजिए।
- 29View Solutionसमझाइए कि आवेश का क्वाण्टीकरण एवं आवेश का संरक्षण क्या है?
- 30View Solutionआवेश के गुणधर्म लिखिए। आवेश संरक्षण से क्या अभिप्राय है? उदाहरण द्वारा समझाइए। आवेश क्वाण्टीकरण से आप क्या समझते हैं?
- 31View Solutionवैद्युत आवेश को समझाइए। प्रयोग द्वारा सत्यापन कीजिए कि सजातीय आवेशों में प्रतिकर्षण और विजातीय आवेशों में आकर्षण होता है।
- 32View Solutionगाउस का प्रमेय क्या है? इसकी सहायता से अनच लम्बाई के समान रूप से आवेशित रेखीय चालक के निकट किसी बिन्द पर विधुत क्षेत्र की तीव्रता के लिए व्यंजक प्राप्तकीजिए। ###आवश्यक चित्र बनाकर गाउस के नियम की सहायता से अनन्त लम्बाई के आवेशित तार के कारण किसी बिन्दु पर विद्युत क्षेत्र की तीव्रता का परिकलन कीजिए। दूरी के साथ तीव्रता में परिवर्तन को आलेखित कीजिए।###गाउस के नियम को परिभाषित कीजिए। इसकी सहायता से अनन्त विस्तार के समरूप आवेशित रेखीय चालक से r दूरी पर विधुत क्षेत्र की तीव्रता का मान ज्ञात कीजिए। आवश्यक चित्र भी बनाइए और दूरी के साथ विधुत क्षेत्र के परिवर्तन का आलेख भी बनाइए।
- 33View Solutionआवेशों के स्थिति सदिशों के पदों में अध्यारोपण के सिद्धांत की व्याख्या कीजिए।
- 34View Solutionकूलॉम नियम के सदिश रूप की व्याख्या कीजिए और इसके महत्त्वपूर्ण तथ्यों को लिखिए।
- 35View Solution"विद्युत आवेश के इलेक्ट्रॉन सिद्धान्त" की व्याख्या कीजिए।
- 36View Solutionविधुतफ्लक्स की परिभाषा दीजिए। विधुत द्विध्रुव के कारण इसके अक्षीय बिन्दु के लिए विधुत क्षेत्र की तीव्रता का व्यंजक ज्ञात कीजिए। चित्र बनाइए।
- 37View Solutionविधुत फ्लक्स की परिभाषा लिखिए। गाउस के नियम द्वारा किसी एक समान रूप से आवेशित अनन्त विस्तार के सीधे तार - के कारण किसी बिन्दु पर विधुत क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए। आवश्यक चित्र बनाइए।
- 38View Solutionविधुत क्षेत्र रेखाओं से क्या अभिप्राय है? विभिन्न आवेश वितरणों के कारण विधुत क्षेत्र रेखाओं के उदाहरण दीजिए और इनकी विशेषताएँ भी लिखिए।
- 39View Solutionकूलॉम के नियम को प्रतिपादित कीजिए। इस नियम के आधार पर आवेश के मात्रक कूलॉम की परिभाषा लिखिए। यदि आवेशों के मध्य माध्यम हो तो विधुत बल माध्यम के साथ किस प्रकार बदलेगा?
- 40View Solutionवैद्युत द्विध्रुव के विषुवतीय तल पर स्थित किसी बिन्दु पर द्विध्रुव के कारण उत्पन्न विधुत क्षेत्र की व्युत्पत्ति कीजिए। आवश्यक चित्र बनाइए।
- 41View Solutionविधुत क्षेत्र की तीव्रता से क्या अभिप्राय है? इसका मात्रक एवं विमीय सूत्र लिखिए। बिन्दुवत् आवेश के कारण किसी बिन्दु पर विधुत क्षेत्र की तीव्रता का व्यंजक ज्ञात कीजिए। विद्युत क्षेत्र की तीव्रता E और दूरी r के मध्य आलेख खींचिए।
- 42View Solutionस्थिर-विधुतकी में गाउस का नियम लिखिए। उपयुक्त उदाहरण की सहायता से चित्र सहित यह दर्शाइए कि निर्वात में किसी बन्द पृष्ठ में बिन्दु आवेश 'q' के कारण बहिर्मुखी फ्लक्स पृष्ठ के आकार और आकृति पर निर्भर नहीं करता और इसका परिमाण q/६० होता है।
- 43View Solutionकोई बिन्दु P परं किसी विधुत द्विध्रुव के अक्ष पर उसके मध्य बिन्दु से x दूरी पर स्थित है। बिन्दु P पर विधुत विभव किसके समानुपाती होता है?
- 44View Solutionदो आवेश जिनमें प्रत्येक का आवेश + q है, एक-दूसरे से '2a' दूरी पर स्थित हैं। कोई तीसरा आवेश 2q इन दोनों के मध्य बिन्दु पर स्थित है। इन निकाय की स्थितिज ऊर्जा है-
- 45View Solutionएकसमान आवेशित एक गोलीय खोल के भीतर विधुत विभव (V) की दूरी पर निर्भरता होती है-
- 46संलग्न चित्र में तीन संधारित्र जिनकी क्रमशः धारिता $C_1, C_2$ और $C_3$ हैं, को बैटरी से संयोजित किया गया है, तो सत्य सम्बन्ध हैView Solution
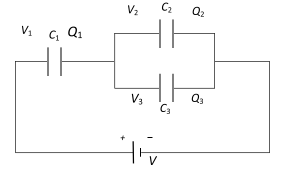
- 47View Solutionएक समान्तर प्लेट संधारित्र को सर्वप्रथम आवेशित किया जाता है। फिर इसकी प्लेटों के बीच परावैद्युतांक की पट्टिका रखी जाती है। अपरिवर्तित रहने वाली राशि है
- 48View Solutionएक आवेशित संधारित्र की प्लेटों के बीच किसी बिन्दु पर विद्युत क्षेत्र की तीव्रता
- 49View Solutionकिसी कुचालक का परावैद्युतांक नहीं हो सकता
- 50View Solutionसमान्तर प्लेट संधारित्र की धारिता बढती है
- 51View Solutionजब संधारित्र में परावैद्युत वायु के स्थान पर K परावैद्युतांक के पदार्थ को रखा जाता है, तो धारिता
- 52View Solutionक्या संधारित्र में परावैद्युत माध्यम के रुप में धातुओं का उपयोग कर सकते हैं
- 53View Solutionएक समान्तर प्लेट संधरित्र की धारिता C है, यदि उनकी प्लेटों के मध्य की दूरी आधी कर देते हैं, तो धारिता का मान होगा
- 54View Solutionसमान्तर प्लेट संधारित्र की धारिता निर्भर करती है
- 55View Solutionजब दो आवेषित चालकों पर परस्पर स्पर्ष कराया जाता है, तो
- 56View SolutionC धारिता के संधारित्र में संचित ऊर्जा क्या होगी, जबकि उसका विभव V तक बढ़ाया जाये
- 57View Solutionप्रत्येक आवेषित संधारित्र में ऊर्जा रहती है
- 58View Solutionकिसी आवेशित संधारित्र की स्थितिज ऊर्जा निम्न में से किस सूत्र से प्राप्त होती है (q = चालक पर आवेश, C = इसकी धारिता)
- 59View Solutionएक संधारित्र को बैटरी द्वारा आवेशित करके बैटरी को विच्छेद कर देते हैं। संधारित्रों के पट्टिकाओं के बीच डाइ-इलैक्ट्रिक (परावैद्युत) पट्ट सरकाते हैं, जिसके फलस्वरूप
- 60View Solution20 कूलॉम आवेष को बिन्दु A से B तक 0.2 मीटर तक लाने में किया गया कार्य 2 जूल है। दोनों बिन्दुओं के मध्य विभवान्तर है
- 61View Solution5 कूलॉम का एक आवेश 0.5m से विस्थापित किया जाता है। इस प्रक्रिया में किया गया कार्य 10 जूल है। दोनों बिन्दुओं के बीच विभवान्तर होगा
- 62View Solutionविद्युत द्विध्रुव के कारण किसी बिन्दु पर विभव अधिकतम तथा न्यूनतम होगा जब द्विध्रुव अक्ष तथा बिन्दु व द्विध्रुव को मिलाने वाली रेखा के मध्य कोण क्रमषः हों
- 63View Solutionकिसी चालक गोले के अन्दर विद्युत विभव
- 64View Solutionपृथ्वी का विद्युत विभव शून्य माना जाता है क्योंकि पृथ्वी एक
- 65View Solutionएक बिन्दु आवेश के कारण किसी बिन्दु पर विभव का मान होगा
- 66View Solutionदो आवेश +q और -q एक निश्चित दूरी पर हैं, उनके बीचों बीच स्थित बिन्दु पर
- 67View Solutionसमविभव पृष्ठ तथा विद्युत बल रेखाओं के बीच कोण है
- 68दो सर्वसम लघु चालक गेंदों $B_1$और $B_2$ को क्रमशः $-7 pC.$ और $+ 4 PC$ आवेश दिए गए हैं। इन दोनों को किसी तीसरी सर्वसम गेंद $B_3$ द्वारा सम्पर्क में लाकर फिर पृथक कर दिया गया है। अब यदि सभी गेंदों पर अन्तिम आवेश $- 2 pC$ है, तो $B_3$ पर प्रारम्भिक आवेश क्या था$?$View Solution
- 69View Solutionएक आवेशित संधारित्र की दोनों प्लेटों को एक तार से जोड़ दिया जाये तो-
- 70View Solution(8 µF-250V) अंकित अनेक संधारित्र दिये गये हैं। एक (16 µF - 1000V) की तुल्यधारिता प्राप्त करने के लिए आवश्यक संधारित्रों की न्यूनतम संख्या होगी-
- 71$C_1$ तथा $C_2$ धारिता के दो संधारित्रों के समान्तर संयोजन को $Q$ आवेश दिया जाता है। $C_1$ पर $Q_1$ तथा $C_2$ पर $Q_2 $आवेश होने पर $\frac{ Q _1}{ Q _2}$ का अनुपात होगा$-$View Solution
- 72View Solutionशंकु की आकृति के सुचालक वस्तु का आवेश घनत्व अधिकतम होगा-
- 73समान्तर प्लेट संधारित्र की प्लेटों के मध्य के स्थान के आधे भाग में $\epsilon_{ r }$, परावैद्युतांक माध्यम भरा हुआ है। यदि हवा वाले भाग की धारिता C है तो सम्पूर्ण संधारित्र निकाय की धारिता होगी-View Solution
- 74एक आवेशित समान्तर प्लेट संधारित्र में $U _0$ विधुत ऊर्जा संग्रहित है। संधारित्र की प्लेटों के बीच की दूरी को दुगुना करने पर विधुत ऊर्जा होगी-View Solution
- 75एक समान्तर पट्ट संधारित्र की प्लेटों के बीच समरूप क्षेत्र $E$ वोल्ट/मीटर है। यदि प्लेटों के बीच की दूरी $d ($मी$)$ तथा प्रत्येक प्लेट का क्षेत्रफल $A ($मी$^2)$ है तो उसमें संचित कुल ऊर्जा है$-$View Solution
- 76View Solutionदिये गये चित्र में प्रत्येक संधारित्र की धारिता x है। बिन्दु A व B के मध्य तुल्यधारिता होगी-

- 77View Solutionयदि एक धन आवेश को निम्न विभव के क्षेत्र से उच्च विभव के क्षेत्र में ले जाया जाता है तो विधुत स्थितिज ऊर्जा-
- 78View Solutionएक समबाहु त्रिभुज के तीन कोनों पर समान आवेश स्थित है। त्रिभुज के केन्द्र 0 पर विधुत विभव V तथा विधुत क्षेत्र की तीव्रता E के लिए सत्य कथन होगा-
- 79View Solutionदो बिन्दुओं के मध्य की दूरी 30 सेमी. है। यदि बिन्दु A पर 20 μC आवेश व B पर -10 µC आवेश पर रखा हुआ है तो A व B के बीच किस बिन्दु पर विभव शून्य होगा-
- 80View Solutionविभवान्तर V, आवेश Q तथा धारिता C में सम्बन्ध है-
- 81View Solutionसमविभव पृष्ठ में से पारित फ्लक्स हमेशा-
- 82एक C धारिता का तथा दूसरा$\frac{C}{2}$ धारिता का संधारित्र एक V वोल्ट की बैटरी से चित्र के अनुसार जोड़े गये हैं। दोनों संधारित्रों को पूर्णतया आवेशित करने में किया गया कार्य है-View Solution

- 83View Solutionदो समान आवेश q एक-दूसरे से d दूरी पर रखे हैं। इनके मध्य दूरी पर स्थित बिन्दु पर विभव होगा-
- 84किसी माध्यम की पराविधुतशक्ति $2\ kV\ mm^{-1}$ है। $50\ µm$ के नमूने में बिना बंधे कितना अधिकतम विभवान्तर स्थापित किया जा सकता है$?$View Solution
- 85View Solutionपानी की आवेशित 64 बूंदों को मिलाकर एक बड़ी बूंद बना ली जाती है तो बड़ी बूंद पर विभव का मान पूर्ण मान से कितने गुना होगा?
- 86View Solutionएक E = 0 वाले विधुत क्षेत्र की तीव्रता में विधुत विभव का दूरी के साथ परिवर्तन होगा-
- 87View Solution2µF के तीन संधारित्रों को समान्तर क्रम में जोड़ने पर तुल्यधारिता होगी-
- 88दो संधारित्रों की धारितायें $C_1$ तथा $C_2$ में संग्रहित ऊर्जायें रामान हैं। संधारित्रों पर विभवान्तर का अनुपात होगा$-$View Solution
- 89View Solutionसंधारित्र में ऊर्जा किस स्वरूप में उपस्थित होती है?
- 90View Solutionछोटी 64 बूँदें मिलकर एक बड़ी बूँद बनाती हैं। यदि प्रत्येक छोटी बूँद पर Q आवेश हो तो बड़ी बूँद पर आवेश होगा-
- 91View Solutionएक संधारित्र की धारिता C है। इसे V विभवान्तर पर आवेशित किया गया है। यदि अब इसे प्रतिरोध से सम्बन्धित कर दिया जाये, ऊर्जा क्षय की मात्रा होगी-
- 92View Solutionधातु के एक आवेशित ठोस गोले के केन्द्र पर विधुत विभव है-
- 93View Solutionपृथ्वी का विधुत विभव माना गया है-
- 94View Solutionतीन संधारित्रों को किस क्रम में जोड़ा जाए कि उनमें समान विभव पर संचित ऊर्जा अधिकतम हो-
- 95View Solutionसमान त्रिज्या के ताँबे के खोखले गोले A व ठोस गोले B को एक समान विभव से आवेशित किया गया है। सत्य कथन है-
- 96View Solution5 माइक्रो फैरड धारिता के एक संधारित्र को 1000 वोल्ट तेह आवेशित किया जाता है। संधारित्र पर संचित ऊर्जा होगी-(जूल में)
- 97View Solutionएक समान त्रिज्या एवं समान आवेशयुक्त पानी को 27 छोटी बूंदें मिलकर एक बड़ी बूंद बनाती हैं। बड़ी बूंद की धारिता तथा एक छोटी बूंद की धारिता का अनुपात होगा-
- 98View Solution10µF धारित के समान्तर प्लेट संधारित्र को 40µc आवेश देने पर उसकी कुल ऊर्जा का मान जूल में होगा-
- 99View Solutionआवेशित संधारित्र में संग्रहित ऊर्जा होती है-
- 100View Solutionसंलग्न चित्र में बिन्दुओं A व B के बीच तुल्य धारिता का मान होगा-
