Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1यदि $\vec{a} \vec{b} \vec{c}$ इकाई सदिश हो जिसमें कि $\vec{a}+\vec{b}+\vec{c}=0$ तो $\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}$ का मान है :View Solution
- 2यदि $x \vec{i}-3 \vec{j}+5 \vec{k}$ एवं $-x \vec{i}+x \vec{j}+2 \vec{k}$ परस्पर लंब हो तो $x=$View Solution
- 3सदिश $3 \vec{i}-4 \vec{j}+12 \vec{k}$ दिक् कोज्याएँ हैं :View Solution
- 4$\vec{a} \times(\vec{b} \times \vec{c})=$View Solution
- 5$\vec{i} \times(\vec{i} \times \vec{j})+\vec{j} \times(\vec{j} \times \vec{k})+\vec{k} \times(\vec{k} \times \vec{i})=[$ [BSEB, $2018(\mathrm{~A})]$View Solution
- 6सदिशों $2 \vec{i}-3 \vec{j}+2 \vec{k}$ एवं $\vec{i}+4 \vec{j}+5 \vec{k}$ के बीच का कोण है-View Solution
- 7दो सदिश $2 \vec{i}+5 \vec{j}+\vec{k}$ और $3 \vec{i}-2 \vec{j}+4 \vec{k}$ है :View Solution
- 8मूल बिन्दु से $(-3,4,5)$ की दूरी है :View Solution
- 9$\vec{i} \cdot(\vec{j} \times \vec{k})+\vec{j} \cdot(\vec{i} \times \vec{k})+\vec{k} \cdot(\vec{i} \times \vec{j})=$View Solution
- 10यदि $\vec{a}$ और $\vec{b}$ कोई दो सदिश हों, तो $(\vec{a} \times \vec{b})^2$ बराबर है :View Solution
- 11यदि $\vec{a}=\vec{i}-2 \vec{j}-3 \vec{k}, \vec{b}=\vec{i}+3 \vec{j}-2 \vec{k}$ तो $\vec{a} \cdot \vec{b}=$ :View Solution
- 12यदि $|\vec{a}|=|\vec{b}|=|\vec{a}+\vec{b}|=1$ तो $|\vec{a}-\vec{b}|$ बराबर है :View Solution
- 13$(\vec{a}-\vec{b}) \times(\vec{a}+\vec{b})$ के स्थान पर निम्नांकित में कौन-सा लिखा जा सकता है ?View Solution
- 14$\vec{a} \vec{b} \vec{c}$ एकतलीय होंगे, यदि :View Solution
- 15सदिशों $2 \vec{i}-3 \vec{j}+2 \vec{k}$ एवं $\vec{i}+4 \vec{j}+5 \vec{k}$ के बीच का कोण है :View Solution
- 16$\overline{\mathrm{k}} \times \overline{\mathrm{j}}=$View Solution
- 17यदि मूल बिन्दु $\mathrm{O}$ हो तथा $\overline{\mathrm{OP}}=2 \hat{i}+3 \hat{j}-4 \hat{k}$ तथा $\overline{\mathrm{OQ}}=5 \hat{i}+4 \hat{j}-3 \hat{k}$ हों, तो $\overline{\mathrm{PQ}}$ समान है :View Solution
- 18बिंदु $(1,0,2)$ का स्थिति सदिश है :View Solution
- 19$5 \hat{\mathrm{i}}+\hat{\mathrm{j}}-3 \hat{\mathrm{k}}$ और $3 \overrightarrow{\mathrm{i}}-4 \overrightarrow{\mathrm{j}}+7 \overrightarrow{\mathrm{k}}$ का अदिश गुणनफल है :View Solution
- 20यदि $\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}=0$ हो, तोView Solution
- 21यदि $|\overrightarrow{\mathrm{a}}|=\sqrt{26},|\overrightarrow{\mathrm{b}}|=7$ और $|\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}|=35$ तो $\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}=$View Solution
- 22यदि $|\bar{a}+\bar{b}|=|\bar{a}-\bar{b}|$ तो :View Solution
- 23$7 \vec{i}-2 \vec{j}+\vec{k}$ का मापांक है :View Solution
- 24$\hat{\mathrm{i}}-2 \hat{\mathrm{j}}+\hat{\mathrm{k}}$ पर सदिश $2 \hat{\mathrm{i}}-\hat{\mathrm{j}}+\hat{\mathrm{k}}$ का प्रक्षेप है :View Solution
- 25सदिश $2 \overrightarrow{\mathrm{i}}-7 \overrightarrow{\mathrm{j}}-3 \overrightarrow{\mathrm{k}}$ का मापांक है :View Solution
- 26बिन्दु $(3,4,-2)$ और $(5,6,-3)$ को मिलाने वाली रेखा पर सदिश $2 \hat{i}-3 \hat{j}-6 \hat{k}$ प्रक्षेप है :View Solution
- 27यदि $\mathrm{a}=\overline{\mathrm{i}}+2 \overline{\mathrm{j}}+3 \overline{\mathrm{k}}$ और $\mathrm{b}=3 \mathrm{i}+2 \mathrm{j}+\mathrm{k}$ तो $\cos \theta=$View Solution
- 28यदि $\overrightarrow{\mathrm{a}}=2 \overline{\mathrm{i}}-5 \overrightarrow{\mathrm{j}}+\overline{\mathrm{k}}$ और $\overrightarrow{\mathrm{b}}=4 \overline{\mathrm{i}}+2 \overline{\mathrm{j}}+\overline{\mathrm{k}}$ तो $\overrightarrow{\mathrm{a}} \cdot \overline{\mathrm{b}}=$View Solution
- 29यदि $a=2 \bar{i}-3 \bar{j}+4 \bar{k}$ और $b=\bar{i}+2 \bar{j}+\bar{k}$ तो $\bar{a}+\bar{b}=$View Solution
- 30$\vec{a} \times \vec{a}=$View Solution
- 31$|-\vec{i}+2 \vec{j}-3 \vec{k}|=$View Solution
- 32$\vec{k} \times \vec{k}=$View Solution
- 33$(\vec{a} \times \vec{a}) \cdot \vec{b}$View Solution
- 34$(\vec{a}+\vec{b}) \cdot(\vec{a}-\vec{b})=$View Solution
- 35$\vec{i} \cdot \vec{j}=$View Solution
- 36यदि $\overrightarrow{O A}=2 \vec{i}+5 \vec{j}-2 \vec{k}$ तथा $\overrightarrow{O B}=3 \vec{i}+6 \vec{j}+5 \vec{k}$ तो $\overrightarrow{A B}=$View Solution
- 37$j \times k=$View Solution
- 38यदि बिन्दु $\mathrm{A}$ और $\mathrm{B}$ के स्थिति सदिश क्रमशः $(1,2,3)$ और $(-3,-4,0)$ हो, तो $\overrightarrow{A B}=$View Solution
- 39बिन्दु $(4,5,6)$ का स्थिति सदिश है :View Solution
- 40$\vec{a} \cdot \vec{b}=$View Solution
- 41यदि $\vec{a}=3 \vec{i}+2 \vec{j}+\vec{k}, \vec{b}=4 \vec{i}-5 \vec{j}+3 \vec{k}$, तो $\vec{a} \cdot \vec{b}=$View Solution
- 42यदि $\vec{a}$ और $\vec{b}$ परस्पर लम्ब हों तो :View Solution
- 43$\vec{j} \times \vec{i}=$View Solution
- 44यदि दो सदिशों $\vec{a}$ और $\vec{b}$ के बीच का कोण $\theta$ है तो |$\vec{a}$ $\cdot$ $\vec{b}$| = |$\vec{a}$ $\times$ $\vec{b}$| जब $\theta$ बराबर है:View Solution
- 45$\hat{i} \cdot(\hat{j} \times \hat{k})+\hat{j} \cdot(\hat{i} \times \hat{k})$ + $\hat{k} \cdot(\hat{i} \times \hat{j})$ का मान हैView Solution
- 46मान लीजिए $\vec{a}$ और $\vec{b}$ दो मात्रक सदिश हैं और उनके बीच का कोण $\theta$ है तो $\vec{a}+\vec{b}$ एक मात्रक सदिश है यदि:View Solution
- 47यदि दो सदिशों $\vec{a}$ और $\vec{b}$ के बीच का कोण $\theta$ है तो $\vec{a}$ $\cdot$ $\vec{b}$ $\geq$ 0 होगा यदि:View Solution
- 48एक आयत के शीर्षों A, B, C और D जिनके स्थिति सदिश क्रमश: $-\hat{i}+\frac{1}{2} \hat{j}+4 \hat{k}$, $\hat{i}+\frac{1}{2} \hat{j}+4 \hat{k}$, $\hat{i}-\frac{1}{2} \hat{j}+4 \hat{k}$ और $-\hat{i}-\frac{1}{2} \hat{j}+4 \hat{k}$, हैं का क्षेत्रफल है:View Solution
- 49मान लीजिए सदिश $\vec{a}$ और $\vec{b}$ इस प्रकार हैं कि $|\vec{a}|=3$ और $|\vec{b}|$ = $\frac{\sqrt{2}}{3}$, तब $\vec{a} \times \vec{b}$ एक मात्रक सदिश है यदि $\vec{a}$ और $\vec{b}$ के बीच का कोण है:View Solution
- 50यदि $\vec{a}$ और $\vec{b}$ दो संरेख सदिश हैं तो निम्नलिखित में से कौन सा कथन सही नहीं है:View Solution
- $\vec{b}$ = $\lambda$ $\vec{a}$, किसी अदिश $\lambda$ के लिए
- $\vec{a}$ = $\pm \vec{b}$
- $\vec{a}$ और $\vec{b}$ के क्रमागत घटक समानुपाती नहीं हैं।
- दोनों सदिशों $\vec{a}$ तथा $\vec{b}$ की दिशा समान है परंतु परिमाण विभिन्न हैं।
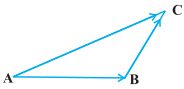
- 51View Solutionत्रिभुज ABC आकृति, के लिए निम्नलिखित में से कौन सा कथन सत्य नहीं है।
- 52View Solutionसमान परिमाण वाले दो संरेख सदिश समान होते हैं।
- 53View Solutionसमान परिमाण वाले दो सदिश संरेख होते हैं।
- 54View Solutionदो संरेख सदिशों का परिमाण सदैव समान होता है।
- 55$\vec{a}$ तथा $-\vec{a}$ संरेख हैं।View Solution
- 56View Solutionआकृति (एक वर्ग) में संरेख परंतु असमान सदिश को पहचानिए।
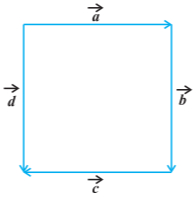
- 57View Solutionआकृति (एक वर्ग) में समान सदिश को पहचानिए।

- 58View Solutionआकृति (एक वर्ग) में सह-आदिम सदिश को पहचानिए।

- 59View Solutionकार्य को अदिश एवं सदिश राशियों के रूप में श्रेणीबद्ध कीजिए।
- 60View Solutionवेग को अदिश एवं सदिश राशियों के रूप में श्रेणीबद्ध कीजिए।
- 61View Solutionबल को अदिश एवं सदिश राशियों के रूप में श्रेणीबद्ध कीजिए।
- 62View Solutionदूरी को अदिश एवं सदिश राशियों के रूप में श्रेणीबद्ध कीजिए।
- 63View Solutionसमय कालांश को अदिश एवं सदिश राशियों के रूप में श्रेणीबद्ध कीजिए।
- 64$20\ m/s^2$ माप को अदिश एवं सदिश के रूप में श्रेणीबद्ध कीजिए।View Solution
- 65$10^{-19}$ कूलंब माप को अदिश एवं सदिश के रूप में श्रेणीबद्ध कीजिए।View Solution
- 66View Solution40 वाट माप को अदिश एवं सदिश के रूप में श्रेणीबद्ध कीजिए।
- 67$40^\circ$ माप को अदिश एवं सदिश के रूप में श्रेणीबद्ध कीजिए।View Solution
- 68View Solution2 मीटर उत्तर-पश्चिम माप को अदिश एवं सदिश के रूप में श्रेणीबद्ध कीजिए।
- 69View Solution10kg माप को अदिश एवं सदिश के रूप में श्रेणीबद्ध कीजिए।
- 70उत्तर से $30^\circ$ पूर्व में $40\ km$ के विस्थापन का आलेखीय निरूपण कीजिए।View Solution
- 71View Solutionआकृति में कौन से सदिश सह-आदिम हैं।
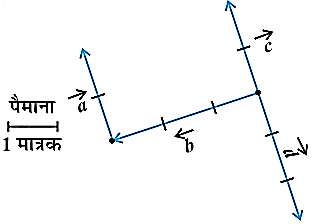
- 72View Solutionआकृति में कौन से सदिश समान हैं।

- 73View Solutionआकृति में कौन से सदिश संरेख हैं।

- 74View Solution20m/s उत्तर की ओर माप को अदिश एवं सदिश के रूप में श्रेणीबद्ध कीजिए।
- 75$10\ g\ cm^3$ माप को अदिश एवं सदिश के रूप में श्रेणीबद्ध कीजिए।View Solution
- 76View Solution30km/h माप को अदिश एवं सदिश के रूप में श्रेणीबद्ध कीजिए।
- 77View Solution10 N माप को अदिश एवं सदिश के रूप में श्रेणीबद्ध कीजिए।
- 78$1000\ cm^3$ माप को अदिश एवं सदिश के रूप में श्रेणीबद्ध कीजिए।View Solution
- 79View Solution5s माप को अदिश एवं सदिश के रूप में श्रेणीबद्ध कीजिए।
- 80दो बिंदु P और Q लीजिए जिनके स्थिति सदिश $\vec{\mathrm{OP}}$ = $3 \vec{a}-2 \vec{b}$ और $\vec{\mathrm{OQ}}$ = $\vec{a}+\vec{b}$ हैं। एक ऐसे बिंदु R का स्थिति सदिश ज्ञात कीजिए जो P एवं Q को मिलाने वाली रेखा को 2 : 1 के अनुपात में बाह्य विभाजित करता है।View Solution
- 81दो बिंदु P और Q लीजिए जिनके स्थिति सदिश $\overrightarrow{\mathrm{OP}}$ = $3 \vec{a}-2 \vec{b}$ और $\overrightarrow{\mathrm{OQ}}$ = $\vec{a}+\vec{b}$ हैं। एक ऐसे बिंदु R का स्थिति सदिश ज्ञात कीजिए जो P एवं Q को मिलाने वाली रेखा को 2 : 1 के अनुपात में अंतः विभाजित करता है।View Solution
- 82दक्षिण से $30^\circ$ पश्चिम में, $40\ km$ के विस्थापन का आलेखीय निरूपण कीजिए।View Solution
- 83यदि $\vec{a}$ = $\hat{i}+\hat{j}+\hat{k}$, $\vec{b}$ = $2 \hat{i}-\hat{j}+3 \hat{k}$ और $\vec{c}$ = $\hat{i}-2 \hat{j}+\hat{k}$, तो सदिश $2 \vec{a}-\vec{b}+3 \vec{c}$ के समांतर एक मात्रक सदिश ज्ञात कीजिए।View Solution
- 84x का वह मान ज्ञात कीजिए जिसके लिए x$(\hat{i}+\hat{j}+\hat{k})$ एक मात्रक सदिश है।View Solution
- 85बिंदु P$\left(x_{1}, y_{1}, z_{1}\right)$ और Q$\left(x_{2}, y_{2}, z_{2}\right)$ को मिलाने वाले सदिश के अदिश घटक और परिमाण ज्ञात कीजिए।View Solution
- 86सिद्ध कीजिए कि $(\vec{a}+\vec{b}) \cdot(\vec{a}+\vec{b}) = |\vec{a}|^{2}+|\vec{b}|^{2}$, यदि और केवल यदि $\vec{a}, \vec{b}$ लंबवत् हैं। यह दिया हुआ है कि $\vec{a}$View Solution
$\neq$
$\vec{0}, \vec{b}$
$\neq$
$\vec{0}$. - 87दर्शाइए कि OX, OY एवं OZ अक्षों के साथ बराबर झुके हुए सदिश की दिक्-कोसाइन कोज्याएँ $\pm\left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right)$ है।View Solution
- 88$XY-$तल में$, x-$अक्ष की धनात्मक दिशा के साथ वामावर्त दिशा में $30^\circ$ का कोण बनाने वाला मात्रक सदिश लिखिए।View Solution
- 89यदि $\vec{a} = \vec{0}$ अथवा $\vec{b} = \vec{0}$ तब $\vec{a} \times \vec{b} = \vec{0}$ होता है। क्या विलोम सत्य है? उदाहरण सहित अपने उत्तर की पुष्टि कीजिए।View Solution
- 90दिया हुआ है कि $\vec{a} \cdot \vec{b}$ = 0 और $\vec{a} \times \vec{b}$ = $\vec{0}$ सदिश $\vec{a}$ और $\vec{b}$ के बारे में आप क्या निष्कर्ष निकाल सकते हैं?View Solution
- 91$\lambda$ और $\mu$ ज्ञात कीजिए, यदि $(2 \hat{i}+6 \hat{j}+27 \hat{k})$ $\times$ $(\hat{i}+\lambda \hat{j}+\mu \hat{k})$ = $\vec{0}$View Solution
- 92दर्शाइए कि $(\vec{a}-\vec{b}) \times(\vec{a}+\vec{b})$ = $2(\vec{a} \times \vec{b})$View Solution
- 93एक समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसकी संलग्न भुजाएँ सदिश $\vec{a}$ = $\hat{i}-\hat{j}+3 \hat{k}$ और $\vec{b}$ = $2 \hat{i}-7 \hat{j}+\hat{k}$ द्वारा निर्धारित हैं।View Solution
- 94यदि $\vec{a}$ = $\hat{i}-7 \hat{j}+7 \hat{k}$ और $\vec{b}$ = $3 \hat{i}-2 \hat{j}+2 \hat{k}$ तो |$\vec{a} \times \vec{b}$| ज्ञात कीजिए।View Solution
- 95यदि एक मात्रक सदिश $\vec{a}$, के लिए $(\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a}) = 12$ हो तो $|\vec{x}|$ ज्ञात कीजिए।View Solution
- 96दो सदिशों $\vec{a}$ और $\vec{b}$ के परिमाण ज्ञात कीजिए, यदि इनके परिमाण समान है और इन के बीच का कोण $60^\circ$ है तथा इनका अदिश गुणनफल $\frac{1}{2}$ है।View Solution
- 97$(3 \vec{a}-5 \vec{b}) \cdot(2 \vec{a}+7 \vec{b})$ का मान ज्ञात कीजिए।View Solution
- 98सदिश $\hat{i}+3 \hat{j}+7 \hat{k}$ का, सदिश $7 \hat{i}-\hat{j}+8 \hat{k}$ पर प्रक्षेप ज्ञात कीजिए।View Solution
- 99सदिश $\hat{i}+\hat{j}$ पर सदिश $\hat{i}-\hat{j}$ का प्रक्षेप ज्ञात कीजिए।View Solution
- 100यदि $\vec{a}$ = $\overrightarrow{0}$ अथवा $\vec{b}$ = $\vec{0}$, तब $\vec{a} \cdot \vec{b}$ = 0 परंतु विलोम का सत्य होना आवश्यक नहीं है। एक उदाहरण द्वारा अपने उत्तर की पुष्टि कीजिए।View Solution