Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1પ્રકમ $CO_2$$_{(s)}$ $\rightarrow$ $CO_2$$_{(g)}$ માટે ..... સાચું છે.View Solution
- 2પ્રકિયા $3F{e_{\left( s \right)}} + 4{H_2}{O_{\left( g \right)}} \rightleftharpoons F{e_3}{O_{4\left( s \right)}} + 4{H_{2\left( g \right)}}$ એ પ્રતિવર્તી ત્યારે થશે જ્યારે તે ................ કરવામાં આવે.View Solution
- 3પ્રક્રિયક અને નિપજની કુલ એન્થાલ્પી અનુક્રમે $H_R$ અને $H_P$ છે. તો ઉષ્માક્ષેપક પ્રક્રિયા માટે ...... થાય.View Solution
- 4પ્રક્રિયા $A + B$ $\rightarrow$ $C + D + q $ જે ઘન એન્ટ્રોપી ફેરફાર ધરાવે છે. તો પ્રક્રિયા........View Solution
- 5પ્રક્રિયા $A+B \rightarrow C+D+q$ નો એન્ટ્રોપી ફેરફાર ધન જણાયો છે. પ્રક્રિયાView Solution
- 6View Solutionપ્રક્રિયા દરમ્યાન એન્થાલ્પીનો ફેરફાર ....... પર આધારિત નથી.
- 7View Solutionપ્રક્રિયાનો સ્યંભૂ ગુણધર્મ અશક્ય છે. જો ........
- 8...... પ્રક્રિયામાં $\Delta S$ ઋણ છે.View Solution
- 9...... પ્રક્રિયામાં $\Delta$$S$ ધન છે.View Solution
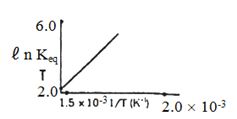
- 10પ્રક્રિયા માટે $ℓ\,n\, K_{eq}$ વિરૂદ્ધ તાપમાનનો આલેખ દોરવામાં આવે તો પ્રક્રિયા...... હોવી જોઈએ.View Solution
- 11View Solutionપ્રક્રિયા માટે એન્થાલ્પીનો ફેરફાર ........ પર આધારિત નથી.
- 12View Solutionપ્રક્રિયા માટે જ્યારે એન્થાલ્પીને પ્રાયોગિક રીતે ગણવી શક્ય ન હોય ત્યારે ..... દ્વારા એન્થાલ્પી ગણી શકાય છે.
- 13View Solutionપ્રક્રિયા માટે સંતુલન અચળાંક અને મુક્ત ઉર્જા વચ્ચેનો સાચો સંબંધ ....... છે.
- 14પ્રક્રિયામાં મુક્ત ઉર્જાનો ફેરફાર અને સંકળાયેલ સંતુલન અચળાંક $K_c$ વચ્ચેનો સાચો સંબંધ .......View Solution
- 15View Solutionપ્રણાલીનુ તાપમાન ....... પ્રકમમાં ધટે છે.
- 16પ્રણાલી પર $5\, KJ$ કાર્ય પૂર્ણ થાય અને $1\, KJ $ ઉષ્મા પ્રણાલી દ્વારા બહાર આવે છે. આ કિસ્સામાં આંતરિક ઊર્જાનો ફેરફાર ............ $\mathrm{kJ}$ માં શોધો.View Solution
- 17View Solutionપ્રણાલીમાંથી વાતાવરણમાં ઊર્જા રૂપાંતર કરી શકાય છે જેમ કે કાર્ય જો.....
- 18View Solutionપ્રતિવર્તી પ્રકમમાં કઇ શરતે વિનિમય પામતી ઉષ્મા અવસ્થા વિધેય બને છે ?
- 19View Solutionપ્રતિવર્તીં પ્રક્રિયા જે....
- 20View Solutionપ્રતિવર્તીં સમતાપી પ્રક્રમમાં આંતરિય ઊર્જાનો ફેરફાર ...... થાય છે.
- 21View Solutionપ્રતિવર્તીં સમોષ્મી પરિસ્થિતિ હેઠળ વાયુનું વિસ્તરણ થાય છે તો પ્રક્રિયા માટે શું શુન્ય થશે ?
- 22પ્રમાણિત મુક્ત ઊર્જા ફેરફાર અને સંતુલન અચળાંક $(Kp)$ વચ્ચેનો યોગ્ય સંબંધ ...... છે.View Solution
- 23પ્રાણાલીનું કદ અચળ ધારતાં સંતુલને ક્રીપ્ટોન $(Kr)$ વાયુ ઉમેરતા શું અસર થાય છે ?View Solution
- 24View Solutionબે મોલ આદર્શ વાયુનું શુન્યવકાશમાં સ્વયંભુ વિસ્તરણ થાય તો કાર્ય ...... જુલ થાય?
- 25બે સંયોજનો $x$ અને $y$ ની સર્જન ઉષ્મા અનુક્રમે $-84\, KJ$ અને ${-1}$$56\, KJ$ છે. તો નીચેનામાંથી કયું વિધાન સાચું છે ?View Solution
- 26View Solution........ માટે એન્ટ્રોપીનો ફેરફાર ઋણ હોય છે.
- 27View Solution‘રાસાયણિક પ્રક્રિયામાં થતો કુલ એન્થાલ્પી ફેરફાર એ પ્રક્રિયાના જુદા જુદા તબક્કાઓની એન્થાલ્પી ફેરફારના બેઝિક સરવાળા બરાબર હોય છે.’ આ વિધાન સાથે સંકળાયેલ વૈજ્ઞાનિક ...... હતા.
- 28રૂપાંતરણ માટે $C$(ગ્રેફાઈટ) $\rightarrow$ $C$(હિરો), $\Delta S$ .......View Solution
- 29View Solution...... વચ્ચેની પ્રક્રિયામાં તટસ્થીકરણ એન્થાલ્પીનું મૂલ્ય સૌથી ઓછું હોય છે.
- 30View Solution...... વચ્ચેની પ્રક્રિયામાં તટસ્થીકરણ એન્થાલ્પીનું મૂલ્ય સૌથી વધુ હોય છે.
- 31View Solutionવાયુના અપ્રતિવર્તી વિતરણમાં વાયુ દ્વારા થતુ કાર્ય..... થશે.
- 32View Solutionવાયુ સમીકરણ માટે આઈસો બ્યુટેનના સંપર્ણ દહન દરમિયાન......
- 33View Solutionવિશિષ્ટ ઉષ્મા ...... રીતે સમજાવાય.
- 34View Solutionસમતાપી પ્રકમ માટે નીચેનામાંથી શું સાચું છે ?
- 35View Solutionસમતાપી પ્રક્રમ દરમિયાન ...... થાય.
- 36સમાન તાપમાને $CH_4, C_2H_6, C_2H_4$ અને $C_2H_2$ વાયુઓની દહન ઉષ્મા અનુક્રમે $-212.8, -373.0, -337.0$ અને $-310.5\, Kcal$ છે. તો આ વાયુઓ પણ શ્રેષ્ઠ બળતણ કયું છે?View Solution
- 37View Solutionસમોષ્મી પ્રકમ ................. હોય છે.
- 38View Solutionસમોષ્મી પ્રક્રમ ...... પ્રણાલી દ્વારા અનુભવાય છે.
- 39View Solutionસમોષ્મી પ્રક્રિયા માટે નીચેનામાંથી કયો સંબંધ સાચો છે ?
- 40View Solutionસમોષ્મી વિસ્તરણ કરતા સમતાપી પ્રકમમાં વાયુના દબાણના ઘટાડા સાથે કદનો વધારો વધારે હોય છે, કારણ કે .............
- 41View Solutionસાચો ઉત્તર પસંદ કરો. ઉષ્માગતિય અવસ્થા વિધેય .............. રાશિ છે.
- 42View Solution...... સૂત્ર યોગ્ય છે.
- 43View Solutionસ્મોષ્મી પરિસ્થિતિ હેઠળ થનાર પ્રક્રમને માટે સાચી શરત છે :
- 44View Solutionસ્વયંભુ પ્રક્રિયાને લાગુ પડતું સાચુ વિધાન ઓળખો.
- 45View Solutionસ્વયંભૂ પ્રક્રિયા થવા માટે.......
- 46સ્વયંભૂ પ્રક્રિયા માટે $\Delta G$ સંતુલન અચળાંક $(K)$ અને $E^o_{cell}$ શું થાય?View Solution
- 47હિરાના કાર્બનની સંક્રાંતિથી ગ્રેફાઈટના કાર્બનનું બનવા માટે $\Delta$ $H - 453.5$ કેલરી છે જે શું દર્શાવે છે ?View Solution
- 48View Solutionહેઝના નિયમ મુજબ પ્રક્રિયાની ઊર્જા શેના પર આધાર રાખે છે ?
- 49View Solutionહેસનો ઉષ્માસંકલનનો નિયમ ઉષ્માગતિશાસ્ત્રના કયા નિયમને આધારે સમજાવી શકાય છે ?
- 50$0.8\,g$ કાર્બનનુ કાર્બન ડાયોક્સાઇડમાં રૂપાંતર થતા મુકત થતી ઉષ્મા $x\, cal$ છે. અને $0.8\,g$ કાર્બનનુ કાર્બન મોનોક્સાઇડમાં રૂપાંતર થતા મુક્ત થતી ઉષ્માં $y\, cal$ છે. જો $x > y$ હોય, તો $1.86\, g$ કાર્બન મોનોક્સાઇડનુ કાર્બન ડાયોક્સાઇડમાં રૂપાંતર થાય ત્યારે મુક્ત થતી ઉષ્માં ............ થશે.View Solution
- 51$1$ વાતાવરણ અચળ દબાણે સિલિન્ડરમાં રહેલ ઘર્ષણ રહિત પિસ્ટન વાયુને $2$ લીટર કદમાંથી $6$ લિટર કદમાં પ્રસરણ પામે છે. આમ થવાથી વાતાવરણમાંથી તે $800$ જૂલ ઉષ્મા અવશોષે છે. તો પ્રક્રિયામાં આંતરિક ઊર્જા થતો વધારાનું માપન .....$J$ થશે.View Solution
- 52$25$ $^o$$C$ અને $1$ વાતાવરણ દબાણે $C_2H_4$$_{(g)}$, $CO_2$$_{(g)}$ અને $H_2O$ $_{(l)}$ ની નિર્માણ એન્થાલ્પી અનુક્રમે $52, -394$ અને $-286\, KJ$ મોલ$^{-1}$ છે. $C_2H_4$ ની દહન એન્થાલ્પી.......$KJ \,mole^{-1}$View Solution
- 53$27\,^oC$ એ $10 $ મોલ ઓક્સિજન વાયુ ધરાવતા $5$ લીટર સીલીન્ડર છે. કારણ કે તે છિદ્ર નથી તુરંત જ લીક થાય છે. બધો જ વાયુ વાતાવરણમાં બહાર ફેલાય છે. અને સીલીન્ડર ખાલી થાય છે. જો વાતાવરણ દબાણ $1.0$ વાતાવરણ હોય તો વાયુ દ્વારા થતું કાર્ય કેટલું થશે ?View Solution
- 54$298 \,K$ તાપમાને $C - H, C - C, C = C$ અને $H - H$ ની બંધ-ઊર્જા અનુક્રમે $414, 347, 615$ અને $435$ કિલો જૂલ મોલ$^{-1}$ છે, તો ${H_2}C = C{H_{2(g)}} + {H_{2(g)}} \to {H_3}C - C{H_{3(g)}}$પ્રક્રિયા દરમિયાન $298\, K$ તાપમાને એન્થાલ્પી-ફેરફાર કેટલા .....કિલો જૂલ થશે ?View Solution
- 55$298\, K$ તાપમાને કાર્બન મોનોકસાઈડની પ્રમાણિત નિર્માણ ઉષ્મા ${-1}10.5\, kJ$ છે. તો $298 \,K$ અને અચળ કદે કાર્બન મોનોકસાઈડની પ્રમાણિત નિર્માણ ઉષ્મા ............... $\mathrm{kJ/mol}$છે.View Solution
- 56$298$ તાપમાને અચળ બાહ્ય દબાણ હેઠળ $ 2$ મોલ વાયુનું $5 \,dm^3$ થી $40 \,dm^3$ માં સમઉષ્મીય વિસ્તરણ પામે તો થયેલ કાર્ય અને પરિવર્તન માટે $W_{rev}$ .....,..... થશે.View Solution
- 57$300\,K$ એ $C_6H_5COOH_{(s}), CO_{2(g)}$ અને $H_2O_{(l)}$ ની પ્રમાણિત નિર્માણ એન્થાલ્પી અનુક્રમે $-408, -393$ અને $-286\, kJ \,mol^{-1}$ છે. તો અચળ કદે બેન્ઝોઈક એસિડની દહન ઉષ્મા કેટલા .....$kJ$ થાય ?$(R = 8.31 \,J \,mol^{-1}\,K^{-1})$View Solution
- 58$373 \,K $ એ એક મોલ પાણીનું વરાળમાં રૂપાંતરણ થાય છે. એક દબાણે $40.68\, kJ$ ઉષ્મા શોષાય છે. પાણી અને વરાળના મોલર કદ $18\, mL$ અને $30600 \,mL$ હોય તો પ્રક્રિયા માટે $\Delta U$ .........$kJ$ શોધો.View Solution
- 59$400\, mL$ $0.2\, M$ $H_2SO_4$ ને $600\, mL$ $0.1\, M$ $NaOH$ સાથે મિશ્ર કરવામાં આવે ત્યારે ઉત્પન્ન થતી ઉષ્માનો જથ્થો $3.43\, kJ$ છે. જો પાણીની વિશિષ્ટ ઉષ્મા $4.18\, J\, K^{-1}\,g^{-1}$ હોય, તો અંતિમ દ્રાવણના તાપમાનમાં થતો વધારો ...........$K$ થશે. (અંતિમ દ્રાવણની વિશિષ્ટ ઉષ્માક્ષમતા પાણી જેટલી ધારો)View Solution
- 60$600\, W$ પાવર ધરાવતા ઇલેક્ટ્રિક હીટર દ્વારા $80\, mL$ પાણીના બાષ્પીભવન માટે $8$ મિનિટનો સમય લાગે છે. તો પાણીની બાષ્પાયન એન્થાલ્પી .........$kJ\,mo{l^{ - 1}}$ થશે.View Solution
- 61$ 6C_{(s)} + 3H_2$ $\rightarrow C_6H_{6(l)} $ પ્રક્રિયામાં બેન્ઝીનની નિર્માણ ઉષ્મા કેટલા ......$JK$ થશે ?View Solution
બેન્ઝીનની દહન ઉષ્મા $-3268$, $CO_2$ ની નિર્માણ ઉષ્મા $-393.5$ અને $H_2O_{(l)}$ ની નિર્માણ ઉષ્મા $-285.8\, KJ$ છે.
- 62$A $ $\rightleftharpoons$ $ B$ પ્રક્રિયા માટે $log_{10}K$ નું મુલ્ય શોધો.આપેલ : $\Delta _fH^o_{298\,K} = -54.07\, kJ\, mole^{-1}, \Delta _rS^o_{298\,K} = 10\, J\,K^{-1}\,mol^{-1}, $View Solution
$R = 8.314\, J\,K^{-1}\,mol^{-1} \,\,\,2.303 \times 8.314 \times 298 = 5705$
- 63$C_6H_{12}O_6 + 6O_2 \rightarrow 6CO_2 + 6H_2O : \Delta H = -72$ કિલોકેલેરી હોય, તો $1.6$ ગ્રામ ગ્લુકોઝના નિર્માણ માટે ... કિલોકેલેરી ઊર્જા જરૂરી છે.View Solution
- 64$CO_2$$_{(g)}$, $H_2O_{(g)}$ અને $C_2H_4$ ની નિર્માણ એન્થાલ્પી અનુક્રમે $-393.7, -241.8, 52.3\, kJ$ પ્રતિ મોલ છે. તો $298\, K$ અને $1$ વાતા દબાણે $CO_2$, અને $H_2O$ ના નિર્માણ માટે ઈથીલીનની દહન એન્થાલ્પી કેટલા .....$JK ^{-1} \,mol ^{-1}$ થશે ?View Solution
- 65$C + O_2$ $\rightarrow$ $CO_2$ : $\Delta H = -395$ કિલોજૂલ, $S + O_2$ $\rightarrow$ $SO_2$ : $\Delta H = -295$ કિલોજૂલ, $CS_2 + 3O_2$ $\rightarrow$ $CO_2 + 2SO_2$ : $\Delta H = {-1}$$110$ કિલોજૂલ, તો $CS_2$ ની સર્જન ઉષ્મા......કિલોજૂલ/મોલView Solution
- 66$C + O_2$ $\rightarrow$ $CO_2$ : $\Delta H$ = $-x$ કિલોજૂલ, $2CO + O_2$ $\rightarrow$ $2CO_2$ : $\Delta H^° = -y$ કિલોજૂલ હોય, તો કાર્બન મોનેક્સાઈડની સર્જન એન્થાલ્પી (સર્જન ઉષ્મા) શોધો.View Solution
- 67$CO_2$ અને $H_2O$ ની નિર્માણ ઉષ્મા અનુક્રમે $-97 \,kcal$ અને $-68\, kcal $ છે. બેન્ઝિનની દહન ઉષ્મા $-783 \,kcal$ છે. તો બેન્ઝિનની નિર્માણ ઉષ્મા કેટલા .......$kcal$ ?View Solution
- 68$C$ ની દહન-ઉષ્મા $-x kJ$ પાણીની સર્જન-ઉષ્મા $-y kJ$ અને મિથેનની દહન-ઉષ્મા $ -z kJ$ હોય, તો મિથેનની સર્જન-ઉષ્મા કેટલી હશે ?View Solution
- 69$Fe + 1/2{O_2} \to FeO + x\,kcal$View Solution
$2Fe + 1/2{O_2} \to F{e_2}{O_3} + y\,kcal$ હોય, તો $Fe$ અને ઓક્સિજન માંથી$F{e_2}{O_3}$ ના સર્જનની ઉષ્મા ... થશે.
- 70$\frac{1}{2}{x_2} + \frac{3}{2}{y_2} \to x{y_3}$ પ્રક્રિયામાં $\Delta H = -30$ કિલોજૂલ/મોલ છે.View Solution
$\Delta {S_{({x_2})}}\,\, = \,\,60\,$ જૂલ/મોલ કેલ્વિન, $\Delta {S_{({y_2})}}\,\, = \,\,40$ જૂલ/મોલ કેલ્વિન $\Delta {S_{(x{y_3})}}\,\, = \,\,50\,$ જૂલ/મોલ કેલ્વિન
હોય, તો સંતુલને તાપમાને ......$K$
- 71$H_2 + Cl_2 \rightarrow 2HCl$ પ્રક્રિયામાં ઉષ્માનું ઉત્સર્જન થાય છે. $H - H$ અને $ Cl - Cl$ ની બંધ ઉર્જા અનુક્રમે $430$ અને $242$ $KJ/$મોલ છે. $H - Cl $ બંધ ઉર્જા.....$KJ\, mol^{-1}$View Solution
- 72$HgO$ માટે ${\Delta _f}{H^o}$ નુ મૂલ્ય $- 90.5\, kJ mol^{-1}$ છે. તો $1600\, kJ$ ઉષ્મા દ્વારા $HgO$ માંથી ઉષ્મીય રીતે ઉત્પન્ન થતા $Hg$ નો જથ્થો .........થશેView Solution
- 73${I_{2\left( s \right)}}$ ની ઊર્ધ્વીકરણ ઊર્જા $57.3\, kJ\, mol^{-1}$ અને ગલન એન્થાલ્પી $15.5\, kJ\,mol^{-1}$ છે. તો ${I_2}$ ની બાષ્પાયન એન્થાલ્પી .....................$kJ\,mo{l^{ - 1}}$ થશે.View Solution
- 74$S + \frac{3}{2}{O_2}\, \to \,S{O_3} + 2x\,$ કિલોકેલેરી $\Delta H\,\, = \,\, - y$ કિલોકેલેરી, $S{O_2} + \frac{1}{2}{O_2} \to S{O_3} + y$ કિલોકેલેરી $\Delta H = -2x$ કિલોકેલરી, તો $SO_2$ ની સર્જન ઉષ્મા $= ......$View Solution
- 75$X_2$, $Y_2$ અને $XY_3$ ના પ્રમાણિત એન્ટ્રોપી અનુક્રમે $60, 40$ અને $50 $ $J\,K^{-1}$ $mol^{-1}$ છે. તો, $\frac{1}{2}{X_2}\, + \,\,\frac{3}{2}{Y_2}\, \to \,X{Y_3},\,\Delta H\,\, = \,\, - 30\,\,kJ,$ પ્રક્રિયાના સંતુલન વખતે કેટલા ......$K$ તાપમાન હશે ?View Solution
- 76$X \,gm$ ઈથેનાલ $(CH_3CHO)$ ને બોમ્બ કેલેરીમીટરમાં સળગાવે છે અને $Y$ જુલ ઉષ્મા ઉત્પન્ન થાય છે. તો .....View Solution
- 77અચળ કદે નેપ્થેલીન $(C_{10}H_8$$_{(s)})$ ની દહન ઉષ્મા $-5133 \,KJ \,mol^{-1}$ છે. તો એન્થાલ્પી ફેરફારનું મૂલ્ય ....$J$ $( R = 8.314\, J\,K^{-1} \,mol^{-1}).$View Solution
- 78ઇથિલિનના ચોક્કસ જથ્થાનું દહન કરતા $6226\, kJ$ ઉષ્મા ઉત્પન્ન થાય છે. જો તેની દહન-એન્થાલ્પી $1411\, kJ\, mol^{-1}$ હોય, તો $STP$ એ પ્રક્રિયામાં વપરાયેલા ઓક્સિજન પરમાણુઓની સંખ્યા ...............${N_A}$ થશે.View Solution
- 79એક મોલ આદર્શવાયુ કે જેના માટે $C_v = (3/2)\,R$ છે તેને $1\,atm$. ના અચળ દબાણે $25\,^oC$ થી $100\,^oC$ તાપમાને ગરમ કરવામાં આવે છે. તો $\Delta H$......$cal$ થશે.View Solution
- 80એક વાયુ $1\,atm$. ના અચળ દબાણે $10\, dm^3$ માંથી $20\, dm^3$ કદમાં સમતાપી વિસ્તરણ પામે છે. જો તે પર્યાવરણમાંથી $800\, J$ ઉષ્મીય ઊર્જાનુ શોષણ કરે તો આ પ્રકમ માટે $\Delta U$ કેટલા .....$J$ થશે?View Solution
- 81એસીટીલીનની નિર્માણ ઉષ્મા .....$KJ$ માં શોધો.View Solution
$2 \mathrm{C}_{(\mathrm{s})}+2 \mathrm{O}_2(\mathrm{~g}) 2 \mathrm{CO}_2(\mathrm{~g}), \Delta \mathrm{H}=-787 \mathrm{KJ} ; \mathrm{H}_2(\mathrm{~g})+$$\mathrm{H}_2 \mathrm{O}, \Delta \mathrm{H}=-286 \mathrm{KJ}$
$\frac{1}{2} \mathrm{O}_2 \mathrm{C}_2 \mathrm{H}_2(g)+\frac{5}{2} \mathrm{O}_2(g) \rightarrow 2 \mathrm{CO}_2(g)+\mathrm{H}_2 \mathrm{O}(I), \Delta H=-1310KJ$
- 82View Solutionકઈ ઉષ્માક્ષેપક પ્રક્રિયા છે ?
- 83કાલ્પનીક પ્રતિવર્તીં પ્રક્રિયા $\frac{1}{2} A_{2(g)} + \frac{3}{2} B_{2(g)}$ $\rightarrow AB_{3(g)}$; $\Delta H = -20 \,KJ$ માટે જો $A_2, B_2 $અને $AB_3$ નું પ્રમાણિત એન્ટ્રોપી અનુક્રમે $60, 40$ અને $50$ $JK^{-1}$ મોલ$^{-1}$ છે. તો .....$K$ તાપમાને ઉપરની પ્રક્રિયાનું સંતુલન થાય છે?View Solution
- 84કુદરતી વાયુ ધારો કે જે મિથેન અને ઈથેનનું એક માત્ર મિશ્રણ છે. $S.T.P.$ એ $10$ લીટર વાયુનું સંપૂર્ણ દહન કરતાં ઉત્પન્] થતી ઉષ્મા $476.6 \,kJ$ છે. $\Delta H_{comb}$ $CH_4$$_{(g)} = -894\, kJ \,mol$ અને $\Delta H_{comb}$ $C_2H_6 = {-1} 500\, kJ \,/ mol$ તો કદ દ્વારા મિશ્રણ ઘટકો મિથેન અને ઈથેન ની ટકાવારી ..... થશે.View Solution
- 85કોઈ એક પ્રક્રિયા માટે $\Delta H = + 3\,kJ$ અને $\Delta S = + 10\,J/K$ છે. તો ......$K$ લઘુત્તમ તાપમાન કરતા ઊંચા તાપમાને પ્રક્રિયા સ્વયંભૂ થશે ?View Solution
- 86કોલમ$-I$ ના રૂપાંતરણને કોલમ$-II$ માં આપેલ યોગ્ય વિકલ્પ સાથે જોડો.View Solution
કોલમ$-I$ કોલમ$-II$
$(A)\;CO_2(s)\;\to\;CO_2(g)$
$(p)$ સંક્રાંતિ માધ્યમ
$(B)\;CaCO_3(s)\;to\;CaO(s)$
$+ CO_2(g)$
$(q)$ અપરરૂપ ફેરફાર
$(C)\;2H^{\cdot}\;\to\;H_2(g)$
$(r)\;\Delta\, H \,\frac{1}{2}$ ધન છે.
$(D)\;P$ (સફેદ ધન) $\to\;P$( વાવ ધન)
$(s)\;\Delta\,S \,\frac{1}{2}$ ધન છે.
$(t)\;\Delta\, S$ ઋણ છે.
- 87જો $N_2O$ ની સર્જન-એન્થાલ્પી $82\, kJ\, mol^{-1}$ હોય તો $N_2O$ ની સંસ્પંદન ઊર્જા ગણો.......$kJ\,mo{l^{ - 1}}$View Solution
$N \equiv N\,\left( {946\,kJ\,mo{l^{ - 1}}} \right)\,;\,N = N\,\left( {418\,kJ\,mo{l^{ - 1}}} \right)$
$O = O\,\left( {498\,kJ\,mo{l^{ - 1}}} \right)\,;\,N = O\,\left( {607\,kJ\,mo{l^{ - 1}}} \right)$;
- 88જો અચળ કદે આઇસોબ્યુટેનની દહન-ઉષ્મા $R$ (વાયુ અચળાંક) હોય, તો અચળ દબાણે પ્રમાણિત સ્થિતિમાં એક મોલ છે આઇસોબ્યુટેનના દહનની ઉષ્મા કેટલી થશે ?View Solution
- 89જો કોઈ પદાર્થ માટે ગલનબિંદુ $T_B$ તથા ઠારબિંદુ $T_A$ હોય તો એન્ટ્રોપીમાં થતા ફેરફાર અને તાપમાન વચ્ચેનો સાચો સંબંધ કયા આલેખ વડે દર્શાવી શકાય ?View Solution
- 90જો તેના પરમાણુમાંથી બનતા $NH_3$ ની પ્રમાણિત નિર્માણ એન્થાલ્પી $-46.0\, kJ \,mol ^{-1}$ છે. $H_2$ ની નિર્માણ એન્થાલ્પી $-436\, kJ \,mol ^{-1}$ હોય અને $N_2$ ની $-712 \,kJ\, mol$$^{-1}$ હોય તો $NH_3$ માં $N - H $ બંધની સરેરાશ બંધ એન્થાલ્પી કેટલા .......$kJ \,mol^{-1}$ થશે ?View Solution
- 91જ્યારે $2$ મોલ $C_2H_{6(g)}$ સંપૂર્ણ સળગે ત્યારે $3129\, kJ$ ઉષ્મા છૂટી પાડે છે. $C_2H_{6(g)}$ ની નિર્માણ ઉષ્મા કેટલી થશે ?View Solution
$CO_{2(g)}$ અને $H_2O$ ના $\Delta H_f$ અનુક્રમે $-395$ અને $ -286$ $kJ \,mol^{-1}$ છે........$KJ$
- 92જ્યારે $2$ મોલ $C_2H_6$ સંપૂર્ણ પણે સળગી $3129\, kJ$ ઉષ્મા છૂટી પાડે છે. તો $C_2H_6$ ની નિર્માણ ઉષ્મા .....$J$ થશે. $CO_2$ અને $H_2O$ ની $\Delta \,Hf$ અનુક્રમે $-395$ અને $-286 \,kJ$ છે.View Solution
- 93જ્યારે $300$ કેલ્વિને $63.50$ ગ્રામ ઝીંકને હાઈડ્રોક્લોરિક એસીડનાં ખૂલ્લા બીકરમાં દ્રાવ્ય કરવામાં આવે તો થતાં કાર્યની ગણતરી .....$J$ થશે. $(Zn$ નો પરમાણુભાર $= 63.5 \,amu)$View Solution
- 94જ્યારે $6.80 \,g$ $NH_3$ ને ગરમ $CuO $ પરથી પસાર કરવામાં આવે તો એન્થાલ્પીનો ફેરફાર કેટલો થાય $?$ અહિ $NH_3$ $_{(g)}$, $CuO$$_{(s)}$ અને $H_2O$$_{(l)}$ ની પ્રમાણિત એન્થાલ્પી ઉષ્મા અનુક્રમે $-46.0$, $55.0$ અને $-285.0\, kJ\, mol$ $^{-1}$ છે. અને પ્રક્રિયા,View Solution
$N{H_{3(g)}}\, + \,\,\frac{3}{2}\,Cu{O_{(s)}}\, \to \,\,\frac{1}{2}\,{N_{2(g)}}\, + \,\,\frac{3}{2}{H_2}{O_{(\ell )}}\, + \,\,\frac{3}{2}\,C{u_{(s)}}.$ ......$J$
- 95ધારો કે રાંધણ ગેસનો સિલિન્ડરમાં $11.2\,kg$ આઈસોબ્યુટેન ધરાવે છે. તો બ્યુટેનના દહન માટેનું ઉષ્મા રાસાયણિક સમીકરણ નીચે આપેલ છે.View Solution
${C_4}{H_{10}}_{(g)}\,\, + \,\,\frac{{13}}{2}\,{O_2}_{(g)}\,\, \to \,\,4C{O_2}_{(g)}\,\, + \,\,5{H_2}O(\ell )\,\,\,\,\,\,\,;$
$\,\,\,\,\,\,\Delta H\,\, = \,\, - 2658\,\,KJ$
જો પરિવારને દરરોજ રાંધવા માટે $15000\,KJ$ ઊર્જા જરૂર પડે. તો સીલીન્ડર ......દિવસ સુધી ચાલશે ?
- 96નિર્જળ ઓકઝેલિક એસિડની દહન એન્થાલ્પી $x\,kcal\, mol^{-1}$ હોય, તો $2\, g$ ઓકઝેલિક એસિડના દહનથી ઉત્પન્ન થતી ઉષ્મા કેટલા કિલોકેલરી થશે ?View Solution
- 97નીચે આપેલ પરિબળો દ્વારા જલીય દ્રાવણમાં ક્લોરીનની ઓક્સિડાઈઝ ક્ષમતા માપી શકાય છે. તો $1/2 Cl_2$$_{(g)}$ થી $Cl^{-}$ $_{(aq)}$માં રૂપાંતરણ થવા કેટલા .....$kJ\, mol^{-1}$ ઉર્જા ભાગ લેશે ?View Solution
$\frac{1}{2}C{l_2}_{(g)}\,\xrightarrow{{\frac{1}{2}{\Delta _{diss}}{H^\Theta }}}\,Cl_{(g)}\,\,\xrightarrow{{{\Delta _{eg}}{H^\Theta }}}\,\,C{l^ - }_{(g)}\,\xrightarrow{{{\Delta _{hyd}}{H^\Theta }}}\,C{l^ - }_{(aq)}$
$({\mkern 1mu} {\Delta _{diss}}{\mkern 1mu} H_{C{l_2}}^\Theta {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} 240{\mkern 1mu} {\mkern 1mu} kJ{\mkern 1mu} {\mkern 1mu} mo{l^{ - 1}},{\mkern 1mu} {\mkern 1mu} {\Delta _{eg}}{\mkern 1mu} H_{Cl}^\Theta {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} - 349{\mkern 1mu} {\mkern 1mu} kJ{\mkern 1mu} {\mkern 1mu} mo{l^{ - 1}},{\mkern 1mu} {\mkern 1mu} $
${\Delta _{hyd}}H_{C{l^ - }}^\Theta {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} - {\mkern 1mu} 381{\mkern 1mu} kJ{\mkern 1mu} {\mkern 1mu} mo{l^{ - 1}})$
- 98નીચે આપેલ માહિતી પરથી $OH^-$ આયનની સર્જન-ઉષ્માની કીમત $252\,^oC$ તાપમાને.....$KJ$ શોધો.View Solution
${H_2}{O_{(l)}} \to \,\,H_{(aq)}^ + + \,\,OH_{(aq)}^ - \,;\,\,\,\Delta H\,\, = \,\,57.32\,\,KJ\,;$
${H_2}_{(g)} + \,\,\frac{1}{2}\,\,{O_2}_{(g)} \to \,\,{H_2}{O_{(1)}}\,;\,\,\Delta H\,\, = \,\, - 286.20\,\,KJ$
- 99નીચે દર્શાવેલ પ્રક્રિયાને આધારે $ICl_{(g)}$ ની પ્રમાણિત સર્જનએન્થાલ્પી ગણો. આયોડિન અને ક્લોરિનની પ્રમાણિત સ્થિતિ અનુક્રમે $I_2$ $_{(s)}$ અને $Cl_2$$_{(s)}$ છે.View Solution
$(i)$ $Cl_2$$_{(g)}$ $=$ $2Cl_{(g)}$ , $\Delta H = 242.3$ કિલો જૂલ મોલ$^{-1}$
$(ii)$ $I_2$$_{(g)}$ $=$ $2I_{(g)}$, $\Delta H = 151.0$ કિલો જૂલ મોલ$^{-1}$
$(iii)$ $ICl_{(g)}$ $=$ $I_{(g)} +$ $Cl_{(g)}$, $\Delta H = 211.3$ કિલો જૂલ મોલ$^{-1}$
$(iv)$ $I_{2(s)}$ $=$ $I_{2(g)}$, $\Delta H = 62.76$ કિલો જૂલ મોલ$^{-1}$
.....કિલો જૂલ મોલ$^{-1}$
- 100નીચેના પૈકી કઈ પ્રક્રિયામાં $\Delta$ $S$ મહત્તમ છે ?View Solution