Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1View Solutionवृत्त की ________ उसकी त्रिज्या के साथ स्थिर अनुपात होता है।
- 2View Solutionपहिए द्वारा एक चक्कर में तय की गइ दूरी भ्रमण करते हुए पहिए के ________ बराबर है।
- 3View Solutionघूर्ण करते हुए पहिए द्वारा पूर्ण किए गए घूर्णनों की संख्या एक मिनट में = एक मिनट में तय दूरी / ________.
- 4$4$ सेमी. त्रिज्या तथा कोण $30^o$ वाले सैक्टर का क्षेत्रफल $\pi$ के पदों में $....$ है।View Solution
- 5View Solutionवृत्त का ________ परिधि से घिरा होता है।
- 6View Solutionएक वृत्त की परिधि = ________.
- 7एक घड़ी की मिनट की सुई जिसकी लंबाई $14 \ cm$ है। इस सुई द्वारा $5$ मिनट में रचित क्षेत्रफल ज्ञात कीजिए। $(\pi=\frac{22}{7})$View Solution
- 8एक वृत्त के चतुर्थांश $($quadrant$)$ का क्षेत्रफल ज्ञात कीजिए, जिसकी परिधि $22 \ cm$ है।View Solution
- 9त्रिज्या $R$ वाले वृत्त के उस त्रिज्यखंड का क्षेत्रफल जिसका कोण $p^\circ$ है, निम्नलिखित है$:$View Solution
- 10जहाज़ों को समुद्र में जलस्तर के नीचे स्थित चट्टानों की चेतावनी देने के लिए, एक लाइट हाउस $($ light house $)\ 80^\circ$ कोण वाले एक त्रिज्यखंड में $16.5 \ km$ की दूरी तक लाल रंग का प्रकाश फैलाता है। समुद्र के उस भाग का क्षेत्रफल ज्ञात कीजिए जिसमें जहाज़ों को चेतावनी दी जा सके। $(\pi = 314$ का पयोग कीजिए$)$View Solution
- 11किसी कार के दो वाइपर $($Wipers$)$ हैं, परस्पर कभी आच्छादित नहीं होते हैं। प्रत्येक वाइपर की पत्ती की लंबाई $25 \ cm$ है और $115^\circ$ के कोण तक घूम कर सफाई कर सकता है। पत्तियों की प्रत्येक बुहार के साथ जितना क्षेत्रफल साफ हो जाता है, वह ज्ञात कीजिए। $(\pi = \frac{22}{7})$View Solution
- 12एक छतरी में आठ ताने हैं, जो बराबर दूरी पर लगे हुए हैं। छतरी को $45 \ cm$ त्रिज्या वाला एक सपाट वृत्त मानते हुए, इसकी दो क्रमागत तानों के बीच का क्षेत्रफल ज्ञात कीजिए।View Solution
- 13$6 \ cm$ त्रिज्या वाले एक वृत्त के एक त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण $60^\circ$ है। $(\pi = \frac{22}{7})$View Solution
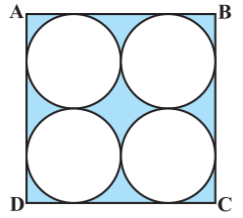
- 14आकृति में छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए, जहाँ $\text{ABCD}$ भुजा $14 \ cm$ का एक वर्ग है।View Solution
- 15त्रिज्या $4 \ cm$ वाले एक वृत्त के त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण $30^\circ$ है। साथ ही, संगत दीर्घ त्रिज्यखंड का क्षेत्रफल भी ज्ञात कीजिए। $(\pi = 3.14$ का प्रयोग कीजिए$)$।View Solution
- 16एक वृत्ताकार खेत पर $₹24$ प्रति मीटर की दर से बाड़ लगाने का व्यय $₹5280$ है। इस खेत की $₹0.50$ प्रति वर्ग मीटर की दर से जुताई कराई जानी है। खेत की जुताई कराने का व्यय ज्ञात कीजिए। $(\pi = \frac{22}{7}$ लीजिए$)$।View Solution
- 17एक वृत्ताकार ब्रूच $($brooch$)$ को चाँदी के तार से बनाया जाना है जिसका व्यास $35\ mm$ है। तार को वृत के $5$ व्यासों को बनाने में भी प्रयुक्त किया गया है जो उसे $10$ बराबर त्रिज्यखंडों में विभाजित करता है जैसा कि आकृति में दर्शाया गया है। तो ज्ञात कीजिए:View Solution
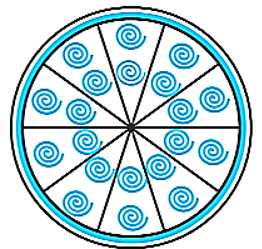
- कुल वांछित चाँदी के तार की लंबाई
- ब्रूच के प्रत्येक त्रिज्यखंड का क्षेत्रफल
- 18$15 m$ भुजा वाले एक वर्गाकार घास के मैदान के एक कोने पर लगे खूँटे से एक घोड़े को $5 m$ लंबी रस्सी से बाँध दिया गया है। ज्ञात कीजिए:View Solution
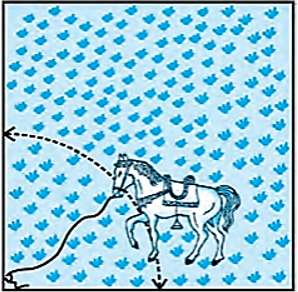
- मैदान के उस भाग का क्षेत्रफल जहाँ घोड़ा घास चर सकता है।
- चरे जा सकने वाले क्षेत्रफल में वृद्धि, यदि घोड़े को $5 m$ लंबी रस्सी के स्थान पर $10 m$ लंबी रस्सी से बाँध दिया जाए। $(\pi = 3.14$ का प्रयोग कीजिए।$)$
- 19त्रिज्या $12 \ cm$ वाले एक वृत्त की कोई जीवा केंद्र पर $120^\circ$ का कोण अंतरित करती है। संगत वृत्तखंड का क्षेत्रफल ज्ञात कीजिए। $(\pi = 3.14$ और $\sqrt{3} = 1.73$ का प्रयोग कीजिए$।)$View Solution
- 20$15 \ cm$ त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर $60^\circ$ का कोण अंतरित करती है। संगत लघु और दीर्घ वृत्तखंडों के क्षेत्रफल ज्ञात कीजिए। $(\pi = 3.14$ और $\sqrt{3} = 1.73$ का प्रयोग कीजिए$।)$View Solution
- 21त्रिज्या $21 \ cm$ वाले वृत्त का एक चाप केंद्र पर $60^\circ$ का कोण अंतरित करता है। ज्ञात कीजिए:View Solution
- चाप की लंबाई
- चाप द्वारा बनाए गए त्रिज्यखंड का क्षेत्रफल
- संगत जीवा द्वारा बनाए गए वृत्तखंड का क्षेत्रफल $(\pi=\frac{22}{7})$
- 22$10$ सेमी त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर एक समकोण अंतरित करती है। निम्नलिखित के क्षेत्रफल ज्ञात कीजिए :View Solution
- संगत लघु वृत्तखंड
- संगत दीर्घ त्रिज्यखंड $(\pi = 3.14$ का प्रयोग कीजिए$)।$
- 23एक गोल मेज़पोश पर छ: समान डिज़ाइन बने हुए हैं जैसाकि आकृति में दर्शाया गया है। यदि मेज़पोश की त्रिज्या $28 \ cm$ है, तो $₹0.35$ प्रति वर्ग सेंटीमीटर की दर से इन डिज़ाइनों को बनाने की लागत ज्ञात कीजिए। $(\sqrt{3} = 1.7$ का प्रयोग कीजिए$)$View Solution
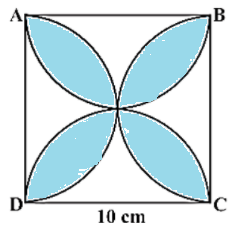
- 24आकृति में, छायांकित डिज़ाइन का क्षेत्रफल ज्ञात कीजिए, जहाँ $\text{ABCD}$ भुजा $10 \ cm$ का एक वर्ग है तथा इस वर्ग की प्रत्येक भुजा को व्यास मान कर अर्धवृत्त खींचे गए हैं। $(\pi = 3.14$ का प्रयोग कीजिए।$)$View Solution
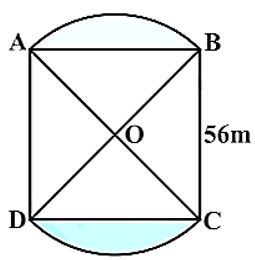
- 25आकृति में, $56 m$ भुजा वाले एक वर्गाकार लॉन $($lawn$) \text{ABCD}$ के दो ओर बनी हुई दो वृत्ताकार फूलों की क्यारियाँ दर्शाई गई हैं। यदि प्रत्येक वृत्ताकार क्यारी का केंद्र लॉन के विकर्णों का प्रतिच्छेद बिंदु $O$ है, तो वर्गाकार लॉन तथा फूलों की क्यारियों के क्षेत्रफलों का योग ज्ञात कीजिए। $(\pi = \frac{22}{7}$ का प्रयोग कीजिए$)$।View Solution
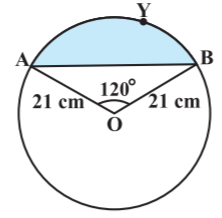
- 26आकृति में दर्शाए गए वृत्तखंड का क्षेत्रफल ज्ञात कीजिए, यदि वृत्त की त्रिज्या $21 \ cm$ है और $\angle AOB = 120^\circ$ है। $[\pi = \frac{22}{7}$ लीजिए$]$View Solution
- 27View Solutionकिमी आयत को उसकी भुजा के परितः घुमाने से निर्मित आकृति क्या होगी?
- 28View Solutionयदि किसी धन का सम्पूर्ण पृष्ठ 24 वर्ग सेमी है, तो उसकी प्रत्येक कोर की लम्बाई क्या होगी?
- 29View Solutionएक धन की कोर सेमी है, तो धन का पतन क्या होगा?
- 30View Solutionएक मन के विवर्णकी लम्बाई 15 सेमी है। चमकी बोरी माप क्या होगी?
- 31View Solutionएकमसीकोरोंकी संख्या होती क्या है?
- 32View Solutionएकवर्गाकार कमरे का आयतन 100 घन मीटर है। यदि उसकी ऊंचाई 4 मीटर है, तो उसकी लम्बाई क्या होगी?
- 33View Solutionएक घनाभ की तीन कोरें 3 सेमी, 4 सेमी और 5.5 सेमी है। पनाम का आयतन क्या होगा?
- 34View Solutionएक घनाकार ठोस का आयतन 27 घन सेमी है। उस ठोस का सम्पूर्ण पष्ठ क्या होगा?
- 35View Solutionएक घनाम की कोरें 3 सेमी, 4 सेमी और 8 सेमी हैं, तो उसका सम्पूर्ण पृष्ठ क्या होगा?
- 36View Solutionएक पनाम की कोरें क्रमशः 3 सेमी, 4 सेमी तथा 12 सेमी है। पनाम के.विकर्ण की लम्बाई क्या होगी?
- 37किसी पत्तीय बेलनाकार पात्र मी ऊँचाई = $10 \mathrm{m}$ ओर आधार-त्रिज्या = $7 \mathrm{cm}$ है, तो उस पात्र की धारिता क्या हैView Solution
- 38एक धन का माधत्तम $125 \mathrm{m}^{3}$ है, तो जसका कुल पछ-क्षेत्रफल क्या होगा?View Solution
- 39View Solutionसमबेलम का पूर्ण पक-क्षेत्रपाल क्या होता है
- 40View Solutionएक पनाम के तीन मलम पालकों के क्षेत्रफल ओर वर्ग स्काई। उसका आयतन क्रम बाई बराबर होगा?
- 41एक खोखले गोले के बाहरी व्यास तथा भीतरी व्यास क्रमशः $\mathrm{x}$ और $\mathrm{y}$ तो खोखले गोले के डोम भाग का आयतन निम्नलिखित में कोन-सा होगा?View Solution
- 42View Solutionकिसी शंकुके आधार की त्रिज्या और ऊँचाई समान है। उसके आयतन और उसी त्रिज्या वाले एक गोले के आयतन का अनुपात क्या होगा?
- 43View Solutionकिसी गोले के पष्ठ-क्षेत्रफल और उसी त्रिज्या के एक अर्बगोले के कुल पष्ठतल का अनुपात क्या है?
- 44View Solution2a cm किनारे वाले धन का आयतन औरam आधार-त्रिज्या एवं a cm ऊँचाई वाले शंकु के आयतन का अनुपात क्या होगा
- 45किमी लंबपत्तीय शंकु की आधार-त्रिज्या = $\mathrm{r} \mathrm{cm}$ और ऊँचाई = $\mathrm{h} \mathrm{cm}$ है, तो शंकु का कुल पृष्ठ-क्षेत्रफल क्या होगा।View Solution
- 46View Solutionबराबर आयतन एवं आधार के वृत्ताकार समवेलन एवं लंबवत्तीय शंक की ऊँचाइयों का अनुपात क्या है?
- 47View Solution2.1 cm त्रिज्या तथा 8.4 cm ऊँचाई वाले शंकु को पिघलाकर एक ठोस गोला बनाया गया तो गोले की त्रिज्या क्या होगी?
- 48किसी बेलन के आधार का व्यास $4 \mathrm{cm}$ तथा ऊँचाई $14 \mathrm{cm}$ है तो बेलन का आयतन क्या होगा?View Solution
- 49View Solutionr त्रिज्या एवं। तिर्यक ऊँचाई वाले शंकु का पूर्ण पृष्ठ क्षेत्रफल क्या है?
- 50View Solutionसमान आधार और समान ऊँचाई वाले बेलन तथा अर्द्धगोले के आयतन का अनुपात क्या है?
- 51$7 \mathrm{cm}$ त्रिज्या वाले अर्धगोले का कुल पृष्ठीय क्षेत्रफलView Solution
- 52खोखले गोलीय शेल का बाहरी व्यास एवं भीतरी व्यास क्रमशः $x$ तथा $\mathrm{y}$ है तो इसका आवतन क्या होगा?View Solution
- 53यदि घनाभ की लम्बाई, चोड़ाई तथा ऊँचाई क्रमश: $12 \mathrm{cm}, 10 \mathrm{cm}$ तथा $8 \mathrm{cm}$ हो तो घनाभ का आयतन क्या होगा?View Solution
- 54View Solutionसमान ऊँचाई वाले दो लंबवत्तीय बेलनों के आयतनों का अनुपात 9 : 16 है तो उनकी त्रिज्याओं का अनुपात क्या होगा ?
- 55View Solutionयदि गोले की त्रिज्या आधी कर दी जाए तो मूल गोले और नये गोले के आयतनों का अनुपात क्या होगा ?
- 56$\mathrm{r}$ त्रिज्या तथा $\mathrm{h}$ ऊँचाई वाले बेलन का आयतन क्या है ?View Solution
- 57यदि शंकु के निक के सिरों की त्रिज्याएं क्रमशः $\mathrm{R}$ एवं $\mathrm{r}$ तथा h छिन्रक की ऊर्ध्वाधर ऊँचाई हो तो छिन्रक का आयतन क्या होगाView Solution
- 58View Solutionr त्रिज्या वाले अडंगोले का आयतन है
- 59$\mathrm{r}$ त्रिज्या बाले गोले का आयतन क्या है?View Solution
- 60यदि अबंगोले की त्रिज्या $r$ हो तो उसका सम्पूर्ण पृष्ठ क्षेत्रफल क्या होगा?View Solution
- 61View Solution10 m किनारे वाले धन को पिघलाकर 2 cm किनारे वाले किसने बन बनाए जा सकते है?
- 62View Solutionकिसी घन के एक किनारा और विकर्ण की लम्बाई का अनुपात क्या है
- 63View Solutionसमान आधार और समान उचाई वाले लघवत्तीय बेलन और लंबवत्तीय शंकु के आयतनों का अनुपात कितना होगा?
- 64View Solutionयदि शंकु के आधार का क्षेत्रफल उसके आयतन के बराबर हो तो शंकु की ऊँचाई क्या होगी?
- 65View Solution14 cm ऊँचाई वाले बेलन का आयतन 11 सेमी किनारे वाले घन के आयतन के बराबर है तो बेलन का व्यास क्या है
- 66घनाभ के तीन संलग्र फलकों का क्षेत्रफल क्रमशः $\mathrm{x}^{2}, \mathrm{y}^{2}$ तथा $\mathrm{z}^{2}$ है तो इसका आयतन बराबर होगा।View Solution
- 67यदि घन की एक भुजा a $\mathrm{cm}$ हो तो विकर्ण की लम्बाई होगीView Solution
- 68यदि धन का आयतन $125 \mathrm{cm}^{3}$ हो तो घन का पृष्ठ क्षेत्रफल क्या होगा?View Solution
- 69View Solutionएक लम्बवृत्तीय शंकु जिसकी ऊँचाई 15 सेमी. तथा आयतन 125 घन सेमी. है तो इसकी त्रिज्या क्या होगी?
- 70View Solutionनिम्रलिखित में से बेलन का आयतन निकालने का सूत्र क्या है जबकि उसके आधार की त्रिज्या r ऊँचाई है?
- 71त्रिज्या $\mathrm{R}$ वाले वृत्त के उस त्रित्यखंड का क्षेत्रफल जिसका कोण $\mathrm{P}^{\circ}$ है, निम्नलिखित में कोन हे?View Solution
- 72View Solutionकिसी लम्ब वृत्तीय शंकु के पूर्ण पृष्ठ का क्षेत्रफल होगा जहाँ, r त्रिज्या, । तिर्यक ऊँचाई, h ऊँचाई हो
- 73एक अर्द्रगोले का आयतन 19404$^{3}$सेमी है, तो अर्द्रगोले का कुल पृष्ष क्षेत्रफल क्या हे?View Solution
- 74View Solutionएक अर्द्धगोले के त्रिज्या 6.3 cm है। इसका पूर्णपृष्ठीय क्षेत्रफल क्या होगा?
- 75View Solutionकिसी बाल्टी की ऊँचाई 24 सेमी. है तथा त्रिज्याएँ 5 सेमी. एवं 15 सेमी. हैं। बाल्टी का पृष्ठीय क्षेत्रफल क्या होगा?
- 76यदि वर्ग का विकर्ण $16 \sqrt{2}$ सेमी. है, तो दन को शुजा की लम्बाई होगीView Solution
- 77View Solutionपानी का आयतन बतावें यदि किसी 40 m ऊँची बाल्टी के वृत्तीय सिरों की त्रिज्याएँ 35 cm तथा 14 cm है तो
- 78View Solution'r' त्रिज्या के गोले का आयतन क्या होता है
- 79यदि किसी अर्द्रगोलाकार पात्र की त्रिज्या $\mathrm{k} \mathrm{cm}$ है, तो उसका आयतन कितना होगा?View Solution
- 80View Solutionएक घनाभ की लम्बाई, चौड़ाई एवं ऊँचाई क्रमश: 12, 10, 8 मी. है। इसका पृष्ठीय क्षेत्रफल क्या होगा?
- 81गोला के सम्पूर्ण पृष्ठ का क्षेत्रफल निम्न में कौन होगा अगर त्रिज्या = $r$ होView Solution
- 82View Solutionयदि घन का आयतन 216 cm3 हो तो धन का किनारा कितना होगा?
- 83View Solutionअधेगोले के सम्पूर्ण सतह का क्षेत्रफल क्या होता है
- 84View Solutionएक बाल्टी की ऊँचाई 45 सेमी. तथा छोर की त्रिज्याएँ 28 सेमी. तथा 7 सेमी. हैं, तो बाल्टी की क्षमता क्या होगी?
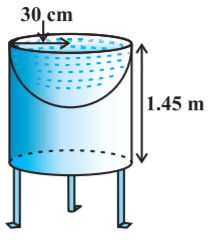
- 85मयंक ने अपने बगीचे के लिए एक पक्षी$-$स्नानागार $($bird$-$bath$)$ बनाया जिसका आकार एक खोखले बेलन जैसा है जिसके एक सिरे पर अर्धगोलाकार बर्तन बना हुआ है $($देखिए आकृति$)$। बेलन की ऊँचाई $1.45 m$ है और उसकी त्रिज्या $30 \ cm$ है। इस पक्षी$-$स्नानागार का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।View Solution
- 86एक घनाकार ब्लॉक के एक फलक को अंदर की ओर से काट कर एक अर्धगोलाकार गड्ढा इस प्रकार बनाया गया है कि अर्धगोले का व्यास घन के एक किनारे के बराबर है। शेष बचे ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए। $(\pi=\frac{22}{7})$View Solution
- 87भुजा $7 \ cm$ वाले एक घनाकार ब्लॉक के ऊपर एक अर्धगोला रखा हुआ है। अर्धगोले का अधिकतम व्यास क्या हो सकता है? इस प्रकार बने ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए। $(\pi=\frac{22}{7})$View Solution
- 88एक खिलौना त्रिज्या $3.5 \ cm$ वाले एक शंकु के आकार का है, जो उसी त्रिज्या वाले एक अर्धगोले पर अध्यारोपित है। इस खिलौने की संपूर्ण ऊँचाई $15.5 \ cm$ है। इस खिलौने का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।View Solution
- 89कोई बर्तन एक खोखले अर्धगोले के आकार का है जिसके ऊपर एक खोखला बेलन अध्यारोपित है। अर्धगोले का व्यास $14 \ cm$ है और इस बर्तन $($पात्र$)$ की कुल ऊँचाई $13 \ cm$ है। इस बर्तन का आंतरिक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।View Solution
- 90दो घनों, जिनमें से प्रत्येक का आयतन $64 \ cm^3$ है, के संलग्न फलकों को मिलाकर एक ठोस बनाया जाता है। इससे प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए। $(\pi=\frac{22}{7})$View Solution
- 91सेल्वी के घर की छत पर बेलन के आकार की एक टंकी है। इस टंकी में एक भूमिगत टंकी में भरे पानी को पंप द्वारा पहुँचा कर टंकी को भरा जाता है। यह भूमिगत टंकी एक घनाभ के आकार की है, जिसकी विमाएँ $1.57 m \times 1.44 m \times 95 \ cm$ हैं। छत की टंकी की त्रिज्या $60 \ cm$ है और ऊँचाई $95 \ cm $ है। यदि भूमिगत टंकी पानी से पूरी भरी हुई थी, तो उससे छत की टंकी को पूरा भरने के बाद भूमिगत टंकी में पानी कितनी ऊँचाई तक रह जाएगा? छत की टंकी की धारिता की भूमिगत टंकी की धारिता से तुलना कीजिए। $(\pi = 3.14$ लीजिए।$)$View Solution
- 92मॉडल बनाने वाली मिट्टी से ऊँचाई $24 \ cm$ और आधार त्रिज्या $6 \ cm$ वाला एक शंकु बनाया गया है। एक बच्चे ने इसे गोले के आकार में बदल दिया। गोले की त्रिज्या ज्ञात कीजिए।View Solution
- 93एक ठोस खिलौना एक अर्धगोले के आकार का है जिस पर एक लंब वृत्तीय शंकु आरोपित है। इस शंकु की ऊँचाई $2 \ cm$ है और आधार का व्यास $4 \ cm$ है। इस खिलौने का आयतन निर्धारित कीजिए। यदि एक लंब वृत्तीय बेलन इस खिलौने के परिगत हो तो बेलन और खिलौने के आयतनों का अंतर ज्ञात कीजिए। $(\pi = 3.14$ लीजिए।$)$View Solution
- 94एक जूस $($juice$)$ बेचने वाला अपने ग्राहकों को आकृति में दर्शाए गिलासों से जूस देता था। बेलनाकार गिलास का आंतरिक व्यास $5 \ cm$ था, परंतु गिलास के निचले आधार $($तली$)$ में एक उभरा हुआ अर्धगोला था, जिससे गिलास की धारिता कम हो जाती थी। यदि एक गिलास की ऊँचाई $10 \ cm$ थी, तो गिलास की आभासी $($apparent$)$ धारिता तथा उसकी वास्तविक धारिता ज्ञात कीजिए। $(\pi = 3.14$ लीजिए।$)$View Solution
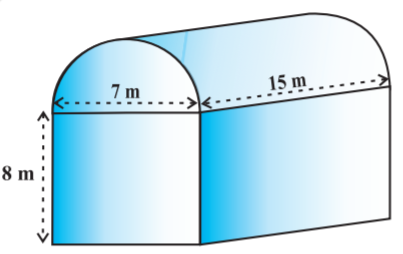
- 95शांता किसी शेड $($shed$)$ में एक उद्योग चलाती है। यह शेड एक घनाभ के आकार का है जिस पर एक अर्धबेलन आरोपित है $($देखिए आकृति$)$। यदि इस शेड के आधार की विमाएँ $7 m \times 15 m$ हैं तथा घनाभाकार भाग की ऊँचाई $8 m$ है तो शेड में समावेशित हो सकने वाली हवा का आयतन ज्ञात कीजिए। पुन: यदि यह मान लें कि शेड में रखी मशीनरी $300 m^3$ स्थान घेरती है तथा शेड के अंदर $20$ श्रमिक हैं जिनमें से प्रत्येक $0.08 m^3$ के औसत से स्थान घेरता है तब शेड में कितनी हवा होगी?$ (\pi=\frac{22}{7}$ लीजिए$।)$View Solution
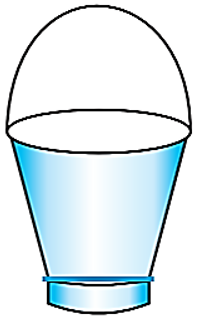
- 96धातु से बनी एक खुली बाल्टी शंकु के एक छिन्नक के आकार की है, जो उसी धातु के बने एक खोखले बेलनाकार आधार पर आरोपित है $($देखिए आकृति$)$। इस बाल्टी के दोनों वृत्ताकार सिरों के व्यास $45 \ cm$ और $25 \ cm$ हैं तथा बाल्टी की कुल ऊर्ध्वाधर ऊँचाई $40 \ cm$ और बेलनाकार आधार की ऊँचाई $6 \ cm$ है। इस बाल्टी को बनाने में प्रयुक्त धातु की चादर का क्षेत्रफल ज्ञात कीजिए जबकि हम बाल्टी की मुठिया $($या हत्थे$)$ को इसमें सम्मिलित नहीं कर रहे हैं। साथ ही, उस पानी का आयतन ज्ञात कीजिए जो इस बाल्टी में धारण कर सकता है। $\pi=\frac{22}{7}$ लीजिएView Solution
- 97हनुमप्पा और उसकी पत्नी गंगाम्मा गन्ने के रस से गुड़ बना रहे हैं। उन्होंने गन्ने के रस को गर्म करके राब $($शीरा$)$ बना ली है, जिसे शंकु के छिन्नक के आकार के साँचों में डाला जाता है, जिनमें से प्रत्येक के दोनों वृत्तीय फलकों के व्यास क्रमशः $30 \ cm $ और $35 \ cm$ हैं तथा साँचे की ऊर्ध्वाधर ऊँचाई $14 \ cm$ है $($देखिए आकृति$)$। यदि $1 \ cm^3$ राब का द्रव्यमान लगभग $1.2 g$ है तो प्रत्येक साँचे में भरी जा सकने वाली राब का द्रव्यमान ज्ञात करें। $\pi=\frac{22}{7}$ लीजिएView Solution

- 98एक शंकु के छिन्नक, जो $45 \ cm$ ऊँचा है, के सिरों की त्रिज्याएँ $28 \ cm$ और $7 \ cm$ हैं। इसका आयतन, वक्र पृष्ठीय क्षेत्रफल और संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए। $(\pi=\frac{22}{7}$ लीजिए$)$View Solution
- 99पानी से पूरी भरी हुई एक अर्धगोलाकार टंकी को एक पाइप द्वारा $3 \frac{4}{7}$ लीटर प्रति सेकंड की दर से खाली किया जाता है। यदि टंकी का व्यास $3 m$ है, तो वह कितने समय में आधी खाली हो जाएगी? $(\pi = \frac{22}{7}$ लीजिए।$)$View Solution
- 100व्यास $1 \ cm$ वाली $8 \ cm$ लंबी ताँबे की एक छड़ को एकसमान मोटाई वाले $18 m$ लंबे एक तार के रूप में खींचा जाता $($बदला जाता$)$ है। तार की मोटाई ज्ञात कीजिए।View Solution