Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1$298$ $K$ પર આપેલ અર્ધ કોપ માટે પોટેન્શિયલ (-)_________ $\times 10^{-2} \mathrm{~V}$ છે.View Solution
$2 \mathrm{H}_{(\mathrm{aq})}^{+}+2 \mathrm{e}^{-} \rightarrow \mathrm{H}_2(\mathrm{~g})$
${\left[\mathrm{H}^{+}\right]=1 \mathrm{M}, \mathrm{P}_{\mathrm{H}_2}=2 \mathrm{~atm}}$
(Given: $2.303 \mathrm{RT} / \mathrm{F}=0.06 \mathrm{~V}, \log 2=0.3$ )
- 2આયનોના રિડકશન પોટેન્શિયલ નીચે આપેલા છે.View Solution
$ClO_4^{-}$ $IO_4^{-}$ $BrO_4^{-}$ $E^{\circ}=1.19 V$ $E^{\circ}=1.65 V$ $E^{\circ}=1.74 V$ તેમની ઓક્સિડાઈઝીંગ સામર્શ્ય (ક્ષમતા) નો સાચો ક્રમ શોધો.
- 3કઈ ધાતુઓ બેટરી ઉદ્યોગોમાં ઉપયોગી છે.View Solution
$A$. $\mathrm{Fe}$ $B$. $\mathrm{Mn}$ $C$. $\mathrm{Ni}$ $D$. $\mathrm{Cr}$ $E$. $\mathrm{Cd}$
Choose the correct answer from the options given below:
- 4કોપર સલ્ફેટ માંથી $x \times 10^{-1}$ ગ્રામ પરમાણુ કોપર મેળવવા $1F$ વિદ્યુતપ્રવાહ જરૂરી છે. તો $x$ શોધો.View Solution
- 5ગોલ્ડ (સોનાના) ઈલેક્ટ્રોડો વચ્ચે $\mathrm{AuCl}_4^{-}$આયનના દ્રાવણમાંથી અચળ વિદ્યુત પ્રવાહ (કરંટ) પસાર કરવામાં આવ્યો. $10$ મિનીટના સમય બાદ (પછી) કેથોડના દળ (વજન)માં $1.314 \mathrm{~g}$ વધારો હતો. દ્રાવણમાંથી પસાર કરેલ કૂલ ભાર._______$\times 10^{-2} \mathrm{~F}$ હતો. (આપેલ $\mathrm{Au}$ નું પરમાણ્વીય દળ = $197$)View Solution
- 6View Solutionનીચે આપેલ ક્યું પરિબળ દ્રાવણુની વિદ્યુતીય વાહકતાને અસર કરતું નથી.
- 7નીચે આપેલ રેડોક્ષ પ્રક્રિયાને ધ્યાનમાં લો.View Solution
$\mathrm{MnO}_4^{-}+\mathrm{H}^{+}+\mathrm{H}_2 \mathrm{C}_2 \mathrm{O}_4 \rightleftharpoons \mathrm{Mn}^{2+}+\mathrm{H}_2 \mathrm{O}+\mathrm{CO}_2$
પ્રમાણિત રિડકશન પોટેન્શિયલ નીચે આપેલા છે. $\left(\mathrm{E}_{\mathrm{red}}^{\circ}\right)$
$\mathrm{E}_{\mathrm{MmO}_4^{-} / \mathrm{Mm}^{2+}}^{\circ}=+1.51 \mathrm{~V}$
$\mathrm{E}_{\mathrm{CO}_2 / \mathrm{H}_2 \mathrm{C}_2 \mathrm{O}_4}^{\circ}=-0.49 \mathrm{~V}$
જો ઉપરની પ્રક્રિયાને સંતુલન અચળાંક $K_{e q}=10^x$, તરીકે આપેલ હોય તો, $x$ નું મૂલ્ય = ___________. (નજીકનો પૂણુાંક)
- 8View Solutionલોખંડ (આયર્ન) નું કટાવવું (કાટ લાગવો) ના સંદર્ભમાં નીચે આપેલા વિધાનોમાંથી ક્યું સાચું નથી?
- 9વિદ્યૃતના જથ્થા (માત્રા) દ્વારા (વડે) વિસ્થાપિત સિલ્વર ($Ag$ નું મોલર દળ $108 \mathrm{gmol}^{-1}$ ) નું દળ કે જે $S.T.P.$ પર $\mathrm{O}_2$ ના $5600\ mL$ ને વિસ્થાપિત કરશે તે __________$g$ થશે.View Solution
- 10$0.001\,mm$ જાડાઈના નિકલ સ્તરનું $100\,cm ^2$ વિસ્તારના એક ધાતુનું કટિંગ (થર) કરવામાં આવ્યું. ઇચ્છિત સ્તરનું થર (કોટ) ચઢાવવા માટે $Ni \left( NO _3\right)_2$ના દ્રાવણમાથી $2A$ નો પ્રવાહ એ '$x$' સેકન્ડો માટે પસાર કરવામાં આવ્યો. તો $x$ નું મૂલ્ય $.......$ છે.(નજીકનો પૂર્ણાક) ( $\rho_{ Ni }$ (નિકલની ધનતા) એે $10\,g\,mL ^{-1}$ છે.નિકલનું મોલર દળ $60\,g\,mol ^{-1}$ છે.$\left( F =96500\,C\,mol ^{-1}\right)$View Solution
- 11$1 \times 10^{-5}\,M \textrm {AgNO } _ { 3 }$ ને $AgBr$ના $1\,L$ સંતૃપ્ત દ્રાવણમાં ઉમેરવામાં આવે છે.$298\,K$ આ દ્રાવણની વાહકતા $.........\times 10^{-8}\,S\,m ^{-1}$ છે.View Solution
$\left[\right.$ આપેલ : $K _{ sp }( AgBr )=4.9 \times 10^{-13}$ at $298 K$
$\lambda_{ Ag ^{+}}^0=6 \times 10^{-3} Sm ^2\,mol ^{-1}$
$\lambda_{ Br ^{-}}^0=8 \times 10^{-3} Sm ^2\,mol ^{-1}$
$\left.\lambda_{ NO _3^{-}}^0=7 \times 10^{-3} Sm ^2\,mol ^{-1}\right]$
- 12$298\,K$ એ પ્રક્રિયા,View Solution
$Zn ( s )+ Sn ^{2+}$ (જલીય) $\rightleftharpoons Zn ^{2+}$ જલીય $+ Sn ( s )$ ની સંતુલન અચળાંક $1 \times 10^{20}$ છે. તો $Sn / Sn ^{2+}$ વિદ્યુત ધ્રુવની (ઈલેકટ્રોડ પોટેન્શિયલ) માત્રા જો $E_{Z n}^0 2+/ Zn =-0.76 V$ માટે $..............\times 10^{-2}\,V$ છે. (નજીકના પૂર્ણાંકમાં)
આપેલું છે: $\frac{2.303 RT }{ F }=0.059\,V$
- 13$298\,K$ પર $10\,mmol Cr _2 O _7^{2-}$ અને $100\,mmol\,Cr ^{3+}$ ધરાવતું દ્રાવણ એ $3\,pH$ દર્શાવે છે. આપેલ : $Cr _2 O _7^{2-} \rightarrow Cr ^{3+} ; E ^0=1.330\,V$ અને $\frac{2.303 RT }{ F }=0.059\,V$ અર્ધ કોષ પ્રક્રિયા માટે નો પોટેન્શિયલ $x \times 10^{-3}\,V$ છે. તો $x$ નું મૂલ્ય $..........$ છે.View Solution
- 14$298\,K$ પર નીચે આપેલા કોષનો કોષ પોટેન્શિયલ $X \left| X ^{2+}(0.001 M ) \| Y ^{2+}(0.01 M )\right| Y$ એ $..............\times 10^{-2}\,v$ છે.View Solution
આપેલ: $E _{ x ^{2+} \mid x }^0=-2.36\,V$
$E _{ Y ^{3+} \mid Y }^0=+0.36\,V$
$\frac{2.303\,RT }{ F }=0.06\,V$
- 15$\frac{1}{2} H _2( g )+ AgCl ( s ) \rightleftharpoons H ^{+}( aq )+ Cl ^{-}( aq )+ Ag ( s )$ પ્રક્રિયા એ આપેલ કયા ગેલ્વોનિક કોષ માં થાય છે ?View Solution
- 16$Pd ^{2+}+4 Cl ^{-} \rightleftharpoons PdCl _4^{2-}$ પ્રક્રિયા માટે સંતુલન અચળાંકનો લધુગણક $...........$ (નજીકનો પૂર્ણાંક)View Solution
આપેલ $: \frac{2.303 RT }{ F }=0.06 V$
$Pd _{( aq )}^{2+}+2 e ^{-} \rightleftharpoons Pd ( s ) \quad E ^{\circ}=0.83\,V$
$PdCl _4^{2-}( aq )+2 e ^{-} \rightleftharpoons Pd ( s )+4 Cl ^{-}( aq )$
$E ^{\circ}=0.65\,V$
- 17એક નિશ્ચિત તાપમાન $0.0025\,M$ એસિટિક એસિડ ની વિશિષ્ટ વાહકતા $5 \times 10^{-5}\,S\,cm ^{-1}$ છે.એસિટિક એસિડનો વિયોજન અચળાંક $......\times 10^{-7}$ છે. (નજીકનો પૂર્ણાક) ( $CH _3 COOH$ ની સિમીત મોલર વાહક્તા $400\,S\,cm ^2\, mol ^{-1}$ તરીકે ધ્યાનમાં લો,)View Solution
- 18એક વિદ્યુતવિભાજ્ય ના $0.8\,M$ દ્વાવણની પ્રતિરોધકતા $5 \times 10^{-3}\,\Omega\,cm$ છે.તો તેની મોલર વાહકતા $.......\times 10^4\, \Omega^{-1}\,cm ^2\,mol ^{-1}$ છે.View Solution
- 19કોષને ધ્યાનમાં લો:View Solution
$Pt ( s )\left| H _2( s )( latm )\right| H ^{+}\left( aq ,\left[ H ^{+}\right]=1\right)|| Fe ^{3+}( aq ), Fe ^{2+}( aq ) \mid \operatorname{Pt}( s )$
આપેલ : $E _{ Fe ^{3+} / e ^{2 *}}^0=0.771\,V$ અને $E _{ H ^{+}+\frac{1}{2} H _2}^0=0\,V , T =298\,K$
જો કોષનો પોટેન્શિયલ $0.712\,V$, હોય, તો $Fe ^{-2}$ થી $Fe ^{+3}$ ની સાંદ્રતાની ગુણોત્તર છે.(નજીકનો પૂર્ણાંક)
- 20લેડની વિદ્યુતરાસાયણિક પ્રક્રિયામાં, પ્રમાણિત તાપમાન પર, જો $E ^{\circ}\left( Pb ^{2+} / Pb \right)= m$ volt અને $E ^0\left( Pb ^{4+} / Pb \right)= n$ volt, તો પછી $E ^0\left( Pb ^{2+} / Pb ^{4+}\right)$ નું મૂલ્ય એ $m - xn$ વડે આપવામાં આવે છે. તો x નું મૂલ્ય $..........$ છે.View Solution
- 21લેડ સંગ્રાહક બેટરી માટે સાચા વિધાનો શોધો.View Solution
$A$. બેટરીના ચર્જિંગ દરમિયાન,એનોડ ઉપરનો $PbSO _4 PbO _2$ માં પરિવર્તિત થાય છે.
$B$. બેટરીના ચર્જિંગ દરમિયાન, કેથોડ ઉપરનો $PbSO _4 PbO _2$ માં પરિવર્તિત થાય છે.
$C$. લેડ સંગ્રાહક બેટરી એનોડ તરીકે $PbO _2$ સાથે ભરેલ લેડની ગ્રીડ ધરાવે છે.
$D$. લેડ સંગ્રાહક બેટરી એક વિદ્યુતવિભાજય તરીકે $38\%$ સલ્ફ્યુરિક એસિડ નું દ્રાવણ ધરાવે છે.
નીચે આપેલા વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો.
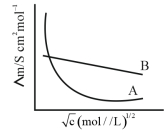
- 22સાંદ્રતા પર બે વિદ્યુતવિભાજ્યોની મોલર વાહકતા નો આધાર $(dependence)$ નીચે આકૃતિમાં દર્શાવેલ છે.$\Lambda \stackrel{\circ}{m}$ એ સિમિત મોલર વાહક્તા છે.View Solution
નીચે આપેલા માંથી ખોટા વિધાન(નો)ની સંખ્યા $..........$ છે.
$(A)$ $\Lambda \stackrel{0}{ m }$ for electrolyte $A$ is obtained by extrapolation
$(B)$ વિદ્યુતવિભાજ્ય $B$ માટે $\Lambda m$ વિરૂદ્ધ $\sqrt{c}$ આલેખ સીધી રેખા મળે છે અને સાથે આંતરછેદ એ $\Lambda \stackrel{0}{ m }$ ને બરાબર (સમાન) છે.
$(C)$ અનંત મંદન પર વિદ્યુતવિભાજ્ય $B$ માટે વિયોજન અંશ નું મૂલ્ય શૂન્ય પ્રસ્થાપિત કરે છે.
$(D)$ વિદ્યુતવિભાજ્ય $A$ અથવા $B$ માટે $\Lambda \stackrel{0}{ m }$ વ્યક્તિગત આયનો માટે $\lambda^{\circ}$ નો ઉપયોગ કરીને ગણતરી કરી શકાય છે ?
- 23$298\,K$ પર, $Cu ^{2+} / Cu$ ઈલેકટ્રોડ માટે પ્રમાણિત રિડકશન પોટેન્શિયલ $0.34\,V$ છે.આપેલ : $K _{ sp } Cu ( OH )_2=1 \times 10^{-20}$ $\operatorname{Take} \frac{2.303 RT }{ F }=0.059 \,V$ લો.ઉપરના કપલ (યુગ્મ) માટે $pH =14$ પર રિડકશન પોટેન્શિયલ $(-) x \times 10^{-2}\,V$ છે.$x$નું મુલ્ય $........$ છે.View Solution
- 24$FeO _4^{2-} \stackrel{+2.2\,V }{\longrightarrow} Fe ^{3+} \stackrel{+0.70\,V }{\longrightarrow} Fe ^{2+} \stackrel{-0.45\,V }{\longrightarrow} Fe ^0$View Solution
$E _{ FeO _4^{2-} / Fe ^{2+}}^\theta$ એ $x \times 10^{-3} V$. તો $x$ નું મૂલ્ય $.........$.છે.
- 25$Pt ( s ) H _2( g )(1 bar )\left| H ^{+}( aq )(1 M )\right|\left| M ^{3+}( aq ), M ^{+}( aq )\right| Pt ( s )$View Solution
$298\,K$ પર જ્યારે $\frac{\left[M^*(a q)\right]}{\left[M^{3 *}(a q)\right]}=10^a$ હોય ત્યારે આપેલ કોષ નો $E_{\text {cell }}$ એ $0.1115\,V$ છે. $a$ નું મૂલ્ય $............$ છે.આપેલ : $E _{ M }^\theta{ }^{3+} M ^{+}=0.2\,V$
$\frac{2.303\,R T}{F}=0.059\,V$
- 26$V, Cr, Mn,$ અને $Co$ માટે પ્રમાણિત ઈલેકટ્રોડ $\left( M ^{3+} / M ^{2+}\right)$ અનુક્રમે $-0.26\,V ,-0.41\,V ,-0.57\,V$ અને $+1.97\,V$ છે. ધાતુ આયનો કે જે મંદ એસિડ માંથી $H _2$ મૂક્ત કરે છે તે શોધો.View Solution
- 27કોષને ધ્યાનમાં લોView Solution
$Pt _{( s )}\left| H _2( g , 1\,atm )\right| H ^{+}( aq , 1 M )|| Fe ^{3+}( aq ), Fe ^{2+}( aq ) \mid Pt ( s )$
$298\,K$ પર જયારે કોષ નો પોટેન્શિયલ $0.712\,V$ હોય તો $\left[ Fe ^{2+}\right] /\left[ Fe ^{3+}\right]$ નો ગુણોત્તર $.......$ છે.
આપેલ:$Fe ^{3+}+ e ^{-}= Fe ^{2+}, E ^{\circ} Fe ^{3+}, Fe ^{2+} \mid Pt =0.771$
$\frac{2.303 RT }{ F }=0.06\,V$
- 28નીચે આપેલામાંથી ખોટા વિધાનોની સંખ્યા $........$ છે.View Solution
$A$. વિદ્યૃતકાર્ય કે જે પ્રક્રિયા અચળ દબાણ અને તાપમાન પર કરી શકે છે.તે પ્રક્રિયા ગિબ્સ ઊર્જા જેટલી છે.
$B$. $E ^{\circ}$ કોષ એ દબાણ ઉપર આધારિત છે.
$C$. $\frac{d E^\theta \text { cell }}{ dT }=\frac{\Delta_{ r } S ^\theta}{ nF }$
$D$. પોટેન્શિયલ તફાવતના વિરોધી સ્રોત દ્વારા જો કોષ પોટેન્શિયલ બરાબર સંતુલિત હોય તો કોષ ઊલટાવી શકાય તેવું કાર્ય કરે છે.
- 29નીચે આપેલા માંથી સાયા વિધાનોની સંખ્યા $.......$ છે.View Solution
$A$. $E$ કોષ એક માત્રાત્મક માપદંડ છે.
$B$. ઋણ $E ^\theta$ નો અર્થ એ થાય છે કે રેડોક્ષ કપલ એ $H ^{+} / H _2$ કપલ કરતાં વધારે પ્રબળ રિડકશનકર્તા છે.
$C$. અોકસીડેશન અથવા રીડકશન માટે જરૂરી વિદ્યુત પ્રવાહનો જથ્થો ઈલેકટ્રોડ પ્રક્રિયાના તત્વયોગમિતિય પર આધાર રાખે છે.
$D$. વિદ્યુતપ્રવાહ દ્વારા વિદ્યુત વિભાજન દરમિયાન કોઈ પણ ઇલેકટ્રોડ પર થતી રસાયણિક પ્રક્રિયાની માત્ર વિદ્યુતવિભાજય દ્વારા પસાર થતા વિદ્યુતપ્રવાહના જથ્થાના સમપ્રમાણમાં હોય છે.
- 30$1\, mol$ $Cr _{2} O _{7}^{2-}$ $Cr ^{3+}$ નું રીડક્શન કરવા જરૂરી વિદ્યુતનો જથ્થો ફેરાડેમાં $\dots\dots$ છે.View Solution
- 31$20\, mL\, NaCl$ના $10\, moles$ દ્રાવણ સાથે ભરેલ વાહકતા કોષની મોલર વાહકતા $\Lambda_{ m 1} $ છે અને $80\, mL\, NaCl$ના $20\, moles$ દ્રાવણની $\Lambda_{ m 2}$ છે. બંને કોષો વડે પ્રદર્શિત થતી વાહકતા સમાન છે. $\Lambda_{ m 2}$ અને $\Lambda_{ m 1}$ વચ્ચેનો સંબંધ શોધો.View Solution
- 32$298\,K$ એ $0.01\,M\,KCl$ દ્રાવણ ધરાવતા વાહકતા કોષનો અવરોધ $1750\,\Omega$ છે. $0.01M$ $KCl$ દ્રાવણની $298 K$ એ વાહકતા $0.152 \times 10^{-3}\,S\,cm ^{-1}$ છે. તો આ વાહકતા કોષની કોષ અચળાંક $\dots\dots\times 10^{-3} cm ^{-1}$.View Solution
- 33$298\, K$ એ $Zn \left| Zn ^{2+}( aq ) \| Sn ^{x+}\right| Sn$ નો કોષ પોટેન્શિયલ $0.801 \,V$ છે. આ પ્રક્રિયાનુ પ્રક્રિયા ભાગફળ $10^{-2}$ છે. આપેલ વિદ્યુત રાસાયણિક કોષ પ્રક્રિયામાં સંકળાયેલ ઈલેક્ટ્રોનોની સંખ્યા $....$ છે.View Solution
(આપેલ : $E _{ Zn ^{2+} \mid Zn }^{ o }=-0.763 V , E _{ Sn ^{x+} \mid Sn }^{ O }=+0.008 V$ ધારી લો $\frac{2.303 RT }{ F }=0.06\, V$ )
- 34$298\,K$ એ કોષ આપેલ પ્રક્રિયા માટે પોટેન્શિયલView Solution
$Pt \left| H _{2}( g , 1 bar )\right| H ^{*}( aq ) \| Cu ^{2+}( aq ) \mid Cu ( s )$
$0.31\,V$ છે. આ એસિડિક દ્રાવણની $pH$ માલુમ પડી. જ્યારે $Cu ^{2+}$ નું સાંદ્રતા $10^{-x} m$ છે.તો $x$ નું મૂલ્ય $\dots\dots$.
(આપેલ: $E _{ Cu ^{2+} / Cu }^{\ominus}=0.34 \,V$ અને $\left.\frac{2.303 RT }{ F }=0.06\, V \right)$
- 35$NaI, NaNO _{3}$ અને $AgNO _{3}$ ની સિમિત મોલર વાહકતાઓ (limiting molar conductivities) અનુક્રમે $12.7,12.0$ અને $13.3\, mS m { }^{2}\, mol ^{-1}$ છે. (બધા $25^{\circ} C$ તાપમાને). તો આ જ તાપમાને $AgI$ ની સિમિત મોલર વાહકતા $......\,mS m ^{2}\, mol ^{-1}$ છેView Solution
- 36$Pt \left| H _{2}( g )\right| H ^{+}( aq ) \| Cu ^{2+}(0.01 M ) \mid Cu ( s )$View Solution
$298\,K$ પર આપેલ કોષ માટે કોષ પોટેન્શિયલ $0.576\,V$ છે. દ્રાવણની $pH\dots\dots\dots$ છે.(નજીકનો પૂર્ણાંક)
(આપેલ : $E _{ Cu ^{2+} / Cu }=0.34\,V$ અને ધરી લો $\frac{2.303\,RT }{ F }=0.06\,V$ )
- 37આપેલ પ્રક્રિયાઓ માટેView Solution
$Sn ^{2+}+2 e ^{-} \rightarrow Sn$
$Sn ^{4+}+4 e ^{-} \rightarrow Sn$
ઈલેક્ટ્રોન (વિદ્યુતધ્રુવ) પોટેન્શિયલ ની $E _{ Sn ^{2+} / Sn }^{\circ}=-0.140 V$ અને $E _{ Sn ^{4+} / Sn }^{\circ}=0.010 V$ છે. $Sn ^{4+} / Sn ^{2+}$
$E^{o} _{ Sn ^{4+} / Sn ^{2+}}$માટે પ્રમાણિત ઈલેક્ટ્રોડ (વિદ્યુતધ્રુવ) પોંટેન્શિયલની માત્રા........ $\times 10^{-2} V$ છે. (નજીકનો પૂર્ણાક)
- 38એક કોષ માટે, $Cu ( s ) \mid Cu ^{2+}\left(0.001 M || Ag ^{+}(0.01\,M ) \mid Ag ( s )\right.$View Solution
કોષ પોટિન્શયયલ $298 \,K$ એ $0.43\, V$ માલુમ પડ્યો, તો પ્રમાણિત ઇલેકટ્રોડ પોટિન્શયયલની માત્રા $Cu ^{2+} / Cu$ માટે $........\times 10^{-2} \,V \vartheta$ છે.
$[$ આપેલ છે $:E _{ Ag ^{+} / Ag }^{\Theta}=0.80\, V \text { and } \frac{2.303 \,RT }{ F }=0.06\,V ]$
- 39નીચે બે વિધાનો આપેલા છે :View Solution
વિધાન $I :\,KI$ માટે, મંદન સાથે મોલર વાહકતામાં વધારો સીધો થાય છે.
વિધાન $II :$ કાર્બોનીક એસિડ માટે, મંદન સાથે મોલર વાહકતામાં વધારે ધીમો થાય છે.
ઉપરના વિધાનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સૌથી વધુ બંધબેસતો જવાબ પસંદ કરો.
- 40સૂચિ - $I$ સાથે સૂચિ - $II$ ને જોડો.View Solution
સૂચિ - $I$ સૂચિ - $II$ $(A)$ $Cd ( s )+2 Ni ( OH )_{3}( s ) \rightarrow CdO ( s )+2 Ni ( OH )_{2}( s )+ H _{2} O (l)$ $(I)$ પ્રાથમિક બેટરી $(B)$ $Zn ( Hg )+ HgO ( s ) \rightarrow ZnO ( s )+ Hg (l)$ $(II)$ દ્વિતિયક બેટરી (કોષ) નું ડિસચાર્જિંગ $(C)$ $2 PbSO _{4}( s )+2 H _{2} O (l) \rightarrow Pb ( s )+ PbO _{2}( s )+ 2 H _{2} SO _{4}( aq )$ $(III)$ બળતણા (ઈંઘણ) કોષ $(D)$ $2 H _{2}( g )+ O _{2}( g ) \quad \rightarrow 2 H _{2} O (l)$ $(IV)$ દ્વિતિયક બેટરીનું ચાર્જિંગ - 41$Fe _{2}\left( SO _{4}\right)_{3}$ નું દ્રાવણ $1.5\,A$ના પ્રવાહ સાથે $'X'\,min$. માટે તેનું વિદ્યુતવિભાજન કરતાં $0.3482\,g\,Fe$ જમા થાય છે. $x$ નું મૂલ્ય $\dots\dots\dots\,\min$ છે. [નજીકનો પૂર્ણાંક]View Solution
[આપેલ : $1\,F =96500\,C\,mol ^{-1},$ $Fe$નું પરમાણ્વીય દળ $= 56\,g\,mol ^{-1}$ ]
- 42$Fe _3 O _4$ માંથી આયર્નના એક મોલ મેળવવા માટે જરૂરી ભારની માત્રા $F$ માં $....$ છે. (નજીકનો પૂર્ણાંક)View Solution
- 43એક કોષમાં, નીચે આપેલ પ્રક્રિયાઓ ભાગ લે છે.View Solution
$Fe ^{2+} \rightarrow Fe ^{3+} + e ^{-} \quad E _{ Fe ^{3+} / Fe ^{2+}}=0.77 \,V$
$2 I ^{-} \rightarrow I _{2}+2 e ^{-} \quad E _{ I _{2} / I ^{-}}^{0}=0.54 \,V$
$298\,K$ પર, કોષ માં સ્વયંભૂ પ્રક્રિયા (આપમેળે પ્રક્રિયા) માટે પ્રમાણિત ઈલેક્ટ્રોડ પોટન્શિયલ $x \times 10^{-2}\,V$ છે.તો $x$ નું મૂલ્ય $\dots\dots\dots$ છે.(નજીકનો પૂર્ણાંક)
- 44નીચે આપેલ યુગ્મોનો રિડક્ષન પોટેન્શિયલનો સાચો ક્રમ શોધો.View Solution
$A.$ $Cl _{2} / Cl^{-}$ $B.$ $I _{2} / I^{-}$ $C.$ $Ag ^{+} / Ag$ $D.$ $Na ^{+} / Na$ $E.$ $Li ^{+} / Li$
નીચે આપેલામાંથી સાચો વિકલ્પ પસંદ કરો.
- 45$74.5 \,ppm\, KCl$ ના દ્રાવણ ભરેલા વાહક્તા કોષ (કોષ અચળાંક $129\, m ^{-1}$ )નો અવરોધ $100 \,\Omega$ (દ્રાવણ $1$ તરીકે લેબલ) છે. જ્યારે તે જ કોષ (સમાન કોષ) $149\, ppm \,KCl$ ના દ્રાવણ સાથે ભરેલું હોય તેનો અવરોધ $50 \,\Omega$ ( દ્રાવણ $2$ તરીકે લેબલ) છે. દ્રાવણ $1$ અને દ્રાવણ $2$ની મોલર વાહકતાઓનો ગુણોત્તર $i.e.\,\frac{\wedge_1}{\wedge_2}=x \times 10^{-3}$ છે, તો $x$નું મૂલ્ય $.....$ છે. (નજીકનો પૂર્ણાંક)View Solution
[આપેલ, $KCl$ નું મોલર દળ $74.5 \,g\, mol ^{-1}$ છે.]
- 46આપેલ $:E _{ Cu ^{2} / Cu }=0.34\, V ; E _{ Sn ^{2} / Sn }^{\ominus}=-0.14 \,V$View Solution
$298\,K$ પર પ્રક્રિયા માટે ગિબ્સ મૂક્ત ઊર્જા ફેરફાર $Cu ( s )+ Sn ^{2+}(0.001 \,M ) \rightarrow\,Cu ^{2+}(0.01 M )+ Sn ( s ), x \times 10^{-1}\, kJ \,mol ^{-1} s .$
[આપેલ : $F =96500\,C\,mol ^{-1}$ ] તો $x$ નું મૂલ્ય $\dots\dots$ છે.
- 47જુદા-જુદા પ્રકારના અર્ધ કોષોનો $\left(\frac{\partial E }{\partial T }\right)_{ P }$ નીચે મુજબ છે.View Solution
$\text { A } \quad\quad\quad\quad\quad \text { B } \quad\quad\quad\text { C } \quad\quad\quad\quad\text { D }$
$1 \times 10^{-4} \quad 2 \times 10^{-4} \quad 0.1 \times 10^{-4} \quad 0.2 \times 10^{-4}$
(અહિયાં,$E$ એ ઇલેક્ટ્રોમોટીવ બળ છે.)
ઉપર આપેલા અર્ધકોષો માંથી ક્યાનો સંદર્ભ ઈલેક્ટ્રોડ તરીકેનો ઉપયોગ પસંદગીય પામશે ?
- 48સલ્ફ્યુરિક એસિડના મંદ દ્રાવણનું $2$ કલાકો માટે તેમજ $0.10\,A$ પ્રવાહનો ઉપયોગ કરીને વિદ્યુત વિભાજન કરતા હાઈડ્રોજન અને ઓક્સિજન વાયુ ઉત્પન્ન થાય છે. $STP$ પર ઉત્પન્ન થતા વાયું નું કુલ કદ $......\,cm ^{3}$ છે. (નજીકનો પૂર્ણાંક)View Solution
[આપેલ : ફેરાડે અચળાંક $F =96500\,C\,mol ^{-1}$ $STP$ પર, આદર્શ વાયુ નું મોલર કદ $22.7\,L\,mol ^{-1}$ છે. ]
- 49$25^{\circ} C$ પર જો $H ^{+}$ આયનની સાંદ્રતા $1\, M$ થી $10^{-4} \,M$ માં ઘટેલ હોય તો $MnO _{4}^{-} / Mn ^{2+}$ જોડીમાં ઓક્સિડાઈઝીંગ પાવર (શક્તિ) માં ફેરફારની માત્રા $x \times 10^{-4} \,V$ છે. (ધારી લો કે $H ^{+}$ ની સાંદ્રતા માં ફેરબદલ થતા $MnO _{4}^{-}$ અને $Mn ^{2+}$ ની સાંદ્રતા સમાન રહે છે) તો $x$ નું મૂલ્ય ..... છે.View Solution
(નજીકના પૂર્ણાંકમાં રાઉન્ડ ઑફ કરો) $[$ આપેલ $\left.: \frac{2.303 RT }{ F }=0.059\right]$
- 50$298 \,K$ પર નીચે આપેલા કોષનો $Emf\, V$ માં $x \times 10^{-2}$ છે. તો $x$ નું મૂલ્ય .... છે. (નજીકના પૂર્ણાંકમાં રાઉન્ડ ઑફ)View Solution
$Zn | Zn ^{2+}(0.1\, M ) \| Ag ^{+}(0.01 \,M )| Ag$
[આપેલ $: E_{Z n^{+2}/Z_{n}}^{0}=-0.76 \,V ; E _{A g^{+} / A_{ g }}^{0}=+0.80 \,V ; \frac{2.303 RT }{ F }=0.059$]
- 51View Solutionએસિડિફાઇડ સલ્ફેટ દ્રાવણના વિદ્યુતવિભાજય ઓક્સિડેશનમાંથી મેળવેલ નીપજ કઈ છે:
- 52નીચે આપેલ પ્રક્રિયાને ધ્યાનમાં લો.View Solution
$MnO _{4}^{-}+8 H ^{+}+5 e ^{-} \rightarrow Mn ^{+2}+4 H _{2} O , E ^{\circ}=1.51 V$
$MnO _{4}^{-}$ નાં પાંચ મોલનું રિડક્ષન કરવા માટે વિદ્યુતનો જરૂરી જથ્થો ફેરાડે માં ........... છે. (પૂર્ણાક જવાબ)
- 53બેરિયમ ક્લોરાઇડ, સલ્ફ્યુરિક ઍસિડ અને હાઈડ્રોક્લોરિક ઍસિડ ની અનંત મંદન પર મોલર વાહકતાઓ અનુક્રમે $280,860$ અને $426 \,Scm ^{2}$ $mol ^{-1}$ છે બેરિયમ સલ્ફેટની અનંત મંદન પર મોલર વાહકતા $...... \,S cm ^{2} mol ^{-1}$ છેView Solution
- 54$298\, {~K}$ પર કોષ અચળાંક $1.14 \,{~cm}^{-1}$ સાથે વાહકતા કોષનો અવરોધ, જેમાં $0.001\, {M}\, {KCl}$ $1500 \,\Omega$ છે. $298\, {~K}$ પર $0.001\, {M}\, {KCl}$ દ્રાવણની મોલર વાહકતા $ 298 \, {~ K} $ $....$ ${S} \,{cm}^{2}\, {~mol}^{-1}$છે.(પૂર્ણાંક જવાબ)View Solution
- 55ગેલ્વેનિક કોષ માટે,View Solution
${Zn}({s})+{Cu}^{2+}(0.02 {M}) \rightarrow {Zn}^{2+}(0.04 {M})+{Cu}({s})$
${E}_{\text {cell }}=...... \,\times 10^{-2} \,{~V}$ { (નજીકના પૂર્ણાંકમાં) }
${\left[ {E}_{{Cu} / {Cu}^{2+}}^{0}=-0.34\, {~V}, {E}_{2 {n} / {Zn}^{2+}}^{0}=+0.76 \,{~V}\right.}$
$\left.\frac{2.303 {RT}}{{F}}=0.059\, {~V}\right]$
- 56યાદી $-I$ની યાદી $-II$ સાથે મેળ કરો:View Solution
યાદી $-I$
(પરિમાણ)
યાદી $-II$
(એકમ)
$(a)$ કોષ અચળાંક $(i)$ ${S}\, {cm}^{2} \,{~mol}^{-1}$ $(b)$ મોલર વાહકતા $(ii)$ પરિમાણરહિત $(c)$ વાહકતા $(iii)$ ${m}^{-1}$ $(d)$ વિદ્યુતવિભાજયનો વિયોજન અંશ $(iv)$ $\Omega^{-1} \,{~m}^{-1}$ નીચે આપેલા વિકલ્પોમાંથી સૌથી યોગ્ય જવાબ પસંદ કરો:
- 57વધારે પ્રમાણ વાળા ગરમ પાણીમાં જ્યારે $FeCl _{3}$ ઉમેરતાં પરિણામી કલિલમય કણોનાં ભાર (Charge) ની પ્રકૃતિ શું છે ?View Solution
- 58સંયોજન $A$ નો ઉપયોગ પ્રબળ ઓસિડેશનકર્તા તરીકે થાય છે અને તેની પ્રકૃતિ ઉભયગુણી છે. તે લેડ સંગ્રાહક બેટરીઓનો એક ભાગ છે. સંયોજન $A$ શોધો.View Solution
- 59$25^{\circ} {C}$ એ કોષને અનુસરો.View Solution
${Zn}\left|{Zn}^{2+}({aq}),(1 {M}) \| {Fe}^{3+}({aq}), {Fe}^{2+}({aq})\right| {Pt}({s})$
કોષ પોટેન્શિયલ $1.500\, {~V}$ પર ${Fe}^{3+}$ આયન તરીકે હાજર કુલ આયનનો અપૂર્ણાંક, ${X} \times 10^{-2}$ છે. $X$ નું મૂલ્ય $.....$ (નજીકના પૂર્ણાંકમાં) છે.
$\left(\right.$ આપેલ છે: $\left.E_{{Fe}^{3+} / {Fe}^{2+}}^{0}=0.77\, {~V}, {E}_{{Zn}^{2+} / {Zn}}^{0}=-0.76 \,{~V}\right)$
- 60${Cu}({s})\left|{Cu}^{2+}({aq})(0.1 {M}) \| {Ag}^{+}({aq})(0.01 {M})\right| {Ag}({s})$ કોષ માટે,કોષનો પોટેન્શિયલ ${E}_{1}=0.3095\, {~V}$View Solution
${Cu}({s})\left|{Cu}^{2+}({aq})(0.01 {M}) \| {Ag}^{+}({aq})(0.001 {M})\right| {Ag}({s})$ કોષ માટે ,કોષનો પોટેન્શિયલ $=.....\times 10^{-2} {~V}$
[ઉપયોગ : $\frac{2.303 {RT}}{{F}}=0.059$ ]
- 61જો $0^{\circ} {C}$ એ મરકયુરીની વાહકતા $1.07 \times 10^{6}$ ${S} \,{m}^{-1}$ હોય અને મરકયુરી ધરાવતા સેલનો અવરોધ $0.243\, \Omega$ છે,તો પછી કોષની કોષ અચળાંક ${x} \times 10^{4}\, {~m}^{-1}$ છે. ${x}$નું મૂલ્ય $......$ છે. (નજીકના પૂર્ણાંકમાં)View Solution
- 62જ્યારે એક કોષમાં કોષ અચળાંક $1.3 \,cm ^{-1}$ માપવામાં આવે છે ત્યારે $KCl$ નું $5.0\, m \,mol \,dm ^{-3}$ જલીય દ્રાવણ $0.55\, mS$ વાહકતા ધરાવે છે. તો આ દ્રાવણની મોલર વાહકતા ....... $mSm ^{2}\, mol ^{-1}$ છે. (નજીકનાં પૂર્ણાકમાં રાઉન્ડ ઓફ કરો)View Solution
- 63તાંબુ (કોપર) $NO _{3}^{-}$ નું $NO$ અને $NO _{2}$ માં રિડકશન કરે છે જે $HNO _{3}$ દ્રાવણની સાંદ્રતા પર આધારિત છે. (ધારી લો અપરિવર્તનીય (fixed) $\left[ Cu ^{2+}\right]$ અને $\left. P _{ NO }= P _{ NO _{2}}\right),$ ઉષ્માગતિકીય પ્રકૃતિ માટે, કોપર વડે $NO _{3}^{-}$ નું $NO$ અને $NO _{2}$ માં રિડક્શન $HNO _{3}$ ની કઈ સાંદ્રતા એ $10^{ x }\, M$ ને સમાન થશે. તો $2 x$ નું મૂલ્ય ...... છે.View Solution
(નજીકનાં પૂર્ણાંકમાં રાઉન્ડ ઑફ). $\left[\right.$ આપેલ $, E_{C u^{2+} / C u}^{o}=0.34\, V , E _{ NO _{3}^{-} / NO_2 }^{\circ}=0.96\, V$ $,E _{ NO _{3} / NO _{2}}^{\circ}=0.79 \,V$ $\left.\frac{ RT }{ F }(2.303)=0.059\right]$
- 64નિર્બળ એસિડની $HA$ની સાંદ્રતા $0.001\, {~mol}\, {~L}^{-1}$ અને વાહકતા $2.0 \times 10^{-5}\, {~S} \,{~cm}^{-1}$ છે.View Solution
જો $\Lambda_{{m}}^{\circ}$ $({HA})=190 \,{~S} \,{~cm}^{2} {~mol}^{-1}$, ${HA}$નો આયનીકરણ અચળાંક $\left({K}_{{a}}\right)$ $....\,\times 10^{-6}$ બરાબર છે.
- 65નીચેની પ્રક્રિયા સાથે કોષ ધારોView Solution
${Cu}_{({s})}+2 {Ag}^{+}\left(1 \times 10^{-3} \,{M}\right) \rightarrow {Cu}^{2+}(0.250\, {M})+2 {Ag}_{({s})}$
${E}_{{Cell}}^{\ominus}=2.97\, {~V}$
ઉપરની પ્રક્રિયા માટે ${E}_{\text {cell }}$ $=....\,V.$ (નજીકના પૂર્ણાંકમાં)
[આપેલ છે: $\log 2.5=0.3979, T=298\, {~K}]$
- 66નીચે બે નિવેદનો આપવામાં આવ્યા છેView Solution
વિધાન $I :$ ${CH}_{3} {COOH}$ (નિર્બળ વિદ્યુતવિભાજય)ની સરખામણીમાં ${KCl}$ (પ્રબળ વિદ્યુતવિભાજય) ની મર્યાદિત મોલર વાહકતા વધારે છે.
વિધાન $II :$ વિદ્યુતવિભાજયની સાંદ્રતામાં ઘટાડો સાથે મોલર વાહકતા ઘટે છે.
પ્રકાશમાં ઉપરોક્ત વિધાનોના , નીચે આપેલા વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો.
- 67પોટેશિયમ ક્લોરેટ નીચેના સમીકરણ દ્વારા બતાવ્યા પ્રમાણે ${KCl}$ના વિદ્યુત વિભાજય દ્વારા તૈયાર કરવામાં આવે છે.View Solution
$6 {OH}^{-}+{Cl}^{-} \rightarrow {ClO}_{3}^{-}+3 {H}_{2} {O}+6 {e}^{-}$
પોટેશિયમ ક્લોરેટ $10.0\, {~g}$ પેદા કરવા માટે $x\, A$નો પ્રવાહ $10\, h$ માટે પસાર કરવો પડે છે. ${x}$નું મૂલ્ય $.......$ છે. (નજીકના પૂર્ણાંકમાં)
(આણ્વિય દળ $\left.{KClO}_{3}=122.6 {~g} {~mol}^{-1}, {~F}=96500 {C}\right)$
- 68વાહકતાના $KCl$ દ્રાવણ $0.14\, S m ^{-1}$ વાહકતા કોષમાં $4.19 \,\Omega$ નો પ્રતિકાર બતાવે છે. જો સરખો કોષ $HCl$ થી ભરવામાં આવે .પ્રતિકાર $1.03 \,\Omega$.પર આવે છે. $HCl$ દ્રાવણ ની વાહકતા $....... \,\times 10^{-2} \,S m ^{-1}$.View Solution
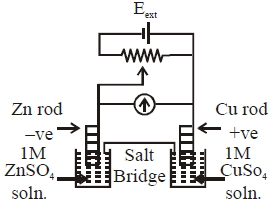
- 69$E _{ Cu ^{2+} \mid Cu }^{\circ}=+0.34 V$View Solution
$E _{ Zn ^{2}+\mid Zn }^{ o }=-0.76 V$
ઉપરોક્ત કોષ માટે નીચેના વિકલ્પોમાંથી ખોટા વિધાનની ઓળખ આપો
- 70$K$ માં $298\, K$ તાપમાને અપ્રમાણસર માટે $2 Cu ^{+}( aq ) \rightleftharpoons Cu ( s )+ Cu ^{2+}( aq )$ (જ્યાં $K$ એ સંતુલન અચળાંકછે ) ....... $\times 10^{-1}$View Solution
આપેલ $\left( E _{ Cu ^{2+} / Cu ^{+}}^{0}=0.16 V \right.$ $,E _{ Cu ^{+} / Cu }^{0}=0.52 V,$ $\left.\frac{ RT }{ F }=0.025\right)$
- 71આપેલ કોષ માટે: $Cu ( s )\left| Cu ^{2+}\left( C _{1} M \right) \| Cu ^{2+}\left( C _{2} M \right)\right| Cu ( s )$ .જો ગિબ્સ ઊર્જામાં ફેરફાર $(\Delta G )$ ઋણ છે તો,View Solution
- 72ગોલ્ડસ્મિથના વર્કશોપમાંથી મેળવેલ નકામું દ્રાવણ $250\ mL$ મળ્યું , જેમાં $0.1\, M AgNO _{3}$ અને $0.1\, M$ /$AuCl$ સમાવિષ્ટ છે. દ્રાવણને $1 \,A$ પ્રવાહ પસાર કરીને $2\, V$ પર $15 $ મિનિટ માટે ઇલેક્ટ્રોલાઇઝ્ડ કરવામાં આવ્યું હતું.કઈ ધાતુ/ધાતુઓ વિદ્યુતધનમય તરીકે હશે?View Solution
$\left(E_{A g^{+} / A g}^{0}=0.80\, V, E_{A n^{+} / A u}^{0}=1.69\, V\right)$
- 73જલીય દ્રાવણમાં વિદ્યુતવિભાજય $(X)$ ની સાંદ્રતા સાથે મોલરવાહકતાની વિવિધતા આપેલ આકૃતિમાં બતાવવામાં આવી છે.View Solution
વિદ્યુતવિભાજય $X$ શું છે?

- 74ડાઇક્રોમેટનો એસિડિક દ્રાવણ $ 2 $ $A$ કરંટ નો ઉપયોગ કરીને $ 8 $ મિનિટ માટે વિદ્યૂતવિભાજ્ય થાય છે. નીચેના સમીકરણ મુજબView Solution
$Cr _{2} O _{7}^{2-}+14 H ^{+}+6 e ^{-} \rightarrow 2 Cr ^{3+}+7 H _{2} O$
પ્રાપ્ત થયેલ $Cr ^{3+}$ નો જથ્થો $0.104$ ગ્રામ હતો.
આ પ્રક્રિયાની કાર્યક્ષમતા (\%માં) છે
(લઈએ : $F =96000\, C$, ક્રોમિયમ નું આણ્વિય દળ$=52$ )
- 75બેઝિક દ્રાવણમાં $KCl$ ના વિદ્યુતવિભાજન દ્વારા પોટેશિયમ ક્લોરેટ તૈયાર કરવામાં આવે છેView Solution
$6 OH ^{-}+ Cl ^{-} \rightarrow ClO _{3}^{-}+3 H _{2} O +6 e ^{-}$
જો પ્રવાહના માત્ર $60 \%$ નો ઉપયોગ પ્રક્રિયામાં કરવામાં આવે છે, તો $2\, A$ ના પ્રવાહની મદદથી $KCIO _{3}$ના $10\, g$નું ઉત્પાદન કરવા માટે જરૂરી સમય (નજીકના કલાકના પૂર્ણાંકમાં ફેરવો) છે ..........
(આપેલ છે: $F =96,500\, C\, mol ^{-1}$ $,$$ KClO _{3}$નું મોલર દળ $=122\,gmol ^{-1})$
- 76$298 \,K$ એ આપેલી પ્રકિયા માટે $\left[ Cu ^{2+}\right]=\left[ Sn^{2+}\right]=1\, M$ ગિબ્સ ઉર્જા શું હશે ?View Solution
$Cu ( s )+ Sn ^{2+}( aq ) \rightarrow Cu ^{2+}( aq )+ Sn ( s )$
$\left( E _{ Sn ^{2+} \mid Sn }^{0}=-0.16\, V , E _{ Cu ^{2+} \mid Cu }^{0}=0.34\, V \right.$ Take $F=96500\, C\, mol ^{-1}$ )
- 77$\mathrm{Cu}^{2+}{/ \mathrm{Cu}}$ અને $\mathrm{Cu}^{+}{/ \mathrm{Cu}}$ ના પ્રમાણિત પોટેન્શિયલ $\left(\mathrm{E}^{\circ}\right)$ અનુક્રમે $0.34 \;\mathrm{V}$ અને $0.522 \;\mathrm{V}$ છે. તો ${C u}^{2+}{/ {C u}^{+}}$ તો ${E}^{\circ}$ જણાવો.View Solution
- 78$ Na $માંથી ફોટોઇલેક્ટ્રિક પ્રવાહ (કાર્ય વિધેય , $\left. w _{0}=2.3\, eV \right)$ કોષના આઉટપુટ વોલ્ટેજ દ્વારા બંધ થઈ ગયું છેView Solution
$Pt ( s )\left| H _{2}( g , 1 bar )\right| HCl ( aq \cdot, pH =1)| AgCl ( s )| Ag ( s )$
જલીય $HCL $ માટે $K \left( w _{0}=2.25 eV \right),$ ફોટોઇલેક્ટ્રિક પ્રવાહને રોકવા માટે જરૂરી $pH$ ................$\times 10^{-2}$ છે, બાકીની બધી અન્ય શરતો તે જ રહે છે
અહી આપેલ $2.303 \frac{ RT }{ F }=0.06 V ; E _{ AgC1|Ag|C ^{-}}^{0}=0.22\, V$
- 79આપેલ અર્ધકોષ પ્રક્રિયા માટે $pH = 5$ પર વિધુતધ્રુવ પોટેન્શિયલ શું થશે ?View Solution
$2 \mathrm{H}_{2} \mathrm{O} \rightarrow \mathrm{O}_{2}+4 \mathrm{H}^{\oplus}+4 \mathrm{e}^{-} ; \mathrm{E}_{\mathrm{red}}^{0}=1.23 \mathrm{V}$ અને $ - 5 \times {10^{ - 4}}\,V\,{K^{ - 1}}$ છે. કોષપ્રક્રિયા $(\mathrm{R}=8.314 \;\mathrm{J} \mathrm{mol}^{-1} \mathrm{K}^{-1} ; \text { Temperature }=298 \;\mathrm{K} ;$ ઓક્સિજન એ પ્રમાણિત વાતાવરણ દબાણ $1$ બાર હેઠળ છે)
- 80તાપમાન સાથે સંતુલન અચળાંકના ફેરફાર નીચે આપેલ છેView Solution
તાપમાન $\quad$ સંતુલન અચળાંક
$\begin{array}{ll} T _{1}=25^{\circ} C & K _{1}=100 \\ T _{2}=100^{\circ} C & K _{2}=100\end{array}$
$T _{1}$ તાપમાને $\Delta H ^{\circ}, \Delta G ^{\circ}$ના મૂલ્યો અને $T _{2}$ તાપમાને $\Delta G ^{\circ}$નું મૂલ્ય ($kJ\, mol ^{-1}$ માં) અનુક્રમે , નજીક હશે?
$\left[\right.$ ઉપયોગ કરો : $\left. R =8.314\, JK ^{-1} mol ^{-1}\right]$
- 81View Solutionવિધાન જે અસત્ય છે તે જણાવો.
- 82$\mathrm{Sn}(\mathrm{s})\left|\mathrm{Sn}^{2+}(\mathrm{aq}, 1 \mathrm{M}) \| \mathrm{Pb}^{2+}(\mathrm{aq}, 1 \mathrm{M})\right| \mathrm{Pb}(\mathrm{s})$ વિધુતરાસાયણિક કોષ માટે જ્યારે કોષ સંતુલન પ્રાપ્ત કરે ત્યારે $\frac{\left[\mathrm{Sn}^{2+}\right]}{\left[\mathrm{Pb}^{2+}\right]}$ ગુણોત્તર જણાવો.View Solution
(આપેલ છે: $\mathrm{E}_{\mathrm{Sn}^{2+} / \mathrm{Sn}}^{0}=-0.14 \mathrm{\;V}$ $\left.\mathrm{E}_{\mathrm{Pb}^{+2}/{\mathrm{Pb}}}^{0}=-0.13 \;\mathrm{V}, \frac{2.303 \mathrm{RT}}{\mathrm{F}}=0.06\right)$
- 83$0.1$ ફેરાડે વિધુતનો ઉપયોગ કરી પ્લેટિનમના ધુવો વચ્ચે $Ni(NO_3)_2$ ના દ્રાવણ વિધુતવિભાજન કરવામાં આવે છે. કેથોડ પર કેટલા મોલ $Ni$ જમા થશે ?View Solution
- 84$300\, K$ એ એક કોષનો પ્રમાણિત ઇલેક્ટ્રોડ પોટેન્શિયલ (વિભવ) $2\, V$ છે. $300\, K$ એ આપેલ પ્રક્રિયા માટે અંદાજીત સંતુલન અચળાંક $(K)$ કેટલો હશે?View Solution
$Zn\,(s)\,\, + \,\,C{u^{2 + }}\,(aq)\, \rightleftharpoons \,Z{n^{2 + \,}}\,(aq)\, + Cu\,(s)$
$(R = 8 \,JK^{-1}\,mol^{-1},\, F = 96000\,C\,mol^{-1})$
- 85$C{o^{3 + }}{e^ - } \longrightarrow C{o^{2 + }};\,{E^o} = 1.81\,V$View Solution
$P{b^4} + 2{e^ - } \longrightarrow P{b^{2 + }};\,{E^o} = + 1.67\,V$
$C{e^{4 + }} + {e^ - } \longrightarrow C{e^{3 + }};\,{E^o} = + 1.61\,V$
$B{i^{3 + }} + 3{e^ - } \longrightarrow Bi;\,{E^o} = + 0.20\,V$ આપેલ છે. તો આ ઘટકતી ઓક્સિડેશતકર્તા તરીકેની ક્ષમતા ક્યા ક્રમમાં વધશે?
- 86$E_{{O_2}/{H_2}O}^o = + 1.23\,V$; $E_{{S_2}O_8^{2 - }/SO_4^{2 - }}^o = 2.05\,V$; $E_{B{r_2}/B{r^ - }}^o = +1.09\,V$; $E_{A{u^{3 + }}/Au}^o = 1.4\,V$ આપેલ છે. તો સૌથી પ્રબળ ઓક્સિડેશનકર્તા જણાવો.View Solution
- 87$NaCl,\,HCl$ અને $NaA$ ના માટે $ \wedge _m^o$ અનુક્રમે $126.4, 425.9$ અને $100.5\,\,S\,cm^2\,mol^{-1},$ છે. જો $0.001\,M\,HA$ ની વાહકતા $5\times 10^{-5}\,S\,cm^{-1},$ હોય તો $HA$ નો વિયોજન અંશ કેટલો થાય?View Solution
- 88આપેલ પ્રક્રિયાView Solution
$Cu(s) + 2Ag{^+}_{(aq)} \to Cu^{+2}_{(aq)} + 2Ag(s)$
માટે સંતુલન અચળાંક $K_C = 10 \times 10^{15}$ છે, તો $298\, K$ ને $E_{cell}^o$ નું મૂલ્ય કેટલુ થશે?
[${2.303\,\frac{{RT}}{F}}$ એ $298\,K$ $=0.059\,V$]
- 89આપેલા કોષ $Zn(s)|\,Z{n^{2 + }}(aq)\,||\,{M^x}\, + \,(aq)|\,M(s),$ માટે જુદા-જુદા અર્ધકોષો અને તેમના પ્રમાણિત ધ્રુવ પોટેન્શિય નીચે મુજબ છે.View Solution
$M^{x+}\, (aq)\,/M(s)$ $A{u^{3 + }}(aq)/$
$Au(s)$
$A{g^ + }(aq)/$
$Ag(s)$
$F{e^{3 + }}(aq)/$
$F{e^{2 + }}(aq)$
$F{e^{2 + }}(aq)/$
$Fe(s)$
$E^o\,M^{x+}$ $\,/M(V)$ $1.40$ $0.80$ $0.77$ $-0.44$
જો $E_{Z{n^{2 + }}/Zn}^o = - 0.76\,V,$ હોય તો, ક્યો કેથોડ પ્રતિ ઇલેક્ટ્રોન ફેરફાર માટે $E_{cell}^o$ નું મહત્તમ મૂલ્ય આપશે
- 90આપેલા કોષ માટે $298\,K$ પર પ્રમાણિત ગિબ્સ મુક્ત ઊર્જા $kJ\,mol^{-1}$ માં ગણો.View Solution
$Zn(s)\, + \,C{u^{2 + }}(aq)\, \to \,Z{n^{2 + }}(aq) + Cu\,(s)$
$(298\,K$ પર ${E^o} = 2\,V,$ ફેરાડે અચળાંક $F = 96500\, C\, mol^{-1})$
- 91જ્યારે $10^{- 6}$ મોલલ $HCI$ ના દ્રાવણનો ઉપયોગ કરવામાં આવે ત્યારે એક કોષ,View Solution
$Pt(s)| H_2 (g,1\,bar)| HCl(aq)| AgCl(s)| Ag(s)| Pt(s)$
માટે કોષ પોટેન્શિયલ $0.92\, V$ છે. તો $(AgCl / Ag,Cl^- )$ ઇલેક્ટ્રોડનો પ્રમાણિત ઇલેક્ટ્રોડ પોટેન્શિયલ કેટલા ........... $\mathrm{V}$ હશે?
{ આપેલ $\frac{2.303RT}{F} = 0.06\,V \,\,298\,K $એ }
- 92નીચેની રીડક્શન પ્રક્રિયાઓને ધ્યાનમાં લોView Solution
$Zn^{2+} + 2e^-$ $\longrightarrow$ $Zn (s) ; E^o = -0.76\,V$
$Ca^{2+} + 2e^-$ $\longrightarrow$ $Ca (s) ; E^o = -2.87\,V$
$Mg^{2+} + 2e^-$ $\longrightarrow$ $Mg (s) ; E^o = -2.36\,V$
$Ni^{2+} + 2e^-$ $\longrightarrow$ $Ni (s) ; E^o = -0.25\,V$
ધાતુઓની રિડક્શનકર્તા ઉર્જાનો ચઢતો ક્રમ કયો થશે?
- 93મોલર વાહકતા $({\Lambda _m})$ વિરુદ્ધ $\sqrt C$ ના નીચે આપેલા આલેખ પૈકી ક્યો એક સાચો છે ?View Solution
- 94લેડ એસિડ બેટરીના એનોડિક અર્ધકોષ ને $0.05$ ફેરાડે વિજપ્રવાહનું ઉપયોગ કરી રિચાર્જ કરવામાં આવે છે. તો આ પ્રક્રિયામાં દરમ્યાન $PbSO_4$ ના કેટલા ગ્રામ વિદ્યુત વિભાજીત થશે? $(PbSO_4$ નું મોલર દળ $= 303\, g \,mol^{-1})$View Solution
- 95વિધાનો $S_1$ અને $S_2$ ધ્યાનમાં લો.View Solution
$S_1$: વિધુતવિભાજયની સાંદ્રતા ઘટતા વાહકતા હંમેશા વધે છે.
$S_2$: વિધુતવિભાજચતી સાંદ્રતા ઘટતા મોલર વાહકતા હંમેશા વધે છે.
- 96જે કોષમાં નીચેની પ્રક્રિયા થતી હોય તેવા કોષનો પ્રમાણિત કોષ પોટેન્શિયલ ($V$ માં) ગણો.View Solution
$F{e^2}+ \left( {aq} \right) + A{g^ + }\left( {aq} \right) \to F{e^{3 + }}\left( {aq} \right) + Ag\left( s \right)$
$E_{Ag^+/Ag}^o = xV$, $E_{F{e^{2 + }}/Fe}^o = yV$, $E_{F{e^{3 + }}/Fe}^o = zV$
- 97જ્યારે એસિડિક પાણીમાંથી વિધુતપ્રવાહ પસાર કરવામાં આવે ત્યારે $965\,seconds$ માં $NTP$ એ $112\,mL$ હાઇડ્રોજન વાયુ એકઠો થાય છે. તો પસાર કરેલો પ્રવાહ એમ્પિયરમાં જણાવો.View Solution
- 98જ્યારે એસિડિક માધ્યમમાં, નાઇટ્રોબેન્ઝિનમાંથી $9.65$ એમ્પિયરનો પ્રવાહ $1.0$ કલાક માટે પસાર કરવામાં આવે ઉત્પન્ન થતા $p$ - એમિનો ફિનોલનો જથ્થો .............. $\mathrm{g}$ જણાવો.View Solution
- 99આપેલ $E^o_{Cl_2/Cl^-} = 1.36\,V,$ $E^o_{Cr^{3+}/Cr}= -0.74\,V,$View Solution
$E^o_{Cr_2/O_7^{2-}/Cr^{3+}}=1.33\,V,$ $E^o_{MnO^-_4/Mn^{2+}} = 1.51\,V$
તો નીચેના પૈકી સૌથી પ્રબળ રિડક્શતકર્તા ..........
- 100$Fe^{3+} \to Fe$ માટે પ્રમાણિત રિડકશન પોટેન્શિયલ $(E^o)$ ............... $\mathrm{V}$View Solution
આપેલ :
$F{e^{2 + }} + 2{e^ - } \to Fe;$ ${E^o}_{F{e^{2 + }}/Fe} = - 0.47\,V$
$F{e^{3 + }} + {e^ - } \to F{e^{2 + }};$ ${E^o}_{F{e^{3 + }}/F{e^{2 + }}} = + 0.77\,V$