Question Bank
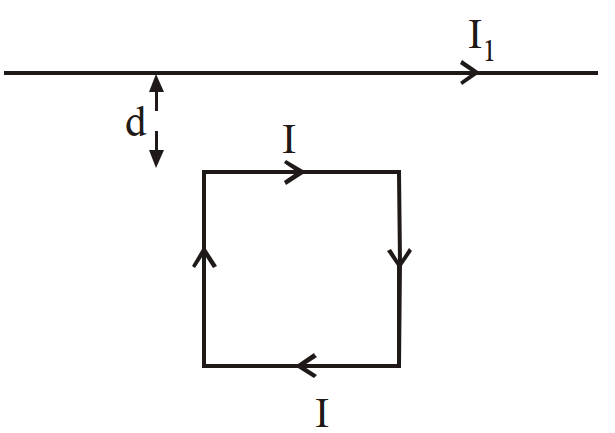
Explore our large set of questions to practice for your standard seamlessly- 1चित्रानुसार एक लम्बे सीधे तार से एक अपरिवर्ती (स्थिर) धारा $I _1$ प्रवाहित हो रही है। इस तार से $d$ दूरी पर, क्षैतिज तल में, एक वर्गाकार लूप (पाश) रखा है, जिससे एक स्थिर (अपरिवर्ती) धारा I प्रवाहित हो रही है। तो, लूप (पाश) पर :View Solution
- 2किसी $G$ प्रतिरोध के धारामापी पर $S$ ओम प्रतिरोध का शंट लगाया गया है। मुख्य धारा का मान अपरिवर्तित रखने के लिए धारामापी के श्रेणीक्रम में लागये गये प्रतिरोध का मान होगा:View Solution
- 3किसी $R$ त्रिज्या के पतले छल्ले (रिंग) पर $q$ आवेश समानरूप से विस्तारित (फैला) है। यह छल्ला अपनी अक्ष के परितः एकसमान आवृत्ति $fHz$ से घूर्णन करता है। तो इसके केन्द्र पर चुम्बकीय-प्ररेण का मान होगा:View Solution
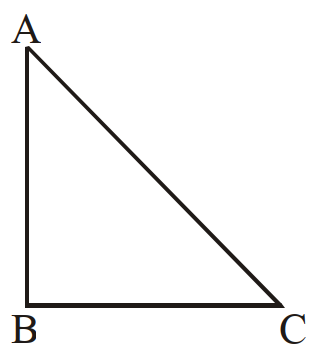
- 4समकोण समद्विबाहु त्रिभुज के आकार के एक बन्द पाश $ABC$ में विद्युत धारा प्रवाहित हो रही है। इसे किसी एकसमान $AB$ दिशा के अनुदिश चुम्बकीय क्षेत्र में रखा गया है। यदि भुजा $BC$ पर चुम्बकीय बल $\overrightarrow{ F }$ हो तब भुजा $AC$ पर बल होगा:View Solution
- 5View Solutionकिसी क्षेत्र में, एकसमान विद्युत और एकसमान चुम्बकीय क्षेत्र एक ही दिशा के अनुदिश कार्य कर रहे हैं। यदि इस क्षेत्र में एक इलेक्ट्रॉन इस प्रकार प्रक्षेपित किया जाये कि उसके वेग की दिशा, क्षेत्रों की दिशा में हो तो इलेक्ट्रॉन:
- 6किसी गेल्वेनोमीटर की कुंडली का प्रतिरोध $100 \Omega$ है और $30 mA$ की विद्युतधारा से इसके पूरे पैमाने (स्केल) पर विक्षेप होता है। यदि इसे 30 वोल्ट परास के वोल्टमीटर में परिवर्तित करना है तो कितना प्रतिरोध और लगाना ( जोड़ना) होगा?View Solution
- 7एक वर्गाकार पाश (लूप) को, जिससे विद्युतधारा प्रवाहित हो रही है, किसी एकसमान चुम्बकीय क्षेत्र में लटकाया गया है। चुम्बकीय क्षेत्र पाश (लूप) के समतल में कार्य करता है। यदि पाश की किसी एक भुजा पर $\vec{F}$ बल लगता है तो, शेष तीन भुजाओं पर नेट बल हैView Solution
- 8किसी $R$ मीटर त्रिज्या के किसी छल्ले (वलय) पर $q$ कूलॉम आवेश एक समान रूप से फैला हुआ है। यह छल्ला अपनी अक्ष पर $f$ परिक्रमण प्रति सैकंड की आवृति से घूर्णन करता है। छल्ले के केन्द्र पर चुम्बकीय प्रेरण का मान $Wb / m ^2$ में हैView Solution
- 9अचर चुम्बकीय फील्ड के प्रभाव में एक आवेशित कण त्रिज्या $R$ के वृत्त में अचर चाल $v$ से चलता है। इसके घूमने का समय अन्तराल :-View Solution
- 10एक गेल्वेनोमीटर के कॉयल का प्रतिरोध $60 \Omega$ है और $1.0$ ऐम्पीयर धारा के लिए पूर्ण स्केल का विचलन दिया है। इसे $5.0$ ऐम्पीयर तक पढ़ने वाले ऐमीटर में बदलने के लिए:-View Solution
- 11एक आवेशित कण पर आवेश का मान $-2 \mu C$ है। यह $y$ दिशा में क्रियाकारी $2 T$ के चुम्बकीय क्षेत्र में वेग $(2 \hat{ i }+3 \hat{ j }) \times 10^6 ms ^{-1}$ से चल रहा हो तो इस पर क्रियाकारी चुम्बकीय बल होगा:-View Solution
- 12$0.2$ मीटर त्रिज्या की एक वृत्ताकार डिस्क को $\frac{1}{\pi}\left(\right.$ वेबर/मी $\left.{ }^2\right)$ प्रेरण के अचर चुम्बकीय क्षेत्र में इस प्रकार रखा है कि इसका अक्ष चुम्बकीय-क्षेत्र के साथ $60^{\circ}$ का कोण बनाता है। डिस्क से सम्बन्धित चुम्बकीय फ्लक्स होगा :View Solution
- 13View Solution
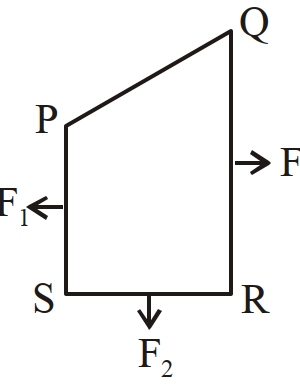
एक धारा वाहक बन्द लूप(तार फन्द) PQRS को अचल चुम्बकीय फील्ड में रखा गया है। यदि लूप भागों PS, SR, और $RQ$ पर क्रमानुसार चुम्बकीय बल $F_1, F_2$ और $F_3$ क्रियाकारी हों और यह कागज़ पृष्ठ के तल में संकेतित दिशाओं में हों तो भाग $QP$ पर क्रियाकारी बल होगा : - 14द्रव्यमान $m$, आवेश $Q$ और गतिज ऊर्जा $T$ का एक कण उत्प्रेरण $\overrightarrow{ B }$ के अनुप्रस्थ अचर चुम्बकीय फील्ड ( क्षेत्र) में प्रवेश करता है। तीन सैकण्ड के उपरान्त इस कण की गतिज ऊर्जा होगी :View Solution
- 15View Solutionइलेक्ट्रॉनों का एक किरण समूह परस्पर लम्बवत् विद्युत और चुम्बकीय क्षेत्रों में से अविक्षिप्त चला जाता है। यदि विद्युत क्षेत्र को बन्द कर दिया जाये और चुम्बकीय क्षेत्र को अपरिवर्तित रखा जाये तो इलेक्ट्रॉनों का चलन होगा-
- 16आयनों के द्रव्यमान मापने के लिये एक द्रव्यमान मापी स्पैक्ट्रोमीटर में आयनों को पहले वैद्युत विभव $V$ द्वारा त्वरित कर फिर चुम्बकीय क्षेत्र $B$ का प्रयोग कर $R$ त्रिज्या के अर्धवृत्तीय पथ पर चलाया जाता है। यदि $V$ और $B$ को स्थिरमानी रखा जाये तो अनुपात अनुपाती होगा-View Solution
- 17आवेश $q$ का एक कण त्रिज्या $R$ के वृत्ताकार मार्ग में चाल $v$ के साथ चल रहा है। इससे सम्बन्धित चुम्बकीय आघूर्ण $\mu$ का मान होगा-View Solution
- 18एक अचर चुम्बकीय क्षेत्र के प्रभाव में एक आवेशित $\text{d . kff ; kR}$ के वृत्त में स्थिर चाल $v$ से चल रहा है। इस चलन के समय अन्तरालView Solution
- 19View Solutionदो कुण्डली 1 व 2 समान तार से बनी है। पहली की त्रिज्या दूसरी से दोगुनी है। कितना विभव दोनों पर लगाया जाए कि दोनों के केन्द्रों पर चुम्बकीय क्षेत्र तीव्रता समान हो?
- 20एक आवेशित कण $\overrightarrow{ v }$ वेग से चुम्बकीय क्षेत्र $\overrightarrow{ B }$ में चलता है। इस पर कार्यरत बल शून्य नहीं है तो यह दर्शाता है किView Solution
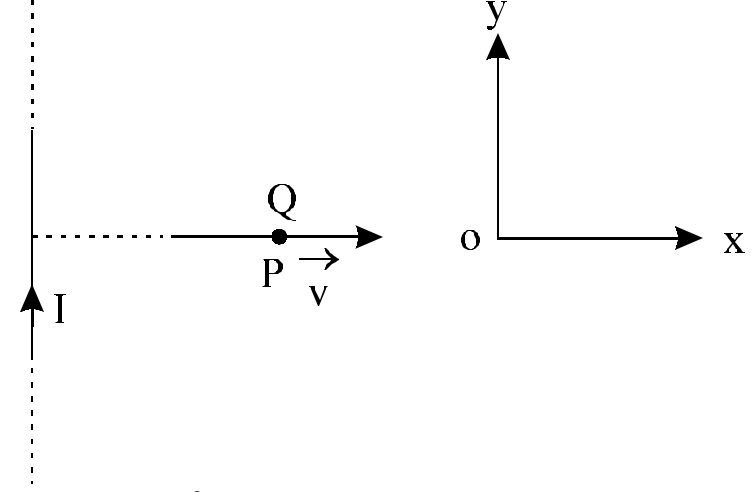
- 21एक लम्बे तार में I धारा प्रवाहित होती है। किसी क्षण एक $Q$ आवेश $P$ बिन्दु पर $v$ वेग से चलता है तो बल होगाView Solution
- 22एक गेल्वेनोमीटर $50 \Omega$ प्रतिरोध तथा $25$ विभाजनों का है। $4 \times 10^{-4} A$ धारा इसमें एक प्रति विभाजन विक्षेप पेदा करता है। इसे $25 V$ का वोल्टमीटर बनाना है तो निम्न में से कौन सा प्रतिरोध जोड़ना होगा?View Solution
- 23एक इलैक्ट्रान एक समान वेग $v$ से वृतीय पथ पर गति करता है। इससे केन्द्र पर एक चुम्बकीय क्षेत्र $B$ बनता है। तो वृत की त्रिज्या निम्न में से किसके समानुपाती होगी?View Solution
- 24View Solutionएक आवेशित कण चुम्बकीय क्षेत्र के लम्बवत् गति करता है तो-
- 25एक धारावाही परिनालिका अपने अक्ष के अनुदिश चुम्बकीय क्षेत्र $B$ उत्पन्न करती है। यदि धारा दोगुनी तथा फेरों की संख्या प्रति सेमी आधी कर दी जाए तो नया चुम्बकीय क्षेत्र होगा$-$View Solution
- 26एक नियत लम्बाई के तार से बनाई गयी एक फेरे की कुण्डली में धारा प्रवाहित करने पर इसके केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र $B$ है। यदि उसी तार से दो फेरों की कुंडली बनायी जाये तथा उतनी ही धारा प्रवाहित की जाये, तो कुण्डली के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र होगा:View Solution
- 27View Solutionएक गेल्वैनोमीटर को वोल्टमीटर में बदल सकते हैं जब
- 28एक आवेश $q , v$ वेग से चुम्बकीय क्षेत्र $\overline{ B }$ तथा वैद्युत क्षेत्र $\overrightarrow{ E }$ में गति करता है। इस पर लगने वाला बल होगा-View Solution
- 29एक स्थान पर वैद्युत क्षेत्र $\overrightarrow{ E }$ तथा चुम्बकीय क्षेत्र $\overrightarrow{ B }$ एक दूसरे के लम्बवत् लगे हैं। एक इलैक्ट्रॉन इन दोनों क्षेत्रों के लम्बवत् गति करता है तो वह अविक्षेपित रहता है। इलैक्ट्रान का वेग है :View Solution
- 30एक आवेशित वस्तु जिसका आवेश $q$ तथा द्रव्यमान $m$ है चुम्बकीय क्षेत्र $B$ के लम्बवत् गति करता है। वस्तु की ऊर्जा $E$ है तो इसकी घूर्णन आवृत्ति होगीView Solution
- 31दो समांतर तार $P \& Q$ एक दूसरे के लम्बवत् समतल में $5$ मीटर की दूरी पर रखे हैं। इनमें धारा का मान क्रमश: $2.5 A$ तथा $5 A$ है जो समान दिशाओं में चलती है। उनके मध्यवर्ती बिन्दु पर चुम्बकीय क्षेत्र हैView Solution
- 32एक प्रोटॉन $3 \times 10^5$ मी/सेकंड के वेग से $0.3 T$ वाले चुम्बकीय क्षेत्र में $30^{\circ}$ का कोण बनाते हुए गति करता है। इसकी पथ की त्रिज्या होगी (प्रोटॉन का $e / m =10^8$ कूलाम/किग्रा)View Solution
- 33View Solutionएक खोखले बेलन में धारा प्रवाहित होती है तो इसमें उत्पन्न चुम्बकीय क्षेत्र होगा
- 34एक प्रोटॉन $1 V$ पर त्वरित किया गया है। इसकी गतिज ऊर्जा होगीView Solution
- 35View Solutionएक लम्बे तार से एक, एक फेरे वाली कुण्डली तथा फिर उसी तार से 2 फेरों वाली कुण्डली बनायी जाती है। यदि दोनों में प्रवाहित धारा एक समान है तो उनके केन्द्र पर चुम्बकीय क्षेत्र तीव्रताओं का अनुपात होगा-
- 36एक गैल्वेनोमीटर का प्रतिरोध $8 \Omega$ है। इसमें $2 \Omega$ का शण्ट प्रतिरोध लगाया गया। इसमें $1 A$ धारा प्रवाहित होती है तो बताओ शण्ट में कितनी धारा प्रवाहित होगी?View Solution
- 37दो समान्तर तार एक दूसरे से 1 मीटर दूरी पर रखे हैं, इनमें $1 A$ धारा प्रवाहित होती है। प्रति एकांक लम्बाई पर आकर्षण बल होगा-View Solution
- 38एक कुण्डली जिसकी त्रिज्या $0.5$ मीटर, फेरों की संख्या $50$ तथा धारा का मान $2 A$ है तो उसके केन्द्र पर चुम्बकीय क्षेत्र तीव्रता होगी $:-$View Solution
- 39View Solutionएक धनात्मक आवेश एक समान चुम्बकीय क्षेत्र (ऊर्ध्वाधरतः दिष्ट) में पूर्व की ओर गति करता है, आवेश:
- 40दो धारावाही चालक एक दूसरे के लम्बवत् रखे हैं। $AB$ तथा $CB$ एक दूसरे के लम्बवत् हैं तो तुल्य चुम्बकीय क्षेत्र तीव्रता कहां शून्य होगीView Solution
- 41एक $10 eV$ ऊर्जा का एक इलैक्ट्रॉन चुम्बकीय क्षेत्र $10^{-9}$ वेबर/मी. $(1 G )$ के लम्बवत् गति करता है तथा दोनों ध राओं से symmetrical हैं। तो इसके पथ की त्रिज्या होगीView Solution
- 42एक गेल्वैनोमीटर जिसका प्रतिरोध $20 \Omega$ है, $0.004 A$ धारा पर पूरा स्केल विक्षेप देता है। इसे एक $1 A$ रेंज वाले एमीटर बनाने के लिए कितना शण्ट प्रतिरोध देना होगा?View Solution
- 43एक छोटे धारावाही तार (dl) की वजह से $r$ दूरी पर बना चुम्बकीय क्षेत्र $( dB )$ होगाView Solution
- 44एक स्थान पर चुम्बकीय क्षेत्र $B =0.5 T$ तथा वैद्युत क्षेत्र $E =20$ वोल्ट/मी एक दूसरे के लम्बवत् लगते हैं। एक इलैक्ट्रॉन पुंज समान गति से इन क्षेत्रों में दोनों के लम्बवत् चलता है तो इलैक्ट्रॉन की वेग होगीView Solution
- 45एक तार जिसमें $12 A$ धारा प्रवाहित होती है उससे किसी दूरी पर चुम्बकीय क्षेत्र तीव्रता $3 \times 10^{-6}$ वेबर $/$ मी $^2$ है। इस दूरी का मान होगाView Solution
- 46एक तार का व्यास $0.5$ मिमी है। इसमें $1 A$ धारा प्रवाहित होती है। इसके एक दूसरे तार जिसका व्यास 1 मिमी है तथा इसमें भी $1 A$ धारा प्रवाहित होती है से बदल दिया जाता है। तो तार से कुछ दूरी पर चुम्बकीय क्षेत्र तीव्रता होगी-View Solution
- 47View Solutionएक स्थान पर एक समान चुम्बकीय क्षेत्र (B) तथा वैद्युत क्षेत्र (E) एक दूसरे के लम्बवत् लगाये गये हैं। इसमे एक इलैक्ट्रॉन चलता है, तो-
- 48View Solutionएक धारा प्रवाहित कुण्डली यदि एक समान चुम्बकीय क्षेत्र में रखी गयी है तो उसमें
- 49एक चुम्बकीय क्षेत्र $X$-अक्ष की ऋणात्मक दिशा में है इसमें एक आवेश $v$ वेग से $X$-अक्ष की धनात्मक दिशा में गति करता है तो आवेश रहेगाView Solution
- 50एक सीधे तार में धारा $i$ प्रवाहित होती है तो उसमें दूरी $r$ पर चुम्बकीय क्षेत्र तीव्रता $0.4 T$ है। $2 r$ दूरी पर चुम्बकीय क्षेत्र तीव्रता होगी-View Solution
- 51View Solutionएक गैल्वेनोमीटर को एक एमीटर में बदलने हेतु हमे जोड़ना चाहिए
- 52एक सीधे तार में $1.2 A$ की धारा प्रवाहित होती है। इससे $0.5$ मीटर दूरी पर चुम्बकीय क्षेत्र तीव्रता $2 T$ है। चुम्बकीय क्षेत्र तार की लम्बाई के लम्बवत् है तो तार पर लगने वाला बल हैView Solution
- 53एक ड्यूट्रॉन एक दिये हुए चुम्बकीय क्षेत्र $B$ के लम्बवत् तल में $0.5$ मीटर वाले वृत्तीय पथ पर गति करता है। इसकी गतिज ऊर्जा $50 \ keV$ है। यदि इस वृतीय पथ पर तथा इसी चुम्बकीय क्षैत्र में प्रोट्रॉन गतिमय हो तो इसकी गतिज ऊर्जा होगी-View Solution
- 54View Solutionएक समान चुम्बकीय क्षेत्र इलैक्ट्रान की गति के लम्बवत् दिशा में लगाया जाता है। इसके कारण यह एक इलैक्ट्रान 2 सेमी वाले वृतीय पथ पर घूमता है। यदि इलैक्ट्रान का वेग दोगुना कर दिया जाए तो पथ की त्रिज्या होगी:
- 55View Solutionएक चालक लूप को यदि चुम्बकीय क्षेत्र में चलाया जाए तो उसमें उत्पन्न होने वाला आवेश का कारण है
- 56एक लम्बे धारा प्रवाहित तार की वजह से किसी बिन्दु $P$ पर जो तार से $4$ सेमी दूर है, चुम्बकीय क्षेत्र तीव्रता $10^{-3} T$ है। तो $12$ सेमी दूर स्थित बिन्दु पर चुम्बकीय क्षेत्र तीव्रता ज्ञात करो।View Solution
- 57View Solutionएक धारा प्रवाहित कुण्डली में ऊर्जा किस रूप में संचित होती है?
- 58View Solutionटेस्ला मात्रक है-
- 59View Solutionएक धारा प्रवाहित कुण्डली एक समान चुम्बकीय क्षेत्र में रखी गयी है। कुण्डली कितने कोण से घूमे कि उसका समतल
- 60View Solutionचुम्ककीय सुग्राहिता ऋणात्मक होती है :
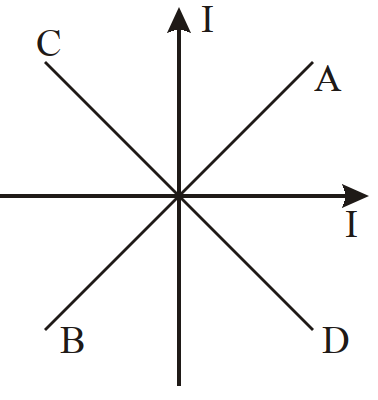
- 61आरेख में दंड (छड़) चुम्बकों की व्यवस्थाओं के विन्यास दिये गये हैं। प्रत्येक चुम्बक का द्विध्रुव आघूर्ण $m$ है। किस विन्यास में नेट चुम्बकीय द्विध्रुव आघूर्ण का मान अधिकतम होगा ?View Solution
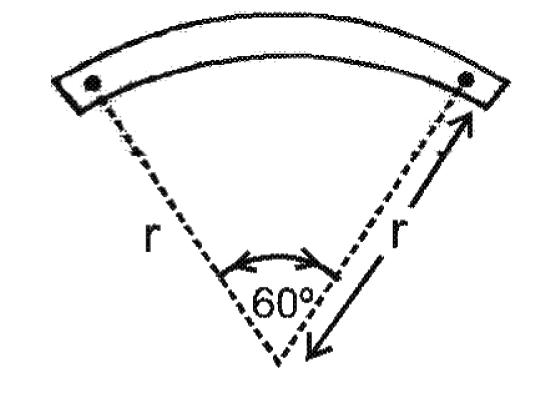
- 62एक छड़ (दंड) चुम्बक की लम्बाई ' 1 ' है और इसका चुम्बकीय द्विध्रुव बल-आघूर्ण ' $M$ ' है। यदि इसे आरेख (चित्र) में दिये गये अनुसार एक चाप के आकार में मोड़ दिया जाय तो, इसका नया चुम्बकीय द्विध्रुव बलआघूर्ण होगा:View Solution
- 63किसी चुम्बकीय क्षेत्र में समान्तर लटकी चुम्बकीय सुई को $60^{\circ}$ घुमाने के लिये $\sqrt{3} J$ कार्य की आवश्यकता होती है तो, इस सुई को उसी स्थिति में बनाये रखने के लिये आवश्यक बल$-$आघूर्ण $($टॉर्क$)$ का मान होगा:View Solution
- 64View Solutionएक चुम्बकीय सुई क्षैतिज समतल में घूम सकती है। यदि इसे किसी भूचुम्बकीय ध्रुव पर ले जायें तो यह :
- 65चुम्बकीय आघूर्ण $0.4 J T ^{-1}$ के एक छोटे (दंड) चुम्बक को किसी ऐसे एकसमान चुम्बकीय क्षेत्र में रखा गया है जिसकी तीव्रता $0.16 T$ है। यह चुम्बक स्थिर संतुलन में होगा। यदि इसकी स्थितिज ऊर्जा हो:View Solution
- 66चार हल्की छड़ों $A , B , C , D$ को धागों से अलग-अलग लटकाया गया है। एक छड़ (दंड) चुम्बक को धीरे-धीरे प्रत्येक के पास लाया जाता है और निम्नलिखित प्रेक्षण नोट किये जाते हैं: (i) $A$ हल्की सी प्रतिकर्षित होती है (ii) $B$ हल्की सी आकर्षित होती है (iii) $C$ बहुत अधिक आकर्षित होती है (iv) $D$ अप्रभावित रहती है तो निम्नलिखित में से कौन-सा कथन ठीक है?View Solution
- 67View Solutionकिसी प्रतिचुम्बकीय परमाणु का चुम्बकीय आघूर्ण होता है
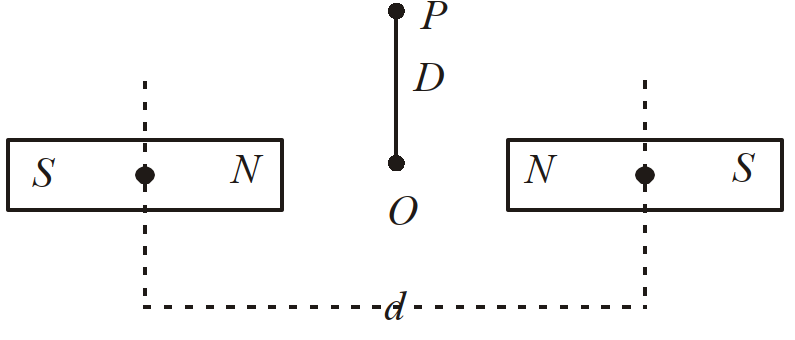
- 68दो सर्वसम (समरूप) छड़ चुम्बकों को इस प्रकार स्थिर किया गया है कि उनके केन्द्र $d$ दूरी पर हैं। चित्र में दिखाये गये अनुसार दोनों चुम्बकों के बीच के खाली स्थान के मध्य बिन्दु $O$ से, $D$ दूरी पर, बिन्दु $P$ पर एक आवेश $Q$ रखा है। $Q$ आवेश पर बल हैView Solution
- 69View Solutionविद्युत चुम्बक नर्म लोहे से बनाये जाते हैं। क्योंकि लोहे में होती है
- 70चुम्बकीय याम्योत्तर में स्थिति किसी कम्पन चुम्बकत्वमापी पर एक छोटा चुम्बक रखा है। यह चुम्बक पृथ्वी के क्षैतिज चुम्बकीय क्षेत्र में जिसका मान $24$ माइक्रोटेस्ला है, $2$ सेकण्ड के आवृति काल से दोलन करता है। जब एक विद्युत वाहित तार रखकर पृथ्वी के क्षेत्र की विपरीत दिशा में, $18$ माईक्रोटेस्ला का एक क्षैतिज उत्पन्न किया जाता है, तो चुम्बक का नया आर्वतकाल होगाView Solution
- 71View Solutionएक प्रतिचुम्बकीय पदार्थ को एक छड़ चुम्बक के उत्तरी ध्रुव अथवा दक्षिणी ध्रुव के निकट लाया जाये तो यह:-
- 72$2 \times 10^4 JT ^{-1}$ चुम्बकीय आघूर्ण का एक छड़ चुम्बक एक क्षैतिज तल में स्वतन्त्र रूप से घूम सकता है। इस स्थान पर $B =6 \times 10^{-4} T$ का क्षैतिज चुम्बकीय क्षेत्र क्रियाकारी है। क्षेत्र दिशा के समान्तर दिशा से चुम्बक को धीरे$-$धीरे क्षेत्र दिशा से $60^{\circ}$ की दिशा तक ले जाने में किया गया कार्य होगा$:-$View Solution
- 73View Solutionक्यूरी ताप ऐसा ताप होता है जिससे ऊपर :
- 74View Solutionकमरे के तापक्रम पर 'निकिल' लौह-चुम्बकत्व गुण दर्शाता है। यदि तापक्रम को क्यूरी तापक्रम से अधिक कर दें तो निकिल प्रदर्शित करेगा-
- 75एक प्रतिचुम्बकीय, अनुचुम्बकीय तथा लौहचुम्बकीय पदार्थों का चुम्बकीय द्विध्रुव आघूर्ण $\mu_{ d }, \mu_{ p }, \mu_{ f }$ है तोView Solution
- 76क्यूरी नियम के अनुसार चुम्बकीय शीलता, पदार्थ के तापमान $T ( K )$ के समानुपाती हैView Solution
- 77View Solutionप्रति चुम्बकीय पदार्थों में उत्पन्न चुम्बकीय क्षेत्र चलेगा
- 78एक समबाहु त्रिभुज के आकार की कॉयल $($ भुजा $=i )$ को चुम्बक के ध्रुवों के बीच लटकाया गया। चुम्बकीय क्षेत्र $\overrightarrow{ B }$ कायॅल के समतल में है। कायॅल में धारा का मान $i$ हो तो आघूर्ण $(\tau)$ होगाView Solution
- 79दो चुम्बक जिसका चुम्बकीय आघूर्ण $M$ तथा $2 M$ है, एक वाईब्रेशन मैग्नेटोमीटर में रखी है। यदि दोनों के सम ध्रुव साथ हो तो आवर्तकाल $T_1$ तथा विषम ध्रुव साथ हो तो आर्वत काल $T_2$ है। तो$-$View Solution
- 80एक कुँडली जिसका क्षेत्रफल $A$ तथा फरों की संख्या $N$ है में धारा $i$ प्रवाहित होती हो। उसका चुम्बकीय आघूर्ण-View Solution
- 81एक चुम्बक जिसका चुम्बकीय आघूर्ण $\vec{M}$ है, उसे चुम्बकीय क्षेत्र तीव्रता $\overrightarrow{ B }$ में रखा है। तो बल आघूर्ण है:View Solution
- 82एक प्रतिचुम्बकीय पदार्थ को छड़ चुम्बक के $N$ तथा $S$ ध्रुवों के पास लाने पर वहView Solution
- 83View Solutionकिसी एक नाजुक उपकरण को बाहय विद्युत क्षेत्र से बचाने के लिए:
- 84एक चुम्बक जिसका चुम्बकीय आघूर्ण $M$ को $90^{\circ}$ से घुमाने में किया गया, $60^{\circ}$ घुमाने में किये कार्य से $n$ गुना ज्यादा है तो $n$ का मान:View Solution
- 85एक छड़ चुम्बक पृथ्वी के चुम्बकीय क्षेत्र में आवर्तकाल $T$ से दोलन करती है। यदि चुम्बक का द्रव्यमान $1 / 4$ कर दे तो आवर्तकाल:View Solution
- 86किसी लम्बी परिनालिका में फेरों की संख्या $1000$ है। जब परिनालिका से $4 A$ धारा प्रवाहित होती है, तब इस परिनालिका के प्रत्येक फेरे से संबद्ध चुम्बकीय फ्लक्स $4 \times 10^{-3} Wb$ है । इस परिनालिका का स्व$-$प्रेरकत्व है:View Solution
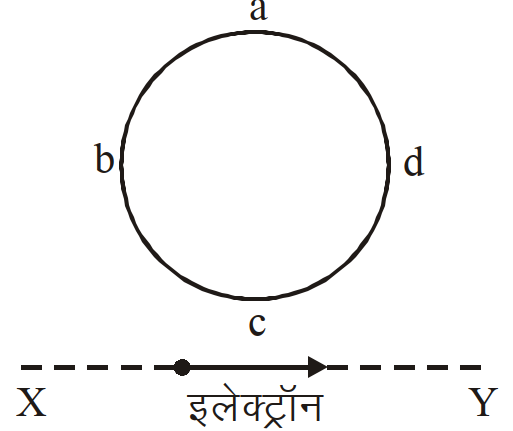
- 87एक इलेक्ट्रॉन सरल रेखीय पथ, $XY$ पर गतिमान है। एक कुंडली abcd इस इलेक्ट्रॉन के मार्ग के निकटवर्ती है (आरेख देखिये) तो, इस कुंडली में प्रेरित धारा (यदि कोई हो तो) की दिशा क्या होगी?View Solution
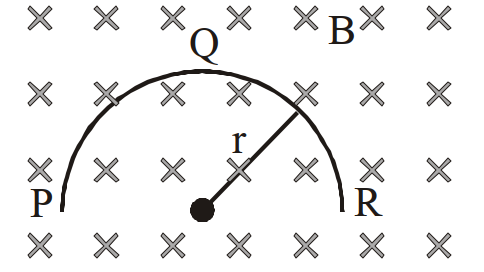
- 88$r$ त्रिज्या की एक पतली अर्द्धवृत्ताकार चालक रिंग (वलय) $( PQR )$ किसी क्षैतिज चुम्बकीय क्षेत्र $B$ में गिर रही है। गिरते समय इसका समतल, आरेख में दर्शाये गये अनुसार, ऊध्र्वाधर रहता है। जब गिरती हुई रिंग की चाल $v$ है तो, इसके दो सिरों के बीच विकसित विभवान्तर होगाView Solution
- 89View Solutionतार का एक पाश (लूप) किसी चुम्बकीय क्षेत्र में घूर्णन करता है तो एक परिक्रमण (चक्र) में इसमें प्रेरित ई.एम. एफ. (e.m.f.) की दिशा में परिवर्तन की आवृत्ति होती है:
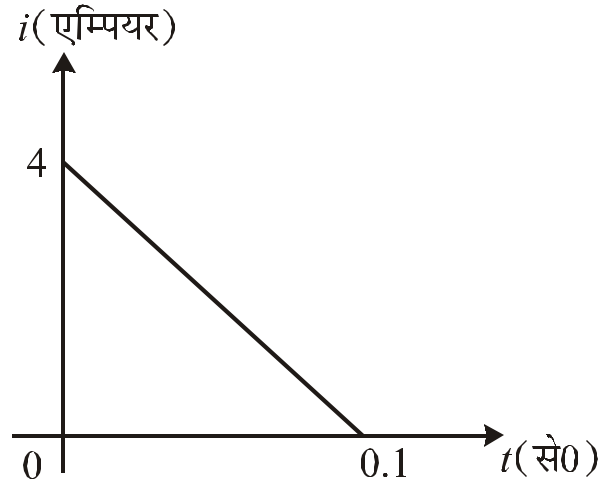
- 90$10 \Omega$ प्रतिरोध की एक कुंडली में, इससे संबद्व चुम्बकीय फ्लक्स के परिवर्तन से प्रेरित विधुत धारा को समय के फलन के रूप में दिये गए आरेख द्वारा प्रदर्शित किया गया है तो, इस कुंडली से संबद्व फ्लक्स में परिवर्तन का मान वेबर में है:View Solution
- 91$400 \Omega$ प्रतिरोध की एक कुंडली को एक चुम्बीय क्षेत्र में रखा गया है। यदि कुंडली से संबद्ध चुम्बकीय फ्लक्स $\phi( wb )$ समय $t$ ( सेकंड) के साथ निम्न प्रकार परिवर्तित होता है, $\phi=50 t ^2+4$ तो कुण्डली में प्रवाहित धारा ( जब $t=2$ सेकंड) होगी:View Solution
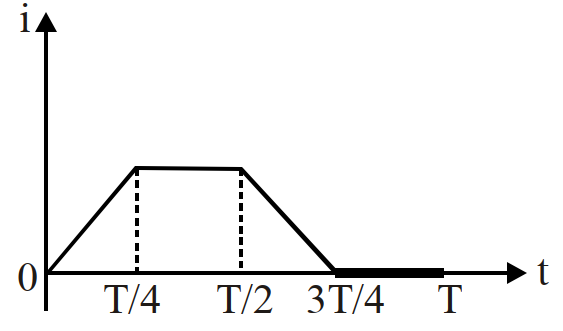
- 92किसी कुण्डली में विद्युतधारा $i$ का मान आरेखानुसार समय के साथ परिवर्तित होता है, तो प्रेरित विद्युत वाहक बल का मान समय के साथ परिवर्तित होगा:View Solution
- 93एक चालक वृताकार पाश ( लूप) को किसी एकसमान चुम्बकीय क्षेत्र में रखा गया है। चुम्बकीय क्षेत्र की तीव्रता $B=.025 T$ है और इसका तल पाश के लम्बवत् है। पाश की त्रिज्या को $1 mm s ^{-1}$ की स्थिर दर से सिकुड़ने दिया जाता है। पाश की त्रिज्या 2 सेमी होने पर उसमें प्रेरिज विद्युत वाहक बल (e.m.f.) हैView Solution
- 94एक आयताकार, एक वर्गाकार, एक वृत्तीय और एक दीर्घवृत्तीय फन्द जो सभी $x - y$ तल में हैं, एक अचर चुम्बकीय क्षेत्र से स्थिर वेग $\overrightarrow{ V }= v \hat{ i }$ से बाहर निकल रहे हैं। चुम्बकीय क्षेत्र की दिशा ऋणात्मक $z$ अक्ष की दिशा में है। क्षेत्र से बाहर निकलने के प्रक्रम में इन फन्दों में प्रेरित वि.वा.ब (emf) स्थिरमानी नहीं रहेगा :-View Solution
- 95एक चालक वृत्तीय फंद को $0.04 T$ के अचर चुम्बकीय क्षेत्र में इस तरह रखा है कि फंद का तल चुम्बकीय क्षेत्र की दिशा से लम्ब दिशा में है। फन्द् की त्रिज्या $2 mm / s$. की दर से घटने लगती है। जब फन्द की त्रिज्या $2 cm$ होगी तो इसमें प्रेरित वि.वा.ब. $( emf )$ का मान होगा:-View Solution
- 96एक लम्बे बहुकुंडलक(सोलिनाइड) में 500 फेरें हैं। जब इसमें 2 ऐम्पीयर की धारा प्रवाहित की जाती है, तो हर फेरे से सम्बन्धित चुम्बकीय फ्लक्स $4 \times 10^{-3} Wb$ होती है। सोलिनाइड का स्वप्रेरकत्व होगा:View Solution
- 97दो कुण्डलियों के स्वप्रेरण $2 mH$ तथा $8 mH$ हैं। दोनों को इतना नजदीक रखा गया कि पहली कुण्डली का चुम्बकीय फ्लक्स दूसरी से भी लिंक हो सके। तो इनके बीच अन्तः प्रेरण है :View Solution
- 98दिये गये चित्र में यदि चुम्बकीय फ्लक्स परिवर्तन कराया जाए $V$ वोल्ट का वि.वा. बल बनता है। एक आवेश $Q$ को लूप पर घुमाने में किया गया कार्य है :View Solution
- 99एक परिपथ जिसका प्रतिरोध $R$ है उसमें लगने वाला चुम्बकीय फ्लक्स $\Delta \phi, \Delta t$ समय में बदल जाता है तो परिपथ में बनने वाला कुल आवेश $Q , \Delta t$ समय में है:View Solution
- 100एक स्वप्रेरण $L =2 mH$ में धारा $i = t ^2 e ^{- t }$ से परिवर्तित होता है। किस समय वि.वा.ब. का मान शून्य होगा:View Solution