Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1निम्न समीकरणों में से कौन सी सरल आवर्ती चाल की सूचक है:- (जबकि $k , k _0, k _1$ और $a$ सभी, धनमानी हैं।)View Solution
- 2एक सरल लोलक $x=0$ के परित: सरल आवर्ती चाल से चल रहा है जिसका आयाम $a$ और समय अन्तराल $T$ है। $x =\frac{ a }{2}$ पर लोलक की चाल होगी :-View Solution
- 3दो सरल आवर्त गतियाँ जिनकी कोणीय आवृतियाँ $100$ और $1000$ रैडियन प्रति सेकेण्ड हैं, समान विस्थापन आयाम रखती हैं। उनके अधिकतम त्वरणों का अनुपात होगा :View Solution
- 4एक बिन्दु सरल आवर्त दोलन करता है जिसका आवर्तकाल $T$ और चलन का समीकरण $x = a \sin (\omega t +\pi / 6)$ है। आवर्तकाल के किस अंश के पश्चात् बिन्दु का वेग उसके अधिकतम वेग का आधा होगा ?View Solution
- 5एक कण सरल आवर्ती गति में है। इसके तात्क्षणिक वेग और त्वरण का कलान्तर होगा $-$View Solution
- 6एक कण आयाम $a$ के साथ सरल आवर्ती दोलन करता है। इसका दोलनकाल $T$ है। इस कण को अपनी साम्य अवस्था से आयाम की आधी दूरी चलने में लगने वाला कम से कम समय होगा $-$View Solution
- 7एक कण सरल आवर्ती गति में है। इसकी गतिज ऊर्जा $K _0 \cos ^2 \omega t$ है। इसकी स्थितिज ऊर्जा और सम्पूर्ण ऊर्जा के क्रमानुसार अधिकतम मान होंगे $-$View Solution
- 8एक ऊर्ध्व दिशा की कमानी को धरातल पर चित्र के अनुसार स्थायी किया गया है तथा इसके ऊपरी सिरे के पलड़े पर $2.0$ किग्रा द्रव्यमान की वस्तु रखी है। कमानी और पलड़े के भार नगण्य हैं। थोड़ा दबाकर छोड़ देने पर द्रव्यमान सरल आवर्ती गति करता है। कमानी का बल नियतांक 200 न्यूटन/मी है। आवर्त गति का न्यूनतम आयाम कितना होना चाहिए, जिससे ऊपर रखी वस्तु पलड़े से अलग हो जाये?( मान लो $g =10$ मी $/$ से $^2$ )View Solution

- 9जब एक लम्बे स्प्रिंग को $2$ सेमी खींचा जाता है तो इसमें संचित स्थितिज ऊर्जा $U$ होती है। यदि इसे $8$ सेमी खींचा जाए तो इसमें संचित स्थितिज ऊर्जा होगी:View Solution
- 10$5$ सेमी आयाम की सरल आवर्त गति करते एक कण की अधिकतम चाल $31.4$ सेमी./से है। इसके कम्पन की आवृत्ति हैView Solution
- 11सरल आवर्त गति करते एक कण की चाल $v$ तथा त्वरण $a$ के लिए, तिम्नलिखित में से कौन $-$ सा कथन सत्य है?View Solution
- 12बल नियतांक $k _1$ व $k _2$ वाली दो स्प्रिंगो को श्रेणी क्रम में जोड़ा गया है। संयोग का प्रभावी बल नियतांक है:View Solution
- 13View Solutionएक सरल आवर्त गतिक कम्पक की स्थितिज ऊर्जा कितनी होगी, जब कण अपने अंत्य बिंदु के आधे रास्ते पर है:
- 14एक स्प्रिंग से लटके द्रव्यमान का आवर्तकाल $T$ है। यदि स्प्रिंग को चार बराबर भागों में बांट दिया जाए व समान द्रव्यमान को किसी एक भाग से लटकाये तो आवर्तकाल होगा :View Solution
- 15द्रव्यमान $m$ का एक कण दो बिन्दुओं $x _1$ व $x _2$ के बीच सरल आवर्त गति में कम्पन करता है, साम्य स्थिति $O$ है, तो इसकी स्थितिज ऊर्जा का ग्राफ होगा:View Solution
- 16एक कण आयाम ' $a$ ' से सरल आवर्तगति करता है। इसकी स्थिति ऊर्जा अधिकतम होगी जब यह माध्य स्थिति से दूर होगाView Solution
- 17एक सरल लोलक का आयाम वास्तविक आयाम का $1 /$ 3 भाग हो जाता है जब वह 100 दोलन पूरे कर लेता है। जब वह 200 दोलन पूरे कर लेता है तो उसका आयाम $S$ भाग हो जाता है जहां $S$ का मान होगा-View Solution
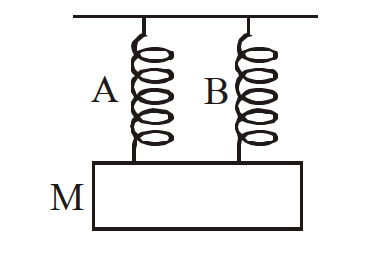
- 18एक $m$ द्रव्यमान का पिण्ड ऊर्ध्वाधरत सरल: आवर्तगति करता है। जब द्रव्यमान को स्प्रिंग $A$ से लटकाया जाता है तो उसका आवर्तकाल $t_1$ तथा $B$ से लटकाने पर आवर्तकाल $t _2$ है। यदि $A$ तथा $B$ को दिये गये चित्र की तरह जोड़ा जाए तो आवर्तकाल $t _0$ दिया जाता हैView Solution
- 19एक कण $m$ द्रव्यमान का है। वह ' $a$ ' आयाम की सरल आवृतगति करता है। उस पर $F =- kx$ का बल लगता है। कण की कुल ऊर्जा किस पर निर्भर करेगी?View Solution
- 20View Solutionएक सरल लोलक में एक धातु का लोलक इस्तेमाल किया गया है जो ऋणावेशित है। यह एक धनावेशित प्लेट के ऊपर दोलन करता है। तो इसका आवर्तकाल
- 21दो द्रव्यमान $M _{ A }$ तथा $M _{ B }$ को दो तारों, जिनकी लम्बाइयां $L _{ A }$ तथा $L _{ B }$ है, से लटकाने पर सरल आवर्तगतियां करते है। यदि इनकी आवर्तियों में संबंध $f _{ A }=2 f _{ B }$ हो तोView Solution
- 22एक कण पर दो सरल आवर्तगतियां है। ये है$x = A \cos (\omega t +\delta) ; y = A \cos (\omega t +\alpha)$ जब $\delta=\alpha+\frac{\pi}{2}$, तो परिणामी गति होगी $-$View Solution
- 23View Solutionएक सरल लोलक का आवर्तकाल 2 सेकंड है। यदि इसका लम्बाई 4 गुणा कर दी जाए तो इसका आर्वतकाल होगा
- 24एक कण $0.01$ मीटर आयाम तथा $60$ हर्टज आवृत्ति की सरल आवर्तगति करता है। कण का अधिकतम त्वरण होगा :View Solution
- 25यदि सरल लोलक की लम्बाई $2 \%$ बढ़ा दी जाए तो उसका आवर्तकालView Solution
- 26View Solutionएक खोखले गोले में पानी भरा गया है। इसे एक लम्बे धागे से लटकाया गया है। गोले की तली में एक छेद है तो दोलनकाल
- 27दो सरल लोलकों की लम्बाई $5$ मीटर तथा $20$ मीटर है। इनमें छोटा सरल रेखीय विस्थापन एक ही समय तथा एक ही दिशा में है। ये फिर एक ही कला में होंगे जब छोटी लम्बाई वाले लोलक ने $.......$ दोलन पूरे करे?View Solution
- 28दो सरल आवृत्तगति एक दूसरे के लम्बवत् है अर्थात् एक $x - $ अक्ष में तथा दूसरा $y-$ अक्ष में है। यदि दोनों का आयाम समान तथा कलान्तर $\pi / 2$ हो तो पथ होगा $-$View Solution
- 29View Solutionएक सरल आवृत्ति गति में जब विस्थापन आयाम का चौथाई होता है तो बताओ कुल ऊर्जा का कितना भाग गतिज ऊर्जा होगा?
- 30एक सरल आवृर्त्त दोलनचित्र में बल नियतांक $2 \times 10^6$ न्यूटन/मीटर, आयाम $0.01$ मीटर तथा कुल ऊर्जा $160 J$ है; तोView Solution
- 31एक कण अपनी माध्य स्थिति में सरल आवृत्त गति करता है। इसका आयाम $A$ तथा आवर्तकाल $T$ है। जब उसका वेग अधिकतम वेग का आधा हो तो उस समय विस्थापन ज्ञात करो:View Solution
- 32एक कण दो परस्पर लम्बवत् सरल आवर्त गतियाँ इस प्रकार करते हैं कि इसके $x$ तथा $y$ अक्ष इस प्रकार दिये जाते है : $x =2 \sin \omega t ; \quad y =2 \sin A \left(\omega t +\frac{\pi}{4}\right)$ कण का पथ होगाView Solution
- 33View Solutionनिम्न में से कौन-सी गति सरल आवर्तगति होगी
- 34एक कण आयाम $A$ के साथ सरल आवर्तगति करता है। माध्य स्थिति से कितनी दूरी पर उसकी स्थितिज ऊर्जा कुल ऊर्जा की एक चौथाई है ?View Solution
- 35सरल आवर्तगति करते हुए पिण्ड का विस्थापन $0.2$ मीटर हो तो उसका त्वरण 2 मी/सेकंड 2 होता है। इसकी कोणीय आवृत्ति होगी-View Solution
- 36एक सरल आवर्तगति करते हुए कण का आयाम $A$ तथा आवर्तकाल $T$ है। $x = A$ से $x = A / 2$ तक चलने में लगा समय होगा$-$View Solution
- 37एक पिण्ड सरल आवर्तगति करता है। जब उसका विस्थापन माध्य स्थिति से $4$ सेमी तथा $5$ सेमी हो तो उसका वेग $10$ सेमी/सेकंड तथा $8$ सेमी/सेकंड है, इसका आवर्तकाल होगा $-$View Solution
- 38एक सरल लोलक एक क्षैतिज दिशा में ' $a$ ' त्वरण से चलती हुई ट्राली की छत से लटका है। उसका आवर्तकाल $T =2 \pi \sqrt{\frac{\ell}{ g }}$ से दिया जाता है जहां $g$ का मान होगाView Solution
- 39एक सरल लोलक का आयाम तथा कोणीय वेग क्रमशः $a$ तथा $\omega$ है। माध्य स्थिति से $x$ दूरी पर इसकी गतिज ऊर्जा $T$ तथा स्थितिज ऊर्जा $V$ है तो $T$ तथा $V$ का अनुपात होगाView Solution
- 40एक $m$ द्रव्यमान की वस्तु श्रेणीक्रम में जुड़ी हुई $K _1$ और $K _2$ बल नियतांको की स्प्रिंगो से लटकी हुई है। वस्तु का दोलनकाल होगा-View Solution
- 41समान आवर्तकाल, एक दूसरे से $90^{\circ}$ के कोण पर तथा $\pi$ कलान्तर की दो सरल आवर्तगतियों के संयोजन से कण का विस्थापन होता है-View Solution
- 42एक कण पर रेस्टोरिंग बल उसके विस्थापन के समानुपाती है तथा घर्षण बल उसके वेग के समानुपाती है जबकि उस पर $F \sin \omega t$ का बल कार्य करता है। यदि कण का आयाम $\omega=\omega_1$ पर अधिकतम हो तथा कण की ऊर्जा $\omega=\omega_2$ पर अधिकतम हो तोView Solution
- 43एक कण $X$-अक्ष की दिशा में चलता हुआ सरल आवृत गति करता है तो बल होगाView Solution
- 44द्रव्यमान $m _1$ तथा लम्बाई $L$ की कोई एकसमान रस्सी किसी दृढ़ टेक से ऊध्धाधर लटकी है। इस रस्सी के मुक्त सिरे से द्रव्यमान $m _2$ का कोई गुटका जुड़ा है। रस्सी के मुक्त सिरे पर तरंगदैर्घ्य $\lambda_1$ का कोई अनुप्रस्थ स्पन्द उत्पत्र किया जाता है। यदि रस्सी के शीर्प तक पहुँचने पर इस स्पन्द की तरंगदैर्घ्य $\lambda_2$ हो जाती है, तब अनुपात $\lambda_2 / \lambda_1$ का मान है :View Solution
- 45View Solutionएक सिरे पर बन्द तथा दूसरे सिरे पर खुला कोई वायु स्तम्भ किसी स्वरित्र द्विभुज के साथ उस समय अनुनाद करता है जब इस वायु स्तम्भ की कम-से-कम लम्बाई 50 सेमी. होती है। इसी स्वरित्र द्विभुज के साथ अनुनाद करने वाली स्तम्भ की अगली बड़ी लम्बाई है
- 46$800 Hz$ आवृत्ति की ध्वनि उत्पत्र करने वाला कोई सायरन किसी प्रेक्षक से एक चट्टान की ओर $15 \ ms ^{-1}$ की चाल से गतिमान है । तब उस ध्वनि की आवृत्ति, जिसे चट्टान से परावर्तित प्रतिध्वनि के रूप में वह प्रेक्षक सुनता है, क्या होगी? $($वायु में ध्वनि की चाल $=330 \ ms ^{-1}$ लीजिए$)$View Solution
- 47एक डोरी दो स्थिर बिन्दुओं के बीच खिची है। इन बिन्दुओं के बीच की दूरी $75.0 cm$ है। इस डोरी की दो अनुनाद आवृत्तियाँ $420 Hz$ तथा $315 Hz$ है। इन दोनो के बीच में कोई अन्य अनुनाद आवृत्ति नहीं है, तो इस डोरी के लिए न्यूनतम अनुनाद आवृत्ति हैView Solution
- 48ट्रैफिक जैम के कारण एक मोटर साइकिल चालक अपनी चाल कम करते हुए उसे $36$ किमी प्रति घण्टे कर देता है। ट्रैफिक कम होने पर, उससे आगे $18$ किमी प्रति घण्टे की चाल से चलती हुई एक कार$, 1392$ हर्ट्ज आवृत्ति का हॉर बजाती है। यदि ध्वनि की चाल $343$ मी/ से है तो, मोटर साइकिल चालक को इस हॉर्न की आवृत्ति सुनाई देगीView Solution
- 49यदि वायु में ध्वनि का वेग $340$ मी/से हो तो $,1250$ हर्ट्ज से कम आवृत्ति वाले 85 सेमी लम्बे एक सिरे पर बन्द नलिका $($पाइप$)$ में वायु $-$ स्तम्भ के संभव प्राकृतिक दोलनों की संख्या होगीView Solution
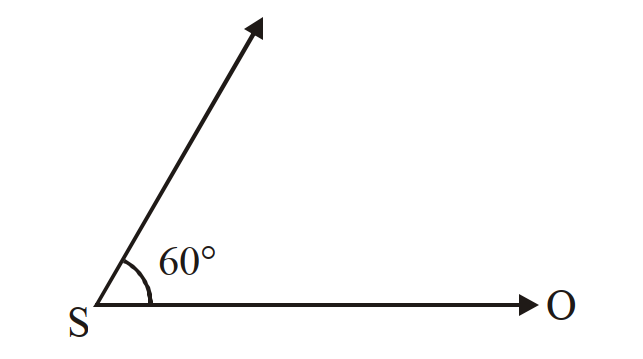
- 50$100 Hz$ आवृत्ति की ध्वनि उत्पन्न करता हुआ एक ध्वनि स्त्रोत $S$ तथा एक प्रेक्षक $O$, एक दूसरे से कुछ दूरी पर स्थित हैं। यह ध्वनि स्त्रोत, $19.4 \ ms ^{-1}$ की चाल से चल रहा है। उसके चलने की दिशा, स्त्रोत तथा प्रेक्षक की रिथितियों को मिलाने वाली सरलरेखा से $60^{\circ}$ का कोण बनाती है $($आरेख देखिये$)$। यदि, प्रेक्षक अपनी रिथति पर ही रूका रहता है तो, प्रेक्षक द्वारा सुनी गई ध्वनि की आभासी आवृत्ति होगी (हवा में ध्वनि का वेग $\left.330 \ ms ^{-1}\right)$ :View Solution
- 51यदि किसी रस्सी को तीन खंडों में विभाजित करने पर उन खंडों की मूल आवृत्तियां क्रमश: $n _1, n _2$ तथा $n _3$ हों, तो इस रस्सी की प्रारम्भिक मूल आवृति $n$ के लिए सम्बन्ध होगाView Solution
- 52अज्ञात आवृत्ति का एक स्रोत, $250 Hz$ आवृत्ति के किसी अन्य स्रोत के साथ प्रति सेकंड 4 विस्पन्द उत्पन्न करता है। अज्ञान आवृत्ति का दूसरा संनादी ( हारमोनिक0), 513 $Hz$ आवृत्ति के स्रोत के साथ 5 विस्पन्द प्रति सेकन्ड उत्पन्न करता है। तो, अज्ञात आवृत्ति है:View Solution
- 53View Solutionदोनों सिरों पर खुले पाइप में कम्पनों के लिए कौन-सा कथन सही नहीं है ?
- 54किसी स्थिर वस्तु की ओर $220 ms ^{-1}$ की चाल से चलती हुई एक ट्रेन $1000 Hz$ आवृत्ति की ध्वनि उत्पन्न करती है। इस ध्वनि का कुछ भाग उस वस्तु से टकराकर प्रतिध्वनि के रूप में वापस आ जाता है। ट्रेन के ड्राइवर द्वारा संसूचित (प्राप्त) इस प्रतिध्वनि की आवृत्ति होगी : (ध्वनि की वायु में चाल $330 ms ^{-1}$ )View Solution
- 55एक दूसरे के निकट स्थित ध्वनि के दो स्त्रोंतों निम्न प्रकार निरूपित प्रगामी तरंगें उत्सर्जित कर रहे है : $y_1=4 \sin 600 \pi t$ तथा $y_2=5 \sin 608 \pi t$. इन दोनों स्त्रोतों के निकट स्थित एक श्रोता को सुनाई देगा :View Solution
- 56किसी स्ट्रिंग (डोरी) को $\ell_1, \ell_2$ तथा $\ell_3$ लम्बाई के तीन भागों में विभाजित करने पर उनकी मूल आवृत्तियाँ क्रमश: $v_1, v_2$ तथा $v_3$ हैं तो, स्ट्रिंग की मूल आवृत्ति होगी:View Solution
- 57किसी प्यानों के दो सर्वसम तारों का तनाव भी समान है और उसका मान $T$ है। इसकी मूल आवृत्ति $600 Hz$ है। यदि दोनों तारों के एक साथ कम्पन करने पर 6 विस्पंद प्रति सेकण्ड बने, तो तारों के तनाव में भिन्नात्मक वृद्धि होगी:View Solution
- 58ध्वनि की तरंगे गर्म वायु में $350 m / s$ की चाल से तथा पीतल में $35000 m / s$ की चाल से चलती है, तो $700 Hz$ की ध्वनिक तरंग यदि गरम वायु से पीतल में प्रवेश करे तो उसकी तरंगदैर्ध्य:View Solution
- 59$512 Hz$ आवृति का एक स्वरित्र द्विभुज, किसी प्यानो के कम्पमान तार के साथ प्रति सेकंड 4 विस्पन्द उत्पन्न करता है। प्यानो के तार पर थोड़ा सा तनाव बढ़ाने पर विस्पन्दों की आवृति 2 प्रति सेकंड हो जाती है। तनाव बढ़ाने से पहले प्यानो के तार की आवृति थीView Solution
- 60किसी अनुप्रस्थ तरंग को $, y = A \sin \ ( wt - kx )$ से निरूपित किया जाता है। तरंगदैध्य के किस मान के लिये तरंग $-$ वेग, अधिकतम कण $-$ वेग के बराबर होगा?View Solution
- 61दो डोरियों की लम्बाइयाँ $51.6 \ cm$ और $49.1 \ cm$ हैं और इनमें से प्रत्येक में पृथक$-$पृथक $20 N$ बल का तनाव कार्य करता है। दोनों डोरियों का प्रति मात्रक लम्बाई द्रव्यमान समान है और यह $1 g / m$. है। जब एक ही समय दोनों डोरियाँ साथ$-$साथ कम्पन करती हैं तो स्पन्दन संख्या होगी $:-$View Solution
- 62एक डोरी में चलती तरंग का आयाम $2 \ cm$ है। यह तरंग $x-$ अक्ष की धन दिशा में $128 m / \sec$. की चाल से चल रही है और यह पाया गया है कि डोरी की $4 m$ की लम्बाई में $5$ पूरी तरंगें समा जाती हैं। तरंग सूचक समीकरण होगा:$-$View Solution
- 63एक कार $30$ मीटर/सेकण्ड की चाल से एक पहाड़ी की ओर चल रही है। उसका चालक $600\ Hz$ आवृत्ति का हार्न बजाता है। यदि वायु में ध्वनि की चाल $330$ मीटर/सेकण्ड हो तो चालक द्वारा सुनी गई परावर्तित ध्वनि की आवृत्ति होगीView Solution
- 64$I _1$ और $I _2$ तीव्रताओं की दो आवर्ती तरंगें एक स्थानसे एक ही समय एक ही दिशा में गुजरती हैं। अधिकतम और न्यूनतम तीव्रताओं का जोड़ होगा :View Solution
- 65$y =0.25 \sin \ (10 \pi x -2 \pi t )$ समीकरण जिसमें $x$ और $y$ मीटरों में है और $t$ सेकण्ड में है, उस तरंग को व्यक्त करता है जिसका गतिपथ है:View Solution
- 66एक कक्ष $A$ का रिभरवेरेशन काल एक सेकण्ड है। एक दूसरे कक्ष के सभी माप कक्ष $A$ की तुलना में दोगुने मान रखते हैं। इस दूसरे कक्ष का रिभरवेरेशन काल (सेकण्ड में) क्या होगा ?View Solution
- 67View Solutionनिम्न में कौन-सा कथन यथार्थ है?
- 68क्रमशः $5.0$ मी और $5.5$ मी तरंगदैर्ध्य की दो ध्वनि तरंगें 330 मी/से के वेग से एक गैस में चल रही है। हम आशा कर सकते हैं कि प्रति सेकण्ड विस्पन्दों की संख्या होगी:View Solution
- 69$x$-अक्ष के साथ चल रही एक अनुप्रस्थ तरंग को निम्न समीकरण द्वारा व्यक्त किया जा सकता है: $ y ( x , t )=8.0 \sin \left(0.5 \pi x -4 \pi t -\frac{\pi}{4}\right) $ जहाँ $x$ का मान मीटर में और $t$ का सेकण्ड में है। इस तरंग की चाल होगी:View Solution
- 70दो कम्पित स्वरित्र प्रगामी तरंगें उत्पन्न करते हैं जो क्रमशः हैं $y _1=4 \sin 500 \pi t$ और $y _2=2 \sin 506 \pi t$. प्रति मिनट उत्पन्न विस्पंदों की संख्या है:View Solution
- 71एक बिन्दु स्रोत अवशोषण रहित माध्यम में सभी दिशाओं में समान रूप से ध्वनि उत्पन्न करता है। दो बिन्दु $P$ और $Q$ स्रोत से क्रमशः 2 मीटर तथा 3 मीटर दूरियों पर है। बिन्दुओं $P$ व $Q$ पर तंरगों की तीव्रताओं का अनुपात है:View Solution
- 72एक कार एक ऊँची चोटी की ओर गति कर रही है। कार चालक आवृत्ति $f$ का हार्न बजाता है। चालक द्वारा सुनी गयी परावर्तित ध्वनि की आवृत्ति $2 f$ है। यदि ध्वनि का वेग $v$ है, तो समान मात्रक में कार का वेग होगा:View Solution
- 73निम्नलिखित दो तरंगों $ y _1=10^{-6} \sin \{100 t+( x / 50)+0.5\} m$View Solution
$y _2=10^{-6} \cos \{100 t+( x / 50)\} m $ के बीच कलान्तर जहाँ $x$, मीटर में तथा $t$ सेकण्ड में है, लगभग है: - 74एक प्रेक्षक ध्वनि की वेग की $1 / 5$ वेग से स्थिर स्रोत की ओर बढ़ रहा है। स्रोत द्वारा उत्पन्न ध्वनि की तंरगदैर्ध्य व आवृत्ति क्रमशः $\lambda$ और $f$ है। प्रेक्षक द्वारा प्रेक्षित आभासी तरंगदैर्ध्य व आवृत्ति होगी:View Solution
- 75View Solutionप्रणोदित दोलनों की स्थिति में, अनुनादी तरंग बहुत तीव्र हो जाती है, जब:
- 76एक आगामी तरंग $x-$ अक्ष की धनात्मक दिशा में चलती है। इसका आयाम $0.2\ m$, वेग $360$ मी/सेकंड तथा तंरदैर्ध्य $60\ m$ है। इसकी समीकरण होगी $-$View Solution
- 77एक सीटी की आवृत्ति $385$ हर्टज है इसे $50$ सेमी त्रिज्या के क्षैतिज वृत्त में $20$ रेडियन/सेकंड के कोणीय वेग से घुमाया जाता है। श्रोता को कितनी न्यूनतम आवृत्ति सुनायी देगी जब वह केन्द्र से अधिकतम दूरी पर हो। हवा में ध्वनि का वेग $340$ मी/सेकंड है।View Solution
- 78एक तरंग $y =10^{-4} \sin \left[100 t -\frac{ x }{10}\right]$ से प्रदर्शित होती है। तरंग का वेग होगा-View Solution
- 79एक तार का द्रव्यमान $0.033$ किग्रा तथा लम्बाई 7 मीटर है। यदि तार में तनाव $60.5 N$ हो तो तरंग का वेग होगाView Solution
- 80एक श्रोता तथा स्रोत एक दूसरे से $100$ मी/सेकंड $($पृथ्वी के सापेक्ष$)$ से दूर जा रहे हैं। यदि श्रोता को स्रोत से निकलने वाली आवृत्ति $1950$ हर्टज सुनायी पड़ती है तो स्रोत की वास्तविक आवृत्ति क्या होगी? $\left( V _{ s }=340\right.$ मी/सेकंड $)$View Solution
- 81दो ध्वनि स्रोत $\lambda$ तरंगदैर्ध्य की ध्वनि निकालते है जबकि ये एक दूसरे से नियत दूरी पर है। एक श्रोता वेग $u$ से दोनों स्रोतों को जोड़ने वाली रेखा पर चलता है। श्रोता को कितनी विस्पंद/सेकन्ड सुनाई देगी?View Solution
- 82यदि एक तार को तीन हिस्सों में बांटे तो उनकी मूल आवृत्तियां $n _1, n _2 \ n _3$ है तथा पूरे तार की मूल आवृत्ति $n$ है तो $-$View Solution
- 83दो तरंग जिनकी लम्बाई $50$ सेमी तथा $51$ सेमी है एक साथ $12$ विस्पंद/सेकन्ड बनाती है तो ध्वनि का वेग होगाView Solution
- 84View Solutionअनुनाद उदाहरण है
- 85एक गाड़ी के हॉर्न की आवृति $n$ है तथा यह श्रोता तथा गाड़ी को जोड़ने वाली रेखा के लम्बवत 30 मी/सेकंड से चलता है। श्रोता को आवृत्ति $n + n _1$ सुनायी देती है (जबकि ध्वनि का वेग हवा में 330 मी./से है) तो-View Solution
- 86एक अनुप्रस्थ तरंग $y = y _0 \sin \frac{2 \pi}{\lambda}( vt - x )$ से प्रदर्शित होती है। $\lambda$ के किस मान के लिए कण का वेग तरंग के वेग का दोगुना होगा?View Solution
- 87एक द्रव्यमान $m$ एक भारहीन स्प्रिंग से ऊधर्व्वाधर लटका है। यह $n$ आवृत्ति से दोलन करता है। इसकी आवृत्ति क्या होगी यदि द्रव्यमान बदलकर $4 \ m$ कर दिया जाए?View Solution
- 88एक ज्या तरंग को अधिकतम विस्थापन से 0 विस्थापन तक जाने में $0.170$ सेकंड लगते है; इसकी आवृति होगीView Solution
- 89एक स्थायी तरंग के दो अणुओं के बीच की दूरी $1.21 Å$ है। यदि उसमें 3 निस्पंद व 2 प्रस्पंद बनते है तो तरंग की तरंग दैर्ध्य होगी:View Solution
- 90एक आगामी तरंग $y =60 \cos (180 t -6 x )$ से प्रदर्शित होती है। जहां $y$ माइक्रॉन $t$ सेकंड व $x$ मीटर में है। अधिकतम कण वेग तथा तरंग वेग का अनुपात होगा$-$View Solution
- 91एक बंद आर्गन पाइप $P _1$ का पहला अधिस्वरक तथा खुले आर्गन पाइप $P _2$ का तीसरा अधिस्वरक अनुनाद में है। $P _1$ तथा $P _2$ की लम्बाईयों का अनुपात होगाView Solution
- 92एक खुले आर्गन पाइप की हवा में मूल आवृति $f$ है। यदि इस पाईप को ऊध्ध्वाधर आधा पानी में डुबो दिया जाए तो इसकी मूल आवृति होगी-View Solution
- 93View Solutionएक माध्यम में तरंग का वेग 960 मी/सेकंड है। यदि किसी बिन्दु से 1 मिनट में 3600 तरंग गुजरती है तो उसकी तरंगदैर्ध्य होगी-
- 94View Solutionदो तरंग समान आवृत्ति तथा समान तीव्रता की है, एक दूसरे के साथ व्यतिकरण करती है। ये एक दूसरे की विपरीत कला में है। व्यतिकरण के बाद तीव्रता तथा आवृत्ति
- 95दो ध्वनि तरंगों के बीच कलान्तर $60^{\circ}$ है तो इनका पथान्तर होगा $-$View Solution
- 96एक तारे में से $5000 \mathring A $ की तरंगे आती है जो पृथ्वी पर $1.50 \times 10^6$ मी/सेकंड से पहुंचती है। पृथ्वी पर पहुंचते हुए इसकी तरंग दैर्ध्य में क्या अंतर होगा?View Solution
- 97View Solutionआर्र्रता बढ़ाने पर ध्वनि तरंगों पर क्या प्रभाव होता है?
- 98एक ध्वनि तरंग की समी. $y =0.0015 \sin (62.4 x +316)$ है। इसकी तरंगदैर्ध्य होगी-View Solution
- 99एक माध्यम में तरंग का वेग $760$ मीटर है। यदि किसी बिन्दु से $2$ मिनट में $3600$ तरंग गुजरती हो तो इसका तरंगदैर्ध्य होगा $-$View Solution
- 100एक अस्पताल में ट्यूमर को जाँचने के लिए अल्ट्रा सोनिक स्कैनर लगाया जाता है। स्कैनर की आवृति $4.2$ $MHZ$ है तथा ध्वनि की आवृत्ति $1.7$ किमी/सेकंड है तो ध्वनि की तरंग दैर्ध्य होगी-View Solution