Question Bank
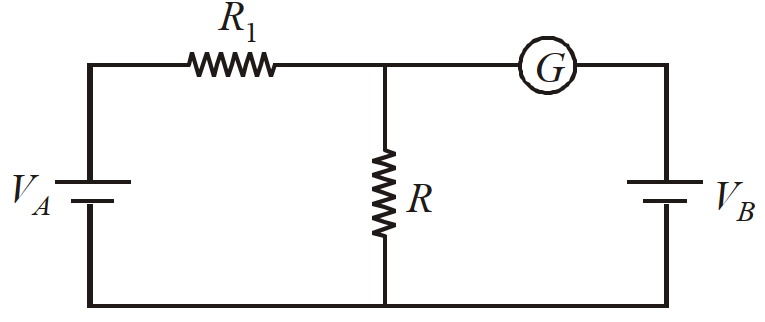
Explore our large set of questions to practice for your standard seamlessly- 1दर्शाये गये परिपथ में दो सेलों $A$ तथा $B$ का प्रतिरोध नगण्य है, जब $V_A=12 V , R_1=500 \Omega$ तथा $R=100 \Omega$ है तो, गैल्वेनोमीटर $(G)$ में कोई विक्षेप नहीं होता है। $V_B$ का मान है :View Solution
- 2एक विद्युत बल्ब की अंकित वोल्टता तथा शक्ति क्रमशः $220$ वोल्ट $- 100$ वॉट है। यदि बल्ब के सिरों के बीच वोल्टता, इस अंकित वोल्टता से $2.5 \%$ कम हो जाये तो, उसकी शक्ति में, अंकित शक्ति के सापेक्ष कितने प्रतिशत की कमी होगी ?View Solution
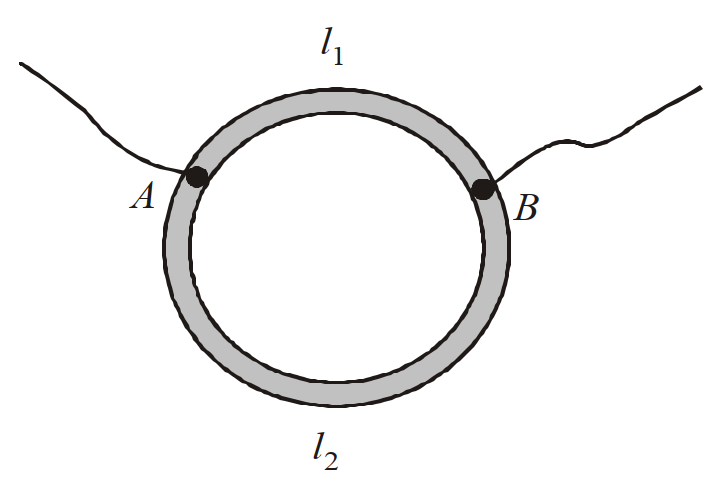
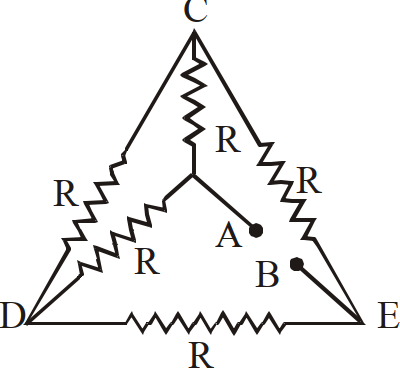
- 3एक वलय, एक तार जिसका प्रतिरोध $R_0=12 \Omega$ से बना है। इस वलय में ऐसे किन दो बिन्दुओं $A$ और $B$ जैसा कि चित्र में दिखाया गया है, पर धारावाही चालक को जोड़ा जाय ताकि, इन दो बिन्दुओं के बीच उप परिपथ का प्रतिरोध $R =\frac{8}{3} \Omega$ हो।View Solution
- 4नगण्य प्रतिरोध का एक ताप-विद्युत युग्म, ताप के रेखीय परिसर में $40 \mu V /{ }^{\circ} C$ विद्युत वाहक बल (ई.एम.एफ) उत्पन्न करता है। इस ताप विद्युत युग्म के साथ 10 ओम प्रतिरोध का एक गैल्वेनोमीटर लगाया गया है, जिसकी सुग्राहिता $1 \mu A / div$ भाग है, तो इस निकाय (तंत्र) द्वारा संसूचित की जा सकने वाले न्यूनतम तापान्तर का मान होगा:View Solution
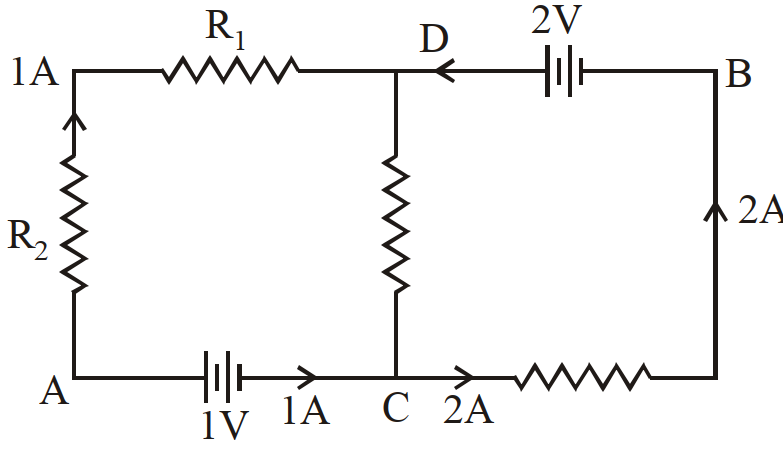
- 5दिखाये गये परिपथ में, यदि बिन्दु $A$ पर विभव को शून्य माना जाये तो बिन्दु B पर विभव होगा:View Solution
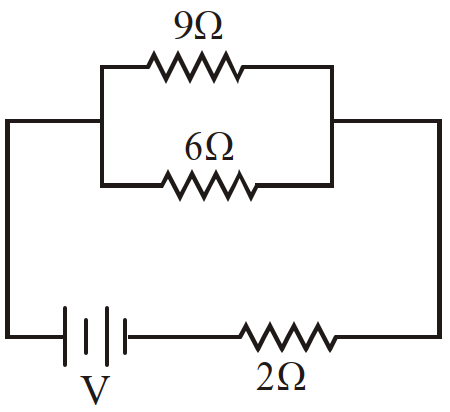
- 6यदि दिये गये परिपथ आरेख में $9 \Omega$ प्रतिरोध में व्यय शक्ति $36$ वाट है, तो $2 \Omega$ प्रतिरोध के सिरों के बीच विभवान्तर होगाःView Solution
- 7किसी बैटरी से जुड़े $2 \Omega$ के प्रतिरोध में $2 A$ विद्युत धारा प्रवाहित होती है। यदि बैटरी $9 \Omega$ के प्रतिरोध में $0.5 A$ की धारा प्रवाहित करती है, तो बैटरी का आंतरिक प्रतिरोध होगा:View Solution
- 8View Solutionकिसी ताप वैद्युत युग्म के उदासीन ताप पर ताप वैद्युत वाहक बल की वृद्धि की दरः
- 9$10^{-2} kg$ द्रव्यमान के किसी कण पर $5 \times 10^{-8} C$ का आवेश है। इस कण को विद्युत क्षेत्र $\bar{E}$ और चुम्बकीय क्षेत्र $\vec{B}$ की उपस्थिति में $10^{-5} ms ^{-1}$ का क्षैतिज वेग दिया जाता है। कण के क्षैतिज दिशा में गति करते रहने के लिये यह आवश्यक है कि (1) $\vec{B}$ वेग की दिशा के लम्बवत् और $\bar{E}$ वेग की दिशा के अनुदिश हो (2) $\vec{B}$ और $\vec{E}$ दोनों ही वेग की दिशा के अनुदिश हो (3) $\vec{B}$ और $\vec{E}$ दोनों आपस में और वेग की दिशा के लम्बवत् हों (4) $\vec{B}$ वेग की दिशा को अनुदिश और $\vec{E}$ उसके लम्बवत् हो निम्नलिखित प्रकथनों के युग्मों में से कौन सा संभव है?View Solution
- 10एक परिनालिका में $2000$ फेरे पास $-$ पास लपेटे गये हैं। इसकी अनुप्रस्थ काट का क्षेत्रफल $1.5 \times 10^{-4} m ^2$ है और इसमें $2.0 A$ की विद्युत धारा प्रवाहित हो रही है। इसे लम्बाई के लम्बवत् अपने केन्द्र से इस प्रकार लटकाया गया है कि यह किसी एकसमान चुम्बकीय क्षेत्र में क्षैतिज समतल में घूम सके। चुम्बकीय क्षेत्र की तीव्रता $5 \times 10^{-2}$ टेसला है और यह परिनालिका के अक्ष से $30^{\circ}$ का कोण बनाता है। परिनालिका पर बल आघूर्ण होगाView Solution
- 11किसी ताप-वैद्युत युग्म का वोल्ट में ताप-विद्युत वाहक बल $E,{ }^{\circ} C$ में दोनों संधियों के बीच तापान्तर $\theta$ पर इस प्रकार निर्भर करता है $E=30 \theta-\frac{\theta^2}{15}$, इस ताप-वैद्युत युग्म का उदासीन ताप होगाView Solution
- 12विद्युतवाही एक लूप $($पाश$)$ में दो एक समान अर्धवृत्ताकार भाग है। प्रत्येक की त्रिज्या $R$ है। एक $x-y$ समतल में और दूसरा $x-z$ समतल में स्थित है। यदि लूप $($पाश$)$ में विद्युत धारा $i$ हो तो, उनके उभयनिष्ठ केन्द्र पर दोनों अर्धवृत्ताकार भागों के द्वारा उत्पन्न परिणामी चुम्बकीय क्षेत्र हैView Solution
- 13View Solutionनिम्नांकित में से कौन से आबंध से ऐसे ठोस का निर्माण होता है जो दृश्य क्षेत्र में प्रकाश को परावर्तित करता है, और जिसकी वैद्युत चालकता ताप के साथ कम होती है तथा जिसका उच्च गलनांक होता है?
- 14विद्युत अपघटन द्वारा क्लोरीन गैस के उत्पादन के लिए $125 V$ पर $100 kW$ शक्ति का उपयोग होता है। प्रति मिनट कितनी क्लोरीन विमुक्त हो रही है? (क्लोरीन का विद्युत रासायनिक तुल्यांक $=0.367 \times 10^{-6} kg / C$ )View Solution
- 15View Solutionनिम्नलिखित दो कथनों पर विचार कीजिये (a) किरचॉंफ का संधि नियम, आवेश-संरक्षण से प्राप्त होता है। (b) किरचॉंफ का पाश (लूप) नियम, उर्जा-संरक्षण से प्राप्त होता है। निम्नांकित में से कौन सा ठीक (सही) है?
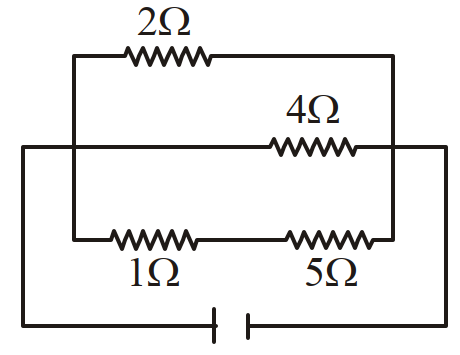
- 16किसी विभवमापी के परिपथ को चित्र में दिखाये गये अनुसार व्यवस्थिति किया गया है। इस विभवमापी के तार पर विभवपात (प्रवणता) $k$ वोल्ट प्रति सेन्टीमीटर है, और जब द्विमार्गी कुंजी नहीं लगी है (आंफ है) तब, परिपथ में जुड़े एमीटर की माप $1.0 A$ है। जब कुंजी (i) 1 और 2 के बीच लगी होती है तो, संतुलन बिन्दु $l_1 cm$ पर, (ii) और जब कुंजी 1 और 3 के बीच लगी होती है तो, संतुलन बिन्दु $l_2 cm$ पर प्राप्त होता है। तो, $R$ और $X$ प्रतिरोधकों का ओम में प्रतिरोध क्रमशः होगाView Solution
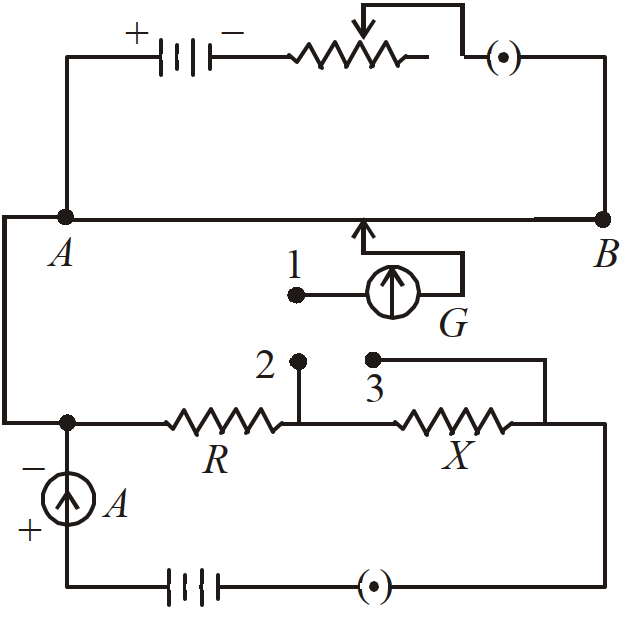
- 17View Solutionचित्र में दिखाये गये वैद्युत परिपथ के सम्बन्ध में निम्न समीकरणों में से कौन सा समीकरण सही है
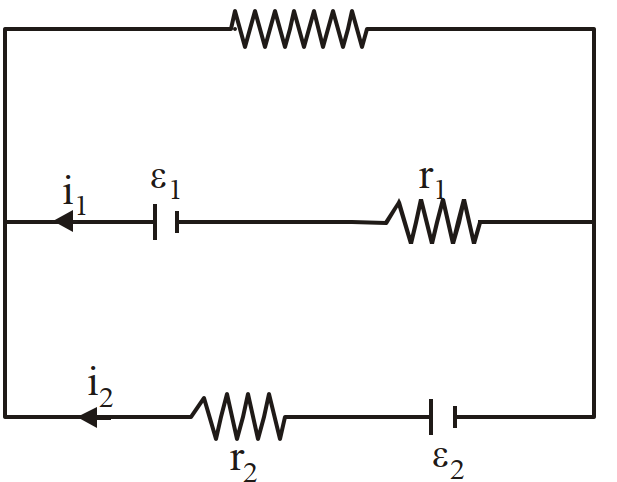
- 1812 ओम प्रति मीटर के एक तार को मोड़ कर 10 से.मी. त्रिज्या का एक वृत्त बनाया गया है। इसके व्यास के अभिमुख बिन्दुओं, $A$ और $B$, जैसा चित्र में दर्शाया हैं, के बीच के प्रतिरोध का मान होगा:-View Solution
- 19एक छात्र एक सैल (जिसका वि.वा.ब. (emf) $E$ है और आन्तरिक प्रतिरोध $r$ है) के टर्मिनलों के विभवांतर (V) का सैल में चल रही धारा (I) से सम्बन्ध जानने के लिए $V$ और I के बीच ग्राफ़ बनाता है। इस ग्राफ की प्रवणता और अंतः खण्ड क्रमानुसार होंगे :-View Solution
- 20इस चित्रित परिपथ के $2 \Omega$ के प्रतिरोध में चलने वाली धारा का मान $3$ ऐम्पीयर है। $5-\Omega$ के प्रतिरोध से शक्ति $($पावर$)$ के क्षय का मान होगा :View Solution
- 21$50 \Omega$ प्रतिरोध के एक गैलवैनोमीटर को $3 V$ की बैट्री से इस तरह जोड़ा गया है कि $2950 \Omega$ का रोधक इससे श्रृंखलाबद्ध जुड़ा है। इस स्थिति में गैलवैनोमीटर में 30 प्रभागों का पूरी स्केल का विक्षेपन होता है। विक्षेपन को 20 प्रभाग का होने के लिए श्रृंखलाबद्ध प्रतिरोध को होना होगा :View Solution
- 22एक पदार्थ विशेष की तार को धीरे $-$ धीरे खींच कर $10 \%$ बड़ा कर लिया गया है। नई अवस्था में इसका प्रतिरोध और विशेष प्रतिरोध क्रमानुसार पहली अवस्था की तुलना में हो जायेंगे :View Solution
- 23एक सैल को पोटैंशियोमीटर तार के $110$ और $100$ से.मी. के प्रति क्रमानुसार $10 \Omega$ के प्रतिरोध से शंटित और न शंटित अवस्था में संतुलित किया जा सकता है। सैल का आंतरिक प्रतिरोध होगा:View Solution
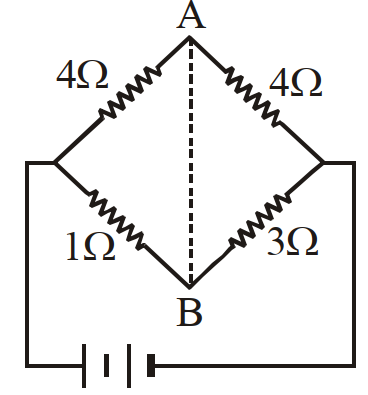
- 24समान मान $2 \Omega$ के तीन प्रतिरोध $P , Q , R$ तथा एक अज्ञात प्रतिरोध $S$ मिल कर व्हीट्स्टोन ब्रिज परिपथ की चार भुजाएँ बनाते हैं। प्रतिरोध $S$ के समान्तर क्रम में $6 \Omega$ का प्रतिरोध लगाने पर ब्रिज संतुलित हो जाता है। अज्ञात प्रतिरोध $S$ का मान कितना है?View Solution
- 25View Solutionइस चित्र में दिखाये गये परिपथ में शक्ति के पूर्ण क्षय का मान (वाट में) होगा-
- 26एक ताम्र वोल्टामीटर में $1.5$ ऐम्पियर की स्थिर धारा 10 मिनट के लिये बहती है। यदि तांबे के लिये विद्युत-रासायनिक तुल्यांक $30 \times 10^{-5}$ ग्राम-कूलाम-1 हो तो इलेक्ट्रोड पर विक्षिप्त ताँबे का द्रव्यमान होगा-View Solution
- 27एक आमीटर का प्रतिरोध $13 \Omega$ है और यह $100$ ऐम्पियर तक की धाराएँ माप सकता है। इसमें अतिरिक्त शंट जोड़ने पर यह आमीटर $750$ ऐम्पियर तक की धाराएँ मापने के लिए सक्षम हो जाता है। अतिरिक्त शंट का प्रतिरोध होगा $-$View Solution
- 28दिये गये चित्र में $A$ तथा $B$ के बीच एक सुचालक तार लगाया गया है। एक तार में प्रवाहित धारा का मान:View Solution
- 29View Solutionकिरचाँफ के नियम :
- 30दो सेल समान वि.वा.ब. तथा $r _1, r _2,\left( r _1> r _2\right)$ आन्तरिक प्रतिरोध के हैं जो बाहय प्रतिरोध $R$ के साथ श्रेणी क्रम में जुड़े है। बंद परिपथ में पहले सेल का विभवांतर शून्य है तो $R$ का मान :View Solution
- 31विद्युत अपघटन के द्वारा क्लोरीन बनाने में $100 W$ की पावर $125 V$ पर खर्च होती है। 1 मिनट में कितनी क्लोरीन बनेगी। क्लोरीन का वैद्युत रासायनिक तुल्यांक (E.C.E.) $0.367 \times 10^{-6}$ किग्रा/कलॉमView Solution
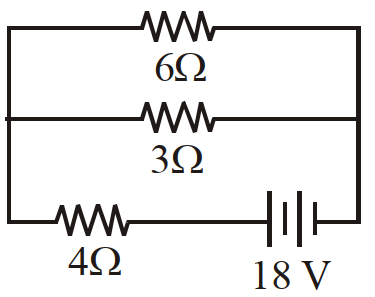
- 32चित्र में $8 \Omega$ प्रतिरोध $2 W$ शक्ति खर्च करता है। $3 \Omega$ प्रतिरोध में कितनी शक्ति खर्च होगी।View Solution
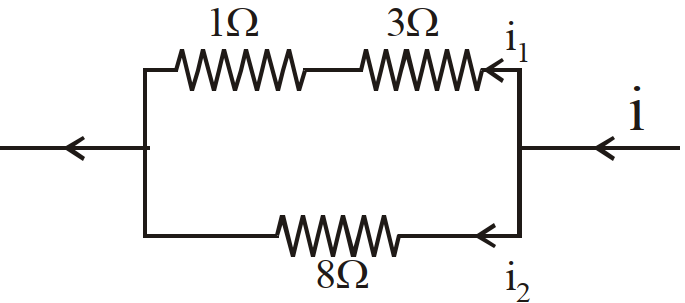
- 33दिये गये परिपथ में धारा $i$ का मान ज्ञात करो।View Solution
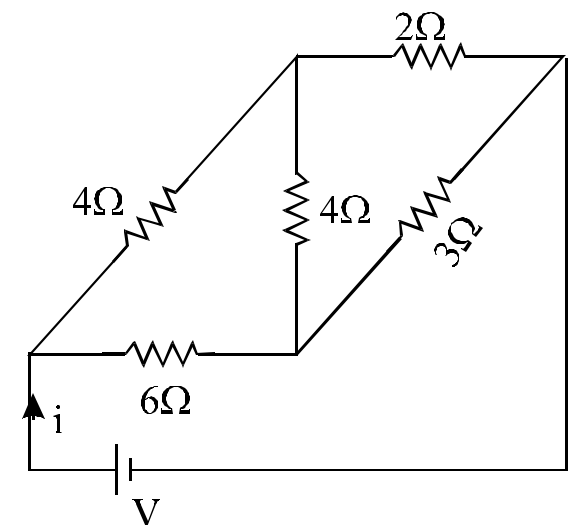
- 34एक तार जिसका वक्र पृष्ठ क्षेत्रफल $a$ लम्बाई 1 तथा प्रतिरोध $R$ है। इसे एक वृत के रूप में मोड़ा गया है। इसके किसी व्यास के दोनों छोड़ो के बीच प्रतिरोध ज्ञात करो।View Solution
- 35एक $5 A$ का फ्यूज अधिकतम $1 W$ सहन कर सकता है, इसका प्रतिरोध ज्ञात करो।View Solution
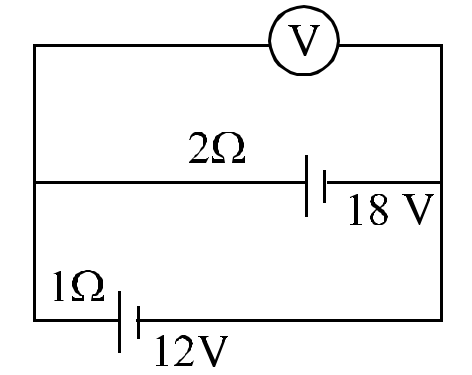
- 36दो बैटरी जिनका वि.बा.ब. $18 V$ तथा $12 V$ तथा आंतरिक प्रतिरोध $2 \Omega$ और $1 \Omega$ है। चित्र में वोल्टमीटर का पाठ्यांक ज्ञात करो।View Solution
- 37लोहे के तार का प्रतिरोध $R$ है। अगर इसकी लम्बाई तथा त्रिज्या दोनों दोगुनी कर दी जाए तो :View Solution
- 38एक बैटरी में $10 \ A$ की धारा 8 घंटे तक प्रवाहित की गयी तो उसका विभव $15 V$ है। यह बैटरी विआवेशित होने पर $15$ घंटे के लिए $5\ A$ की धारा देती है यानि विआवेशीकरण के दौरान इसकी छोर वोल्टता $14$ वोल्ट है। बैटरी की वाट $-$ घंटा क्षमता है:View Solution
- 39तीन एक समान बल्ब $60 W -200 V$ को श्रेणी क्रम में $200 V$ सप्लाई के साथ जोड़ा गया है। इसके द्वारा खर्च शक्ति है-View Solution
- 40एक $6$ वोल्ट की बैटरी को $3 m$ लम्बे तार, जिसका प्रतिरोध $100 \Omega$ है, के साथ जोड़ दिया गया। तार के दो बिन्दुओं जो $500$ सेमी दूरी पर हो विभवांतर के बीच ज्ञात करो।View Solution
- 41$n$ समान प्रतिरोध जिनका मान $r$ है, यदि समान्तर क्रम में जोड़ दिये जाएं तो तुल्य प्रतिरोध होगा :View Solution
- 42भारत में बिजली सप्लाई $220 V$ पर होती है तथा $\text{USA}$ में $110 V$ पर होती है। एक $60 W$ के बल्ब का प्रतिरोध भारत में $R$ है तो $\text{USA}$ में इसका प्रतिरोध में बताइये:$-$View Solution
- 435 प्रतिरोध जिनका मान $R$ है चित्र के अनुसार जोड़े गये है। एक बैटरी $V$ वौल्ट की $A$ तथा $B$ के बीच जोड़ी गयी है। A F C E B में धारा का मान ज्ञात करो:View Solution
- 44View Solutionफ्यूज तार के लिए चाहिए :
- 45एक व्हीटस्टोन ब्रिज की चारों भुजाओं का प्रतिरोध $R$ है। गेल्वेनोमीटर भुजा का प्रतिरोध $R$ है तो तुल्य प्रतिरोध ज्ञात करें।View Solution
- 46View Solutionएक इलैक्ट्रिक केतली में दो कुंडली है। एक कुंडली काम करे तो पानी उबलने में 10 मिनट तथा दूसरी कुंडली काम करे तो पानी उबलने में 40 मिनट लगते है। अगर दोनों कुंडली समांतर क्रम में जोड़े तो पानी उबलने में लगा समय है:
- 47दो बल्ब $220 V -100 W$ के पहले श्रेणी क्रम तथा फिर समांतर क्रम में जोड़े गये। स्रोत $220 V$ a.c. है तो शक्ति खर्च दोनों केस में :View Solution
- 48एक सेल के टर्मिनलों के बीच विभव $2.2 V$ है जबकि सेल खुले परिपथ में है। अगर $5 \Omega$ का प्रतिरोध सेल के टर्मिनलों के बीच लगा दें तो विभव $1.8 V$ हो जाता है। सेल का आन्तरिक प्रतिरोध होगा :View Solution
- 49View Solutionतांबे के तार का विशिष्ट प्रतिरोध :
- 50$Si$ तथा $Cu$ को $300 K$ तक ठण्डा किया गया तो विशिष्ट प्रतिरोधView Solution
- 51एक विभवमापी के तार का विशिष्ट प्रतिरोध $10^{-7} \Omega m$ तथा धारा $0.1 A$ है। इसका पृष्ठ क्षेत्रफल $10^{-6} m ^2$ है तो विभव प्रवणता होगी :View Solution
- 52दो बल्ब $25 W -220 V , 100 W -220 V$ श्रेणी क्रम में $440 V$ के साथ जोड़े गये तो $-$View Solution
- 53एक तार का प्रतिरोध $30^{\circ} C$ पर $3.1 \Omega$ तथा $100^{\circ} C$ पर $4.5 \Omega$ है। तापीय गुणांक :View Solution
- 54एक बैटरी $10 V , 0.5 \Omega$ आंतरिक प्रतिरोध की बाह्य प्रतिरोध $R$ से जोड़ी गयी। $R$ के किस मान के लिए शक्ति उच्चतम है?View Solution
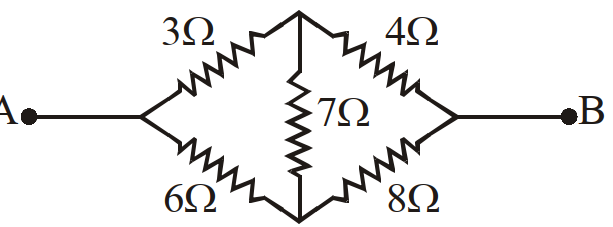
- 55दिये गये परिपथ में $5$ प्रतिरोध जोड़े गये हैं। $A$ तथा $B$ के बीच तुल्य प्रतिरोध ज्ञात करें।View Solution
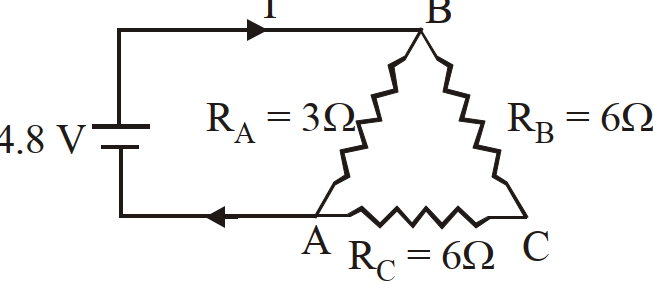
- 56एक कार की बैटरी का वि.वा.ब. $12 V$ तथा आन्तरिक प्रतिरोध $5 \times 10^{-2} \Omega$ है। यह $60 A$ की धारा बनाता है। टर्मिनल वोल्टेज ज्ञात करो।View Solution
- 57दो बल्ब $200 V -40 W , 200 V -100 W,$ घरेलू परिपथ में जुड़े हैं, तोView Solution
- 58View Solutionविद्युत अपघटन में किसी पदार्थ का द्रव्यमान जो उतरा या चढ़ा हो वो समानुपाती है:
- 59View Solutionविभवमापी विभव ज्यादा सही मापता है क्योंकि :
- 60एक मीटर-सेतु की संतुलन लम्बाई 20 सेमी है जबकि दायें गैप में $1 \Omega$ का प्रतिरोध लगाया गया है। बायें गैप में लगाये गये प्रतिरोध का मान ज्ञात करें?View Solution
- 61View Solutionदिये गये परिपथ में धारा का मान :
- 62तीन समान प्रतिरोध एक वि.वा.ब. के स्रोत से जोड़ने पर $10 W$ शक्ति खर्च करते हैं। अगर ये तीनों प्रतिरोध समांतर क्रम में जोड़े तो शक्ति खर्च होगा:View Solution
- 63$10^5 C$ आवेश $1$ ग्राम$-$तुल्यांक एल्यूमिनियम देता है। तो कितनी एल्यूमिनियम $($तुल्यांकी ग्राम $-9)$ मिलेगी जब $I _0$ धारा $20$ मिनट के लिए प्रवाहित की गयी हो?View Solution
- 64View Solutionएक डिसचार्ज नलिका का प्रतिरोध है :
- 65एक चालक में धारा प्रवाहित करने पर ताप में $5^{\circ} C$ की बढ़ोत्तरी होती है। यदि धारा का मान दोगुना कर दें तो तापमान में वृद्धि होगी:View Solution
- 66View Solutionपरिपथ में धारा का मान है:
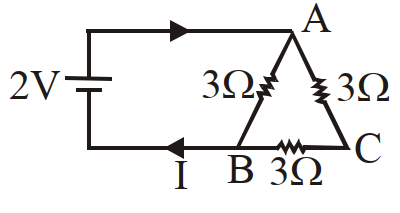
- 67तीन तांबे के तार की लम्बाई तथा पृष्ठ क्षेत्रफल $( L , A ),\left(2 L , \frac{1}{2} A \right),\left(\frac{1}{2} L , 2 A \right)$ है। किसका प्रतिरोध सबसे कम होगा?View Solution
- 68किरचॉंफ का प्रथम नियम $\sum i =0$, किस नियम के संरक्षण पर आधारित है :View Solution
- 69एक बल्ब $(100 W , 200 V )$ को $160 V$ की शक्ति आपूर्ति से जोड़ी गयी। बताओ कितनी शक्ति लगेगी?View Solution
- 70दिये गये परिपथ में बिन्दु $A$ तथा $D$ के बीच तुल्य प्रतिरोध ज्ञात करें।View Solution
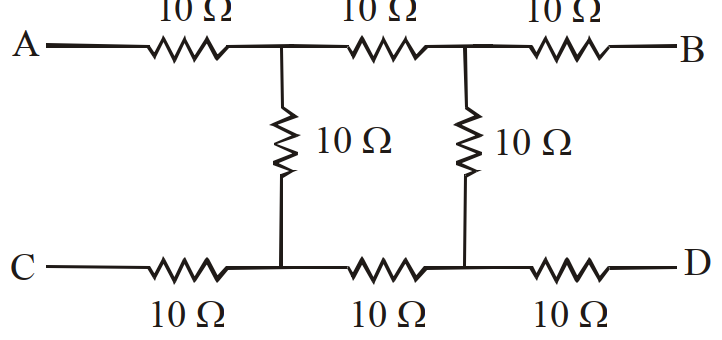
- 71एक तार की लम्बाई $A$ तथा प्रतिरोध $5 \Omega$ है। इसका पृष्ठ क्षेत्रफल $6 \times 10^{-7} m ^2$ है तो इसका विशिष्ट प्रतिरोध ज्ञात करो।View Solution
- 72एक तार का प्रतिरोध $50^{\circ} C$ पर $5 \Omega$ है तथा $100^{\circ} C$ पर $7 \Omega$ है। तार के पदार्थ का औसत तापीय गुणांक क्या होगा?View Solution
- 73दो तार समान लम्बाई के है परन्तु पृष्ठ क्षेत्रफलों का अनुपात $3: 1$ है। इन्हें श्रेणी क्रम में जोड़ा गया। मोटे तार का प्रतिरोध $10 \Omega$ है। इसका तुल्य प्रतिरोध है :View Solution
- 74एक तार जिसका प्रतिरोध $R$ है को पिघलाकर पहले की आधी लम्बाई का नया तार बनाया गया। नये तार का प्रतिरोध होगा :View Solution
- 75$4 \mu F$ का एक संधारित्र $400 V$ पर चार्ज किया गया तथा उसके प्लेटों को $1 k \Omega$ के प्रतिरोध से जोड़ा गया। प्रतिरोध में उत्पन्न ऊष्मा का मान :View Solution
- 76दिये गये चित्र में $4 \Omega$ के प्रतिरोध में प्रवाहित धारा का मान $1.2 A$ है। $B$ तथा $C$ के विभवांतर होगा :View Solution
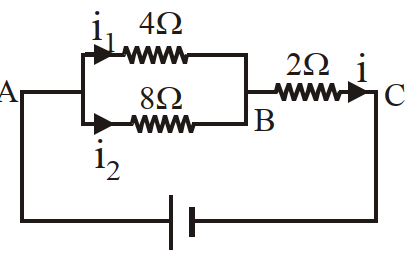
- 77दिये गये चित्र में $3 \Omega$ के प्रतिरोध में $0.8 A$ धार प्रवाहित होती है। ज्ञात करो कि $4 \Omega$ के प्रतिरोध विभवान्तर का मान क्या होगा?View Solution
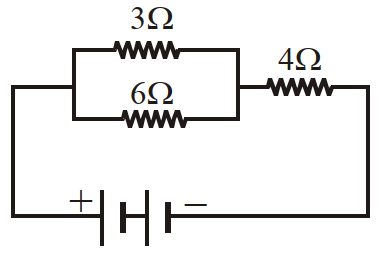
- 78तीन प्रतिरोध $R=4 \Omega$ जुड़कर एक त्रिभुज बनाते हैं किन्हीं दो बिन्दुओं के बीच प्रतिरोध होगा :View Solution
- 79$CuSO _4$ विलयन में दिष्ट धारा प्रवाहित की गयी। इस दो प्लैटिनम के इलेक्ट्रॉंड लगाये गये हैं। जो तत्व इलेक्ट्रों पर एकत्र होंगे वे है:View Solution
- 80View Solutionफैराडे नियम निम्न में से किस के संरक्षण पर आधारित हैं?
- 81View Solutionकिसी धातु में आवेश वाहकों का वेग, सामान्य परिस्थितियों में होगा :
- 82हमारे पास $R=10 \Omega$ के कुछ प्रतिरोध हैं जो कि उच्चतम धारा $1 A$ सहन कर सकते है। हमें इन्हें जोड़कर $5 \Omega$ का तुल्य प्रतिरोध बनाना है जो कि $4 A$ की धारा सहन कर सके। बताइये इस कार्य के लिए कितने कम से कम प्रतिरोधों की आवश्यकता होगी।View Solution
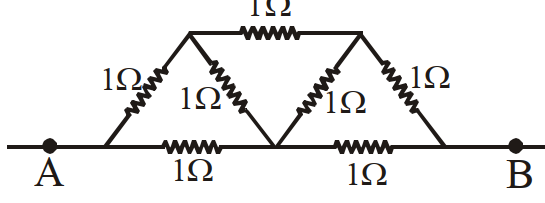
- 83दिये गये चित्र में सभी प्रतिरोध $1 \Omega$ के हैं। $A$ तथा $B$ के बीच तुल्य प्रतिरोध बताइये।View Solution
- 8440 विद्युत बल्ब $220 V$ सप्लाई के साथ श्रेणी क्रम में जोड़े गये। कुछ समय बाद 1 बल्ब खराब हो गया तथा बचे हुए 39 बल्ब फिर समान सप्लाई के साथ श्रेणी क्रम में जोड़े गये। तीव्रता होगी :View Solution
- 85$2 A$ धारा एक तार में प्रवाहित होती है तो $80 J$ ऊष्मा 10 सेकंड में उत्पन्न है। चालक तार का प्रतिरोध (ओम में) है:View Solution
- 86$n$ एक समान प्रतिरोध पहले श्रेणी क्रम में जोड़ें गये तथा फिर समांतर क्रम में जोड़े गये। इसके सर्वाधिक तथा निम्नतम प्रतिरोधों का अनुपात क्या होगा ?View Solution
- 87तांबे के तीन तारों के द्रव्यमान का अनुपात $1: 3$ : 5 तथा इनकी लम्बाई का अनुपात $5: 3: 1$ हैं। इन तारों के विद्युत प्रतिरोध का अनुपात होगा :View Solution
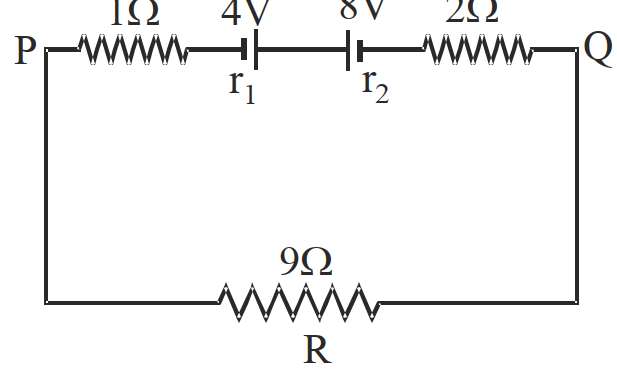
- 88दो सैल जिनके वि.वा.ब. $4 V$ तथा $8 V$ एवं आंतरिक प्रतिरोध $1 \Omega$ तथा $2 \Omega$ है एक $9 \Omega$ के बाहय प्रतिरोध से जुड़े है जैसा कि चित्र में दिखाया गया है। बिन्दु $P$ तथा $Q$ के बीच विभवान्तर तथा धारा का मान होगा:View Solution
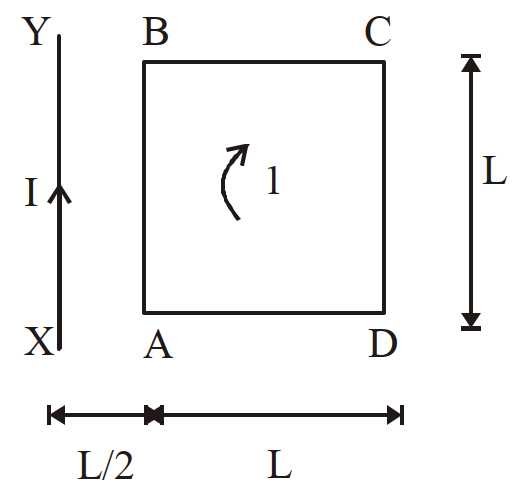
- 89कोई वर्गाकार पाश (लूप) $\text{ABCD}$ जिससे धारा $i$ प्रवाहित हो रही है, किसी लम्बे सीधे चालक $XY$ जिससे धारा I प्रवाहित हो रही है के निकट एक ही तल में रखा है। इस पाश पर लगने वाला नेट बल होगा:View Solution
- 90त्रिज्या $a$ के किसी लम्बे सीधे तार से कोई स्थायी धारा प्रवाहित हो रही है। इस तार की अनुप्रस्थ काट पर धारा एकसमान रूप से वितरित है। तार के अक्ष से त्रिज्य दूरियों $\frac{ a }{2}, 2 a$ पर क्रमशः चुम्बकीय क्षेत्रों $B$ और $B ^{\prime}$ का अनुपात है।View Solution
- 91एक प्रोटॉन तथा एक एल्फा कण, किसी एक समान चुम्बकीय क्षेत्र $B$ के प्रदेश में प्रवेश करते हैं। इनकी गति की दिशा क्षेत्र $B$ के लम्बवत् है। यदि दोनों कणों के लिए वृत्ताकार कक्षाओं की त्रिज्या आपस में बराबर है और प्रोटॉन द्वारा अर्जित की गई गतिज ऊर्जा $1 MeV$ है तो एल्फा कण द्वारा अर्जित ऊर्जा होगीView Solution
- 92एक $0.12 m$ लम्बी, $0.1 m$ चौड़ी कुंडली में तार के $50$ फेरे है इसको $0.2\ \text{weber / m} ^2$ के एकसमान चुम्बकीय क्षेत्र में ऊर्ध्वाधर लटकाया गया है। कुंडली में $2 A$ विद्नुत धारा प्रवाहित हो रही है। यदि कुंडली, चुम्बकीय क्षेत्र से $30^{\circ}$ कोण बनाती है, तो इन्हें रोके रखने के लिए आवश्यक बल आघूर्ण का मान होगा:View Solution
- 93दो सर्वसम $($एक से$)$ लम्बे चालक तार $AOB$ तथा $\operatorname{COD}$ एक-दूसरे के ऊपर, आपस में लम्बवत् रखे गये हैं, और $O$ बिन्दु पर एक दूसरे को काटते हैं तथा इनसे $Øe' Ю$न तथा $I _2$ धारा प्रवाहित हो रही है। बिन्दु $O$ से $d$ दूरी पर, दोनों तारों के तल के लम्बवत् दिशा के अनुदिश किसी बिन्दु $P$ पर चुम्बकीय क्षेत्र का मान होगाView Solution
- 94किसी एमीटर में मुख्य धारा का $0.2 \%$ भाग गैल्वेनोमीटर कुंडली से गुजरता है। यदि गैल्वेनोमीटर की कुंडली का प्रतिरोध $G$ है, तो इस एमीटर का प्रतिरोध होगाView Solution
- 95View Solutionकिसी चुम्बकीय क्षेत्र में एक धारा-पाश (लूप) :
- 96जब किसी कमरे में एक प्रोटॉन को विराम अवस्था से मुक्त किया जाता है तो, यह प्रारंभिक त्वरण $a _0$ से पश्चिम दिशा की ओर गति करता है। यदि इसे $v _0$ वेग से उत्तर दिशा की आरे प्रेक्षित किया जाता है तो यह प्रारंभिक त्वरण $3 a _0$ से पश्चिम दिशा की ओर चलता है तो, इस कमरे में विद्युत तथा चुम्बकीय क्षेत्र हैं:View Solution
- 97किसी प्रोटॉन की गतिज ऊर्जा $1 MeV$ है। यह किसी एक समान चुम्बकीय क्षेत्र में $R$ त्रिज्या के वृत्ताकार पथ में गति कर रहा है तो, किसी $\alpha$-कण की ऊर्जा कितनी होनी चाहिये ताकि वह उसी क्षेत्र में उसी त्रिज्या के पथ में गति कर सके?View Solution
- 98दो एक-जैसी कुंडलीयों की त्रिज्या $R$ है। इनको संकेन्द्रीय इस प्रकार रखा गया है कि उनके समतल, एक दूसरे के लम्बवत् हैं। उनसे प्रवाहित विद्युत धारायें क्रमशः I तथा $2 I$ हैं तो, केन्द्र पर परिणामी चुम्बकीय क्षेत्र प्रेरण होगा:View Solution
- 99एक साइक्लोट्रान का उपयोग प्रोट्रोनों $($द्रव्यमान $=m )$ को त्वरित करने के लिये किया जा रहा है। इसके डीज $($त्रिज्या $R )$ पर $v$ आवृत्ति का एक प्रत्यावर्ती विद्युत क्षेत्र लगाया जाता है तो, साइक्लोट्रॉन में प्रयुक्त प्रचालन चुम्बकीय क्षेत्र $(B)$ तथा उत्पन्न प्रोटॉन किरणपुंज की गतिज ऊर्जा $(K)$ होगी :View Solution
- 100एक मिली वोल्टमीटर का परास $25$ मिली वोल्ट है, इसे $25 A$ परास के एमीटर में रूपान्तरित करना है। इसके लिये आवश्यक शन्ट का मान $($ओम में $)$ होगा :View Solution