Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1एक चुम्बक जिसका चुम्बकीय आघूर्ण $M$ को $90^{\circ}$ से घुमाने में किया गया, $60^{\circ}$ घुमाने में किये कार्य से $n$ गुना ज्यादा है तो $n$ का मान:View Solution
- 2एक छड़ चुम्बक पृथ्वी के चुम्बकीय क्षेत्र में आवर्तकाल $T$ से दोलन करती है। यदि चुम्बक का द्रव्यमान $1 / 4$ कर दे तो आवर्तकाल:View Solution
- 3किसी लम्बी परिनालिका में फेरों की संख्या $1000$ है। जब परिनालिका से $4 A$ धारा प्रवाहित होती है, तब इस परिनालिका के प्रत्येक फेरे से संबद्ध चुम्बकीय फ्लक्स $4 \times 10^{-3} Wb$ है । इस परिनालिका का स्व$-$प्रेरकत्व है:View Solution
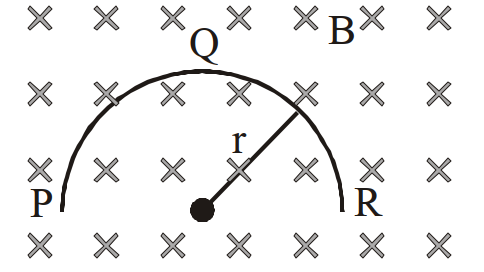
- 4एक इलेक्ट्रॉन सरल रेखीय पथ, $XY$ पर गतिमान है। एक कुंडली abcd इस इलेक्ट्रॉन के मार्ग के निकटवर्ती है (आरेख देखिये) तो, इस कुंडली में प्रेरित धारा (यदि कोई हो तो) की दिशा क्या होगी?View Solution
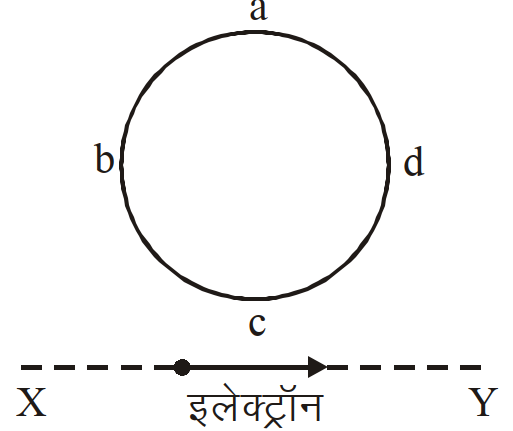
- 5$r$ त्रिज्या की एक पतली अर्द्धवृत्ताकार चालक रिंग (वलय) $( PQR )$ किसी क्षैतिज चुम्बकीय क्षेत्र $B$ में गिर रही है। गिरते समय इसका समतल, आरेख में दर्शाये गये अनुसार, ऊध्र्वाधर रहता है। जब गिरती हुई रिंग की चाल $v$ है तो, इसके दो सिरों के बीच विकसित विभवान्तर होगाView Solution
- 6View Solutionतार का एक पाश (लूप) किसी चुम्बकीय क्षेत्र में घूर्णन करता है तो एक परिक्रमण (चक्र) में इसमें प्रेरित ई.एम. एफ. (e.m.f.) की दिशा में परिवर्तन की आवृत्ति होती है:
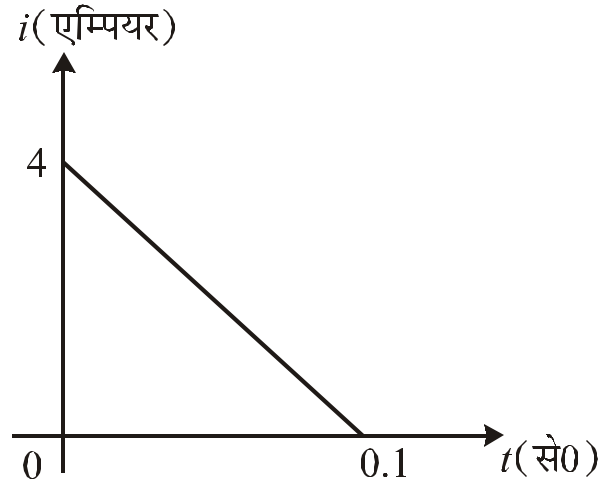
- 7$10 \Omega$ प्रतिरोध की एक कुंडली में, इससे संबद्व चुम्बकीय फ्लक्स के परिवर्तन से प्रेरित विधुत धारा को समय के फलन के रूप में दिये गए आरेख द्वारा प्रदर्शित किया गया है तो, इस कुंडली से संबद्व फ्लक्स में परिवर्तन का मान वेबर में है:View Solution
- 8$400 \Omega$ प्रतिरोध की एक कुंडली को एक चुम्बीय क्षेत्र में रखा गया है। यदि कुंडली से संबद्ध चुम्बकीय फ्लक्स $\phi( wb )$ समय $t$ ( सेकंड) के साथ निम्न प्रकार परिवर्तित होता है, $\phi=50 t ^2+4$ तो कुण्डली में प्रवाहित धारा ( जब $t=2$ सेकंड) होगी:View Solution
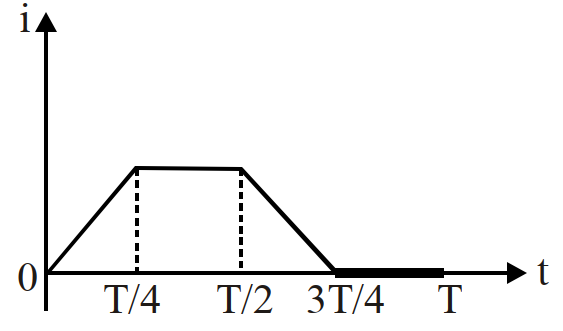
- 9किसी कुण्डली में विद्युतधारा $i$ का मान आरेखानुसार समय के साथ परिवर्तित होता है, तो प्रेरित विद्युत वाहक बल का मान समय के साथ परिवर्तित होगा:View Solution
- 10एक चालक वृताकार पाश ( लूप) को किसी एकसमान चुम्बकीय क्षेत्र में रखा गया है। चुम्बकीय क्षेत्र की तीव्रता $B=.025 T$ है और इसका तल पाश के लम्बवत् है। पाश की त्रिज्या को $1 mm s ^{-1}$ की स्थिर दर से सिकुड़ने दिया जाता है। पाश की त्रिज्या 2 सेमी होने पर उसमें प्रेरिज विद्युत वाहक बल (e.m.f.) हैView Solution
- 11एक आयताकार, एक वर्गाकार, एक वृत्तीय और एक दीर्घवृत्तीय फन्द जो सभी $x - y$ तल में हैं, एक अचर चुम्बकीय क्षेत्र से स्थिर वेग $\overrightarrow{ V }= v \hat{ i }$ से बाहर निकल रहे हैं। चुम्बकीय क्षेत्र की दिशा ऋणात्मक $z$ अक्ष की दिशा में है। क्षेत्र से बाहर निकलने के प्रक्रम में इन फन्दों में प्रेरित वि.वा.ब (emf) स्थिरमानी नहीं रहेगा :-View Solution
- 12एक चालक वृत्तीय फंद को $0.04 T$ के अचर चुम्बकीय क्षेत्र में इस तरह रखा है कि फंद का तल चुम्बकीय क्षेत्र की दिशा से लम्ब दिशा में है। फन्द् की त्रिज्या $2 mm / s$. की दर से घटने लगती है। जब फन्द की त्रिज्या $2 cm$ होगी तो इसमें प्रेरित वि.वा.ब. $( emf )$ का मान होगा:-View Solution
- 13एक लम्बे बहुकुंडलक(सोलिनाइड) में 500 फेरें हैं। जब इसमें 2 ऐम्पीयर की धारा प्रवाहित की जाती है, तो हर फेरे से सम्बन्धित चुम्बकीय फ्लक्स $4 \times 10^{-3} Wb$ होती है। सोलिनाइड का स्वप्रेरकत्व होगा:View Solution
- 14दो कुण्डलियों के स्वप्रेरण $2 mH$ तथा $8 mH$ हैं। दोनों को इतना नजदीक रखा गया कि पहली कुण्डली का चुम्बकीय फ्लक्स दूसरी से भी लिंक हो सके। तो इनके बीच अन्तः प्रेरण है :View Solution
- 15दिये गये चित्र में यदि चुम्बकीय फ्लक्स परिवर्तन कराया जाए $V$ वोल्ट का वि.वा. बल बनता है। एक आवेश $Q$ को लूप पर घुमाने में किया गया कार्य है :View Solution
- 16एक परिपथ जिसका प्रतिरोध $R$ है उसमें लगने वाला चुम्बकीय फ्लक्स $\Delta \phi, \Delta t$ समय में बदल जाता है तो परिपथ में बनने वाला कुल आवेश $Q , \Delta t$ समय में है:View Solution
- 17एक स्वप्रेरण $L =2 mH$ में धारा $i = t ^2 e ^{- t }$ से परिवर्तित होता है। किस समय वि.वा.ब. का मान शून्य होगा:View Solution
- 18दो कुण्डलियों का अन्तः प्रेरण $0.005 H$ है। पहली कुण्डली में धारा $I = I _0 \sin \omega t$ से परिवर्तित होती है जहां $I _0=10 A$ तथा $\omega=100 \pi$ रेडियन/सेकंड तो उच्चतम वि. वा.ब. :View Solution
- 19एक $0.4$ मी लम्बाई वाला चालक $7$ मी/सेकण्ड से चुम्बकीय क्षेत्र $B =0.9$ वेबर $/$ मी $^2$ के लम्बवत् घूमता है। इसमें प्रेरक वि.वा.ब. होगा :View Solution
- 20एक कुण्डली में धारा का मान $10 A$ से $0,5$ सेकण्ड में बदलता है। इसमें औसत प्रेरक वि.वा.ब $220 V$ है। स्व-प्रेणण गुणांक होगा :View Solution
- 21एक कुण्डली का स्वप्रेरण गुणांक होगा, जिसमें $5 V$ का वि.बा.व. बनता हो जबकि धारा $3 A$ से $2 A , 1$ मिली सेकण्ड में परिवर्तित होती होView Solution
- 22एक कुण्डली में फरों की संख्या $N$ है तो स्व-प्रेरण गुणांक किसके समानुपाती होगा?View Solution
- 23View Solutionएक चालक लूप में बनने वाला आवेश, जबकि वह चुम्बकीय क्षेत्र में हो, निर्भर करेगा
- 24एक आयताकार कुण्डली का क्षेत्रफल 25 सेमी $^2$, प्रतिरोध $100 \Omega$ तथा फेरों की संख्या 20 है। यदि चुम्बकीय क्षेत्र कागज के तल के लम्बवत् हो तथा 1000 टेसला/सेकण्ड की दर से बदलता हो तो धारा का मान हैView Solution
- 25एक $100 mH$ कुण्डली में $1 A$ धारा प्रवाहित होती है तो संचित ऊर्जा का मान हैView Solution
- 26View Solutionयदि किसी परिनालिका में प्रति एकांक लम्बाई में फेरों की संख्या दोगुनी कर दी जाए तो उसका स्व-प्रेरण गुणांक होगा
- 27एक कुण्डली जिसमें 50 फेरे हैं एक चुम्बकीय क्षेत्र $2 \times$ $10^{-2} T$ के लम्बवत् रखी जाती है। कुण्डली का क्षेत्रफल 100 सेमी $^2$ है। इसमे उत्पन्न प्रेरक वि.वा.ब. $0.1 V$ है। कुण्डली को 1 सेकण्ड में चुम्बकीय क्षेत्र से हटा दिया जाता है तो $t$ का मान हैView Solution
- 28एक स्वप्रेरक, $L =40 mH$ में धारा $1 A$ से $11 A$ तक $4 ms$ में बढ़ती है। प्रेरक का वि.बा.ब. ज्ञात करें।View Solution
- 29View Solutionएक प्रेरक (inductor) में ऊर्जा संचित होती है-
- 30कोई लघु सिग्नल वोल्टता $V ( t )= V _0 \sin \omega t$ किसी आदर्श संधारित्र $C$ के सिरों पर अनुप्रयुक्त की गयी है:View Solution
- 31किसी स्त्रोत जिसका emf, $V=10 \sin 340 t$ है, से श्रेणी में $20 mH$ का प्रेरक, $50 \mu F$ का संधारित्र तथा $40 \Omega$ का प्रतिरोधक संयोजित है। इस प्रत्यावर्ती धारा परिपथ में शक्ति क्षय है:View Solution
- 32एक श्रेणी $R-C$ परिपथ किसी प्रत्यावर्ती वोल्टता के स्त्रोत से जुड़ा है। दो स्तिथियों $(a)$ तथा $(b)$ पर विचार कीजिए $(a)$ जब संधारित्र वायु भरा है। $(b)$ जब, संधारित्र माइका भरा है। इस परिपथ में प्रतिरोधक से प्रवाहित विद्युत धारा $i$ है तथा संधारित्र के सिरों के बीच विभवान्तर $V$ है तोView Solution
- 33एक ट्रांसफॉर्मर की दक्षता $90 \%$ है तथा यह $200 V$ व $3$ किलोवाट की पावर सप्लाई पर काम कर रहा है। यदि द्वितीयक कुण्डली से $6$ ऐम्पियर की धारा प्रवाहित हो रही है तो, द्वितीयक कुण्डली के सिरों के बीच विभवान्तर तथा प्राथमिक कुण्डली में विद्युत धारा का मान क्रमशः होगाView Solution
- 34एक कुंडली का स्व-प्रेरकत्व $L$ है। यह श्रेणी क्रम मे एक विद्युतबल्ब $B$ तथा एक ए.सी. (A.C.) स्रोत से जुड़ी है। इस बल्ब के प्रकाश की दीप्ति (तीव्रता) कम हो जायेगी, जबView Solution
- 35किसी परिपथ में प्रत्यावर्ती विद्युत धारा तथा वोल्टता के तात्क्षणिक मानों को क्रमशं: निम्न प्रकार निरुपित किया जाता है:View Solution
$ i=\frac{1}{\sqrt{2}} \sin (100 \pi t) \text { एम्पियर } $
तथा $e=\frac{1}{\sqrt{2}} \sin (100 \pi t+\pi / 3)$ वोल्ट तो, इस परिपथ में क्षयित औसत शक्ति वॉट में होगी। - 36किसी प्रेरक में विद्युत धारा (I) समय $t$ के साथ आरेख में दर्शाये गये वक्र के अनुसार परिवर्तित होती हैView Solution
तो, निम्नांकित में से कौन सा ग्राफ (आरेख) समय के साथ वोल्टता के सही परिवर्तन को दर्शाता है?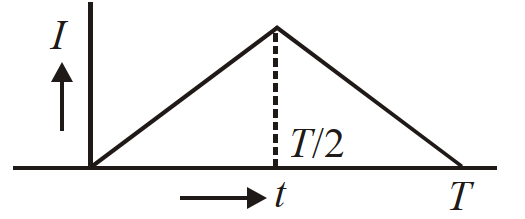
- 37एक विद्युत परिपथ में $R, L, C$ तथा एक ए. सी. वोल्टता स्त्रोत सभी श्रेणी क्रम में जुड़े हैं। परिपथ में से $L$ को हटा देने से वोल्टता तथा विद्युत धारा के बीच कलान्तर $\pi / 3$ हो जाता है, यदि इसके बजाय $C$ को परिपथ से हटा दिया जाये तो, यह कलान्तर फिर भी $\pi / 3$ रहता है। परिपथ का शक्ति गुणांक है :View Solution
- 38ओरख (चित्र) में दिखाये गये विभवान्तर $V$ का वर्ग माध्य मूल (आर.एम.एस.) मान है:View Solution
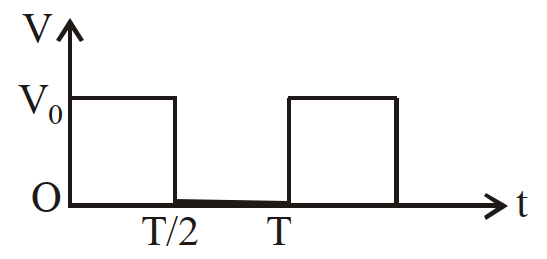
- 39किसी कुण्डली का प्रतिरोध $30$ ओम है तथा $50$ हर्ट्ज आवृत्ति पर प्रेरकीय प्रतिघात $20$ ओम है। यदि कुण्डली के दोनों सिरों के बीच $200$ वोल्ट, $100$ हर्ट्ज का प्रत्यावर्ती धारा का स्रोत जोड़ा जाता है, तो धारा का मान होगा:View Solution
- 40किसी $ac$ परिपथ में एक प्रत्यावर्ती वोल्टता, $e =200 \sqrt{2}$ $\sin 100 t$ वोल्ट, को $1 \mu F$ धारिता के एक संधारित्र से जोड़ा गया है। इस परिपथ में विद्युत धारा का वर्ग-माध्य मूल मान होगा:View Solution
- 41एक $ac$ वोल्टता को श्रेणीक्रम में जुड़े एक प्रतिरोधक $R$ और प्रेरक $L$ पर अनुप्रयुक्त किया गया है। यदि $R$ और प्रेरकीय प्रतिघात में प्रत्येक का मान $3 \Omega$, हो तो, परिपथ में अनुप्रयुक्त वोल्टता और विद्युत धारा के बीच कलान्तर होगा:View Solution
- 42$C$ धारिता के एक संधारित्र को $V_1$ विभवान्तर तक आवेशित किया गया है। फिर इसकी प्लेटों को एक $L$ प्रेरकत्व के एक आदर्श प्रेरक से जोड़ दिया गया है। जब संधारित्र के सिरों के बीच विभवान्तर कम होकर $V_2$ हो जाय तो प्रेरक से बहने वाली धारा होगी?View Solution
- 43दिये गये परिपथ में वोल्टमीट $V_1$ और $V_2$ दोनो के पाठ्यांक $300 V$ हैं, तो वोल्टमीटर $V_3$ और एमीटर $A$ के पाठ्यांक क्रमशः होंगेView Solution
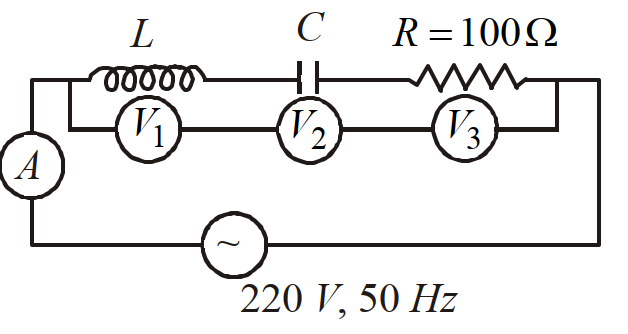
- 44एक ट्रान्सफॉर्मर को $220 V$ का निवेश दिया गया है। निर्गत परिपथ में $440$ वोल्ट पर $2.0 A$ की धारा प्रवाहित होती है। यदि ट्रांन्सफॉमर की दक्षता $80 \%$ हो तो ट्रान्सफार्मर की प्राथमिक कुंडली द्वारा ली गई विद्युतधारा हैView Solution
- 45वि.वा.ब. $( emf ) \varepsilon$ के a.c. स्त्रोत से युक्त श्रृंखला बद्ध LCR परिपथ में ह्रासित शक्ति होती है:-View Solution
- 46एक a.c के क्षणिक वि.वा.ब. (e.m.f.)e और धारा $i$ के क्रमानुसार मान निम्न प्रकार व्यक्त किए जा सकते हैं:View Solution
$e = E _{ o } \sin \omega t$
$i = I _0 \sin (\omega t -\phi)$
a.c. की एक साइकल(आवर्त) में परिपथ में मध्यमान शक्ति होगी : - 47एक ट्रांसफार्मर के प्राथमिक और द्वितीयक कुण्डलियों में फेरों की संख्याएँ क्रमानुसार 50 और 1500 हैं। प्राथमिक कुण्डली से सम्बन्धित चुम्बकीय फ्लक्स $\phi=\phi_0+4 t$, द्वारा व्यक्त होती है जबकि $\phi$ वेबर में है, समय $t$ सेकेण्ड में है और $\phi_0$ एक नियतांक है। द्वितीय कुण्डली से प्राप्त वोल्टता होगी-View Solution
- 48एक श्रेणीबद्ध $\text{LCR}$ परिपथ में $C =10 \mu F$ एवं $\omega=1000$ सेकेण्ड ${ }^{-1}$ हैं। परिपथ में महत्तम धारा के लिये प्रेरकत्व $L$ का मान कितना होना चाहिये?View Solution
- 49$100 W$ और $110 V$ के एक बल्ब को $220 V$ की सप्लाई से प्रदीप्त करने के लिए एक ट्रांसफार्मर का प्रयोग किया गया है। यदि सप्लाई का धारा मान $0.5$ ऐम्पियर हो तो ट्रांसफार्मर की दक्षता होगी, लगभगView Solution
- 50View Solutionएक ट्रांसफार्मर की कुण्डली को लैमिनेट किया जाता है जिससे:
- 51एक परिपथ में $X _{ L }=31 \Omega, R =8 \Omega, X _{ C }=25 \Omega$ श्रेणी क्रम में लगाये गये हैं। इन्हें $110 V$ a.c. के साथ जोड़ा गया है। शक्ति-घटक होगा :View Solution
- 52एक ट्रांसिस्टर दोलनित्र $L - C$ के साथ अनुनाद में है तथा आवृत्ति $f$ है। यदि $L$ को दोगुना व $C$ को चार गुना कर दिया जाए तो आवृत्ति होगी :View Solution
- 53एक $L-C-R$ श्रेणी क्रम परिपथ में आवृत्ति $f$ है। धारा वोल्टेज से $45^{\circ}$ आगे चलती है तो $C$ का मान है :View Solution
- 54$40 H$ की एक कुण्डली के श्रेणी क्रम में $8 \Omega$ प्रतिरोध लगाया गया है। इसके सिरों से $2 V$ की बैटरी जोड़ी गयी तो बताओ समय नियतांक कितना होगा :View Solution
- 55एक श्रेणी क्रम के $L , C , R$ परिपथ में अनुनादीय धारा $i$ है तो शक्ति होगी :View Solution
- 56एक संधारित्र की धारिता $C$ तथा धारितीय प्रतिरोध $X$ है। यदि आवृत्ति तथा धारिता दोगुनी कर दी जाये तो धारितीय प्रतिरोध का मान है:View Solution
- 57एक प्रेरण $L$ तथा प्रतिरोध $R$ को a.c. स्रोत जिसकी कोणीय आवृत्ति $\omega$ हो से जोड़ा गया है। प्रेरण का उच्चता-गुणांक ( $Q$-factor) $Q$ होगा :View Solution
- 58दिये गये परिपथ में प्रेरण $L$ तथा संधारित्र $C$ के साथ $A _1$ तथा $A _2$ दो अमीटर जोड़े गये हैं। यदि कुंजी $K$ दबा दी जाए तो तुरन्त $A _1$ तथा $A _2$ का पाठ्यांक होगा:View Solution
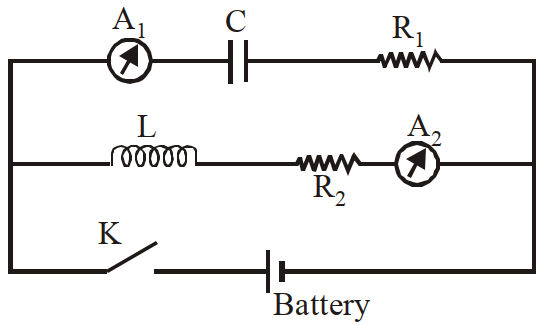
- 59एक स्टेप अप ट्रांसफार्मर $230 V$ पर काम करता है तथा धारा का मान $2 A$ है। प्राथमिक तथा द्वितीयक में फेरों की संख्या का अनुपात $1: 25$ है तो प्राथमिक में धारा का मान हैView Solution
- 60एक A.C. परिपथ में वोल्टेज $V$ तथा धारा I हो तो शक्ति होगीView Solution
- 61एक ट्रांसफार्मर की प्राथमिक कुण्डली में 500 फेरे हैं तथा द्वितीयक कुण्डली में 5000 फेरे हैं। प्राथमिक कुण्डली को $20 V , 50 Hz A . C$. से जोड़ा जाता है। द्वितीयक से कितना निर्गत मिलेगा?View Solution
- 62एक प्रयोग में एक $\text{L-C-R}$ परिपथ को $200 V$ के साथ जोड़ा गया। सर्किट में $X _{ L }=50 \Omega, X _{ C }=50 \Omega$ तथा $R$ $=10 \Omega$ है तो प्रतिबाधा होगीView Solution
- 63एक A.C. परिपथ में $I _{ rms }$ तथा $I _0$ परिबद्ध होंगे:View Solution
- 64View Solutionएक L-C-R श्रेणी परिपथ एक A.C. स्रोत से जुड़े है। अनुनादीय स्थिति में धारा तथा वोल्टेज के बीच कलांतर होगा :
- 65एक $C - R$ परिपथ का समय गुणांक होगाView Solution
- 66View Solutionदिये गये चित्र में बल्ब अचानक चमकता है यदि
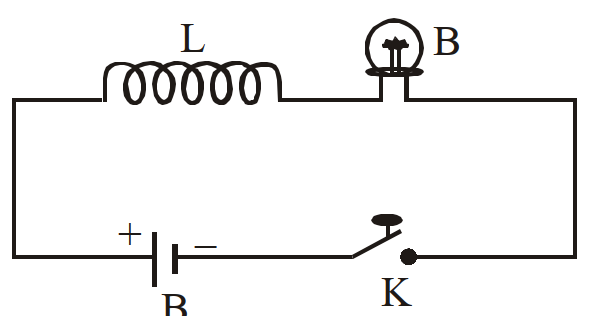
- 67View Solutionएक धारा प्रवाहित कुण्डली में ऊर्जा किस रूप में संचित होती है?
- 68View Solutionभँवर (Eddy) धाराएं बनती हैं जब
- 69एक धारा प्रवाहित कुण्डली जिसकी त्रिज्या 30 सेमी तथा प्रतिरोध $\pi^2 \Omega$ है को एक चुम्बकीय क्षेत्र $B =10^{-2} T$ वाले क्षेत्र में चुम्बकीय क्षेत्र के लम्बवत् घुमाया जातो है। यदि घुमाने की दर $200 rpm$ हो तो उत्पन्न प्रत्यावर्ती धारा का अधिकतम मान होगा:View Solution
- 70View Solutionनीचे दिए गए विकल्पों में से किसका उपयोग एक संचरित विद्युत चुम्बकीय तरंग उत्पत्र करने में किया जा सकता है?
- 71किसी विद्युत चुम्बकीय तरंग की ऊर्जा की कोटि 15 $keV$ है। यह स्पैक्ट्रम के किस भाग का सदस्य है?View Solution
- 72$25 \times 10^4$ वाट/मी ${ }^2$ ऊर्जा फ्लक्स का प्रकाश, किसी पूर्णतः परावर्तक पृष्ठ $($ सतह $)$ पर लम्बवत् आपतित होता है। यदि इस पृष्ठ का क्षेत्रफल 15 सेमी $^2$ हो तो, पृष्ठ पर आरोपित औसत बल होगाView Solution
- 73View Solutionनिम्नलिखित में से किस दशा में किसी माइक्रोवेब (सूक्ष्म तरंग) ऑवन की जल अणु युक्त भोजन पदार्थों को गर्म की दक्षता महत्तम होगी?
- 74View Solutionनिर्वात में संचरित किसी विधुत चुम्बकीय तरंग के लिये चुम्बकीय तथा वैधुत क्षेत्रों के आयामों का अनुपात होता है:
- 75निर्वात में किसी विद्युत चुम्बकीय तरंग से संबद्ध वैद्युत क्षेत्र को $\vec{E}=\hat{i} 40 \cos \left(k z-6 \times 10^8 t\right)$, द्वारा व्यक्त किया जाता है। जहाँ $E, z$ तथा $t$ क्रमशः वोल्ट / मीटर, मीटर तथा सेकण्ड $(s)$ में है तो, तरंग सदिश $(k)$ का मान है :View Solution
- 76View Solutionअवरक्त किरणों, सूक्ष्म तरंगों, पराबैंगनी तरंगों और गामा किरणों की तरंगदैर्ध्य घटते क्रम में है:
- 77$+z$-अक्ष की दिशा में गमन करती हुई विद्युत चुम्बकीय तरंगो से सम्बद्ध विद्युत और चुम्बकीय क्षेत्रों को निरूपित किया जा सकता है:View Solution
- 78मुक्त आकाश में किसी विद्युत चुम्बकीय तरंग का विद्युत क्षेत्रView Solution
$\vec{E}=10 \cos \left(10^7 t+k x\right) \hat{j} V / m$ से निरूपित (प्रकट) किया जाता है। जहाँ $t$ सेकेण्ड में और $x$ मीटर में है।
इससे यह निष्कर्ष निकलता है कि
(1) तरंगदैर्ध्य $\lambda=188.4 m$
(2) तरंग संख्या $k=0.33 rad / m$
(3) तरंग-आयाम $=10 V / m$
(4) तरंग $+x$ दिशा की ओर गमन कर रही है।
निम्नलिखित प्रकथनों के युग्मों में से कौन सा ठीक है? - 79View Solutionविद्युत चुम्बकीय तरंगो के गुणों के लिये कौन सा कथन सत्य (सही) नहीं है?
- 80एक माध्यम में विद्युत चुम्बकीय तरंग का वैद्युत क्षेत्री भाग निम्न प्रकार सूचित है $E _{ x }=0$;View Solution
$ E _{ y }=2.5 \frac{ N }{ C } \cos \left[\left(2 \pi \times 10^6 \frac{ rad }{ m }\right) t -\left(\pi \times 10^{-2} \frac{ rad }{ s }\right) x \right]$
$E _{ z }=0 $,यह तरंग - 81विद्युतशीलता $\epsilon_0$ और चुम्बकशीलता $\mu_0$ के माध्यम में विद्युत-चुम्बकीय विकिरण का वेग होता है:View Solution
- 82View Solutionएक विद्युत-चुम्बकीय तरंग के विद्युत और चुम्बकीय क्षेत्र
- 83View Solutionमाना कि मानव से भी विकिरण उत्सर्जित होता है तो बताओ कौन सा वचन सत्य है :
- 84View Solutionइनमें से कौन विद्युत चुम्बकीय तरंग नहीं है?
- 85यदि $\overrightarrow{ E }$ तथा $\overrightarrow{ B }$ किसी वैद्युत चुम्बकीय तरंग के लिए विद्युत तथा चुम्बकीय क्षेत्र बताती हो तो तरंग के चलने की दिशा होगी :View Solution
- 86View Solutionसबसे कम तरंगदैर्ध्य किसकी होगी?
- 87View Solutionपृथ्वी पर होने वाले ग्रीन हाउस प्रभाव का कारण है:
- 88View Solutionविद्युत चुम्बकीय विकिरण का कारण है-
- 89यदि निर्वात में विद्युतशीलता $\epsilon_0$ तथा चुम्बकीयशीलता $\mu_0$ हो तथा किसी माध्यम में इसका मान $\in$ तथा $\mu$ हो तो माध्यम का अपवर्तनांक होगाView Solution
- 90View Solutionएक वैद्युत चुम्बकीय तरंग के वैद्युत तथा चुम्बकीय क्षेत्र एक दूसरे से होते हैं
- 91View Solutionकिसकी तरंगदैर्ध्य सबसे कम होगी?
- 92View Solutionठोसों की संरचना को देखने हेतु प्रयोग की जाती है :-
- 93एक कण की त्रिज्या $3 \times 10^{-4}$ सेमी है। इसे देखने हेतु उचित वैद्युत चुम्बकीय तरंग की आवृति की कोटि हैView Solution
- 94View Solutionकिसकी तरंगदैर्ध्य सबसे अधिक होगी-
- 95प्रिज्म के किसी अपवर्तक पृप्ठ पर किसी प्रकाश किरण के लिए आपतन कोण का मान $45^{\circ}$ है। प्रिज्म कोण का मान $60^{\circ}$ है। यदि यड किरण प्रिज्म से न्यूनतम विचतित होती है, तो न्यूनतम विचलन कोण तथा प्रिज्म के प्रदार्थ का अपवर्त्तनांक क्रमश: हैःView Solution
- 96किसी खगोलीय दूरबीन के अभिदृश्यक और नेत्रिका की फोक्स दूरियां कमश: $40$ से.मी. और $4$ से.मी. हैं। अभिदृश्यक से $200$ से.मी. दूर स्थित किसी बिम्ब को देखने के लिए दोनों लेंसों के बीच की दूरी होनी चाडिए:View Solution
- 97कॉलम -1 की संगत प्रविप्टियों का मिलान कॉलम 2 प्रविप्टियों से कीजिए। यहाँ ' $m$ ' दर्पणों द्वारा उत्पत्र आवर्धन हैं।View Solution
कॉलम -1 कॉलम -2 (A) $m =-2$ (a) उत्तल दर्पण (B) $m =-\frac{1}{2}$ (b) अवतल दर्पण (C) $m =+2$ (c) वास्तविक प्रतिबिम्ब (D) $m =+\frac{1}{2}$ (d) आभासी प्रतिबिम्ब - 98सामान्य समायोजन की स्थिति में, किसी खगोलीय दूरदर्शक के अभिदश्यक लेंस के भीतरी भाग पर $L$ लम्बार्ई के एक काली सरता रेखा खिची गर्ई है। नेत्रिका इस सरल रेखा का वास्तविक प्रतिबिम्ब बनाती है। प्रतिबिम्ब की लम्बाई $l$ है तो दूरदर्शक का आवर्थन है :View Solution
- 99एक प्रकाश किरणपूंज, लाल, हरे तथा नीले रंगों से बना है। यड किरणपुंज किसी समकोणी प्रिज्म पर आपतित होता है $($ आरेख देखिये $)$ प्रिज्म के पदार्थ का अपवर्तनांक, लाल, हरे, व नीले रंग के लिये क्रमश: $1.39$, $1.44$ तथा $1.47$ है, तो यह प्रिज्म:View Solution
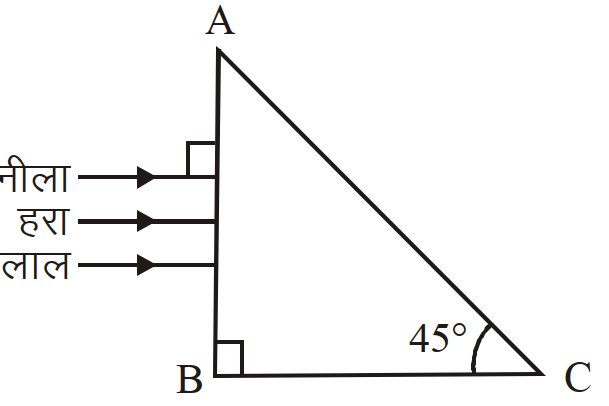
- 100किसी प्रिज्म का कोण $A$ है। इस प्रिन्म के एक अपवर्तक फलक को रजतित कर परावर्तक बना दिया गया है, इसके पृष्ठ पर, $2 A$ कोण पर आपतित प्रकाश की किरणें, रजतित फलक से परावर्तन के पश्चात् अपने मार्ग पर वापस आ जाती हैं। प्रिज्म के पदार्थ का अपवर्तनांक $\mu$ होगाView Solution