Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1View Solutionयदि, अभिदृश्यक लेन्स की फोकस दूरी को बढ़ा दिया जाय, तो
- 2सामान्य नेत्त्र में कौर्निया $($स्वच्छ मंडल$)$ की अभिसारी शक्ति $40 D$ है तथा कार्निया के पीछे नेत्र लेंस की न्यूनतम अभिसारी शक्ति $20 D$ है। इस सूचना से नेत्र के रेटिना $($दृष्टिपटल$)$ तथा लेन्स के बीच की अनुमानित दूरी होगी:View Solution
- 3एक समतल उत्तल और एक समतल अवतल लेंस एक दूसरे के ऊपर पूर्णतः ठीक बैठ जाते हैं। उनके समतल पृष्ठ आपस में समान्तर हैं। यदि इन लेंसों के पदार्थां के अपवर्तनांक $\mu_1$ और $\mu_2$ हैं तथा दोनों के वक्र पृष्ठों $($ तलों $)$ की वक्रता त्रिज्या $R$ है तो इनके संयोजन की फोकस दूरी होगी :View Solution
- 4View Solutionकिसी प्रिज्म के न्यूनतम विचलन कोण का मान उसके अपवर्तक कोण के बराबर होगा यदि प्रिज्म के पदार्थ का अपवर्तनांक हो:
- 5$10 cm$ लम्बी एक छड़ को, $10 cm$ फोकस दूरी के एक अवतल लेंस की मुख्य अक्ष के अनुदिश इस प्रकार रखा गया है कि छड़ का दर्पण के ध्रुव के पास वाला सिरा, दर्पण से $20 cm$ दूर है। प्रतिबिम्ब की लम्बाई होगी :View Solution
- 6एक दूरदर्शी यंत्र का आवर्धन क्षमता $9$ है। जब इसे समान्तर किरणों के लिए समायोजित किया जाता है तब इसके अभिदृश्यक तथा नेत्रिका के बीच की दूरी $20 \ cm$ होती है। इन लेंसों की फोकस दूरियाँ क्रमश होगी:View Solution
- 7जब $1.47$ अपवर्तनांक के कॉंच के किसी उभयोत्तल लैंस को किसी द्रव में डुबाया जाता है तो, यह एक समतल शीट $($ परत $)$ की भॉंति व्यवहार करता है। इसका तात्पर्य यह है कि द्रव का अपवर्तनांक हैःView Solution
- 8प्रकाश की एक किरण, किसी प्रिज्म जिसका कोण $A$ है के एक फलक पर $i$ कोण पर आपत्तित होती है तथा उसके विपरीत फलक से उसके लम्बवत् निर्गत होती है। यदि प्रिज्म का अपवर्तनांक $\mu$ है तो, आपतन कोण $i$ का मान लगभग बराबर है :View Solution
- 9' $f_1$ ' फोकस दूरी का एक अवतल दर्पण, ' $f_2$ ' फोकस दूरी के एक उत्तल लेंस से $d$ दूरी पर रखा गया है। अनन्त से आता हुआ एक किरण पुंज, उत्तल लेंस तथा अवतल दर्पण के इस संयोजन पर टकराता है और अपने मार्ग पर अनन्त को वापस हो जाता है तो, दूरी ' $d$ ' का मान होगा :View Solution
- 10काँच के किसी पतले प्रिज्म का कोण $15^{\circ}$ है और उसका अपवर्तनांक $\mu_1=1.5$ है। इसका $\mu_2=1.75$ अपवर्तनांक के किसी अन्य प्रिज्म से संयुक्त किया गया है। इनसे बने प्रिज्मों के संयोजन से विचलन बिना परिक्षेपण प्राप्त होता है। तो दूसरे प्रिज्म का कोण होना चाहिये:View Solution
- 11प्रकाश का एक अभिसारी किरण पुंज किसी अपसारी लेंस पर आपतित होता है। लेंस से गुजरने के पश्चात, प्रकाश की किरणें लेंस के दूसरी ओर, उससे $15 \ cm$ दूरी पर, एक दूसरे का प्रतिच्छेदन करती है $($ काटती $)$ है। यदि लेंस को हटा दिया जाये तो किरणों का प्रतिच्छेदन बिन्दु, लेंस से $5 \ cm$ और पास (समीप) हो जाता है। तो, लेंस की फोकस दूरी है:View Solution
- 12View Solutionनिम्नलिखित में किसका कारण पूर्ण आन्तरिक परावर्तन नहीं है?
- 13किसी उभयोत्तल लेंस की वक्रता त्रिज्या का परिमाप $20 \ cm$ है। इसके सामने इससे $30 \ cm$ दूर रखी $2 \ cm$ ऊंची वस्तु का प्रतिबिम्ब होगा:View Solution
- 14दो माध्यमों $M_1$ और $M_2$ में प्रकाश की चाल क्रमशः $1.5 \times 10^8 m / s$ और $2.0 \times 10^8 m / s$ है। प्रकाश की एक किरण माध्यम $M_1$ से $M_2$ में $i$ आपतन कोण पर प्रवेश करती है। यदि इस किरण का पूर्ण आतंरिक परावर्तन हो जाता है तो, ' $i$ ' का मान हैView Solution
- 15$60^{\circ}$ के किसी प्रिज्म पर प्रकाश की एक किरण अल्पतम् विचलन की स्थिति पर आपतित होती है। पहले पाश्र्व (फलक) पर (अर्थात् आपतन पाश्र्व पर) अपवर्तन कोण हैView Solution
- 16$f$ फोकस दूरी और $d$ व्यास के द्वारक वाला एक लैंस, तीव्रता $I$ का एक प्रतिबिम्ब बनता है। लेंस के केन्द्रीय भाग में $\frac{d}{2}$ व्यास के द्वारक को काले कागज से ढक दिया जाता है। लेंस की फोकस दूरी तथा प्रतिबिम्ब की तीव्रता अब क्रमशः होगीView Solution
- 17अपवर्तनांक $\mu$ के एक पारदर्शी माध्यम से चलती हुई प्रकाश की एक किरण, इस माध्यम और वायु को पृथक करने वाली सतह पर $45^{\circ}$ के कोण पर टकराती है। अपवर्तनांक $\mu$ के किस मान के लिए इस किरण का पूर्ण आंतरिक परावर्तन हो जायेगा?View Solution
- 18कोई लड़का कागज़ पर एक समउत्तल लैंस द्वारा सूर्य किरणों को फोकस कर आग जलाना चाहता है। लैंस की फोकस दूरी $10 cm$ है। सूर्य का व्यास $1.39 \times 10^9 m$ है और इसकी पृथ्वी से मध्यमान दूरी $1.5 \times 10^{11} m$ है। सूर्य के कागज़ पर प्रतिबिम्ब का व्यास होगा:View Solution
- 19$f _1$ और $f _2$ फोकस दूरियों के दो पतले लैंस अक्षीय रूप से जुड़े हुए हैं। इस युग्म की शक्ति (पावर) होगी :View Solution
- 20एक माध्यम में किसी प्रकाश तरंग की आवृत्ति $2 \times 10^{14} Hz$ है और इसकी तरंगदैर्ध्य $5000 A$ है। माध्यम का अपवर्तनांक होगा-View Solution
- 21View Solutionकिसी द्रव से भरे एक बीकर के तल पर एक लघु सिक्का रखा गया है। चित्र के अनुसार एक प्रकाश किरण सिक्के से आरम्भ होकर द्रव के ऊपरी तल तक पहुँच कर तल के समांतर चलती है।
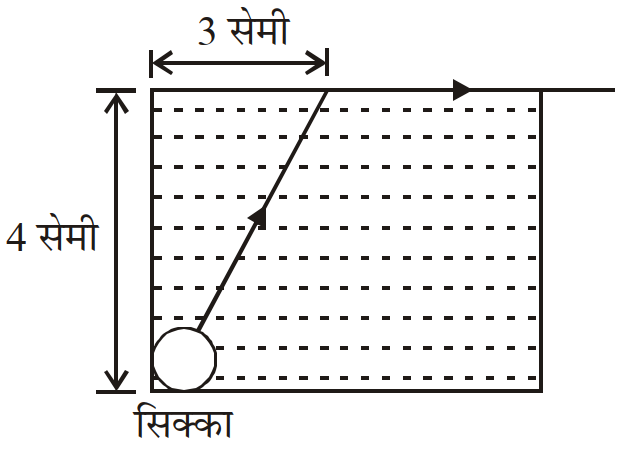
इस द्रव में प्रकाश चलन का वेग कितना होगा? - 22View Solution25 सेमी की समान फोकस दूरी के उत्तल और अवतल लेंसों को जोड़ कर प्राप्त लेंस संयोजन की शक्ति डायोप्टर में होगी:
- 23एक सूक्ष्मदर्शी को कागज पर बने एक निशान पर फोकस करने के उपरान्त इस निशान पर $1.5$ अपवर्तनांक के काँच के 3 सेमी मोटे स्लैब को रखा गया है। अब सूक्ष्मदर्शी में क्या स्थानान्तरण किया जाए कि निशान फिर से फोकस में आ जाए ?View Solution
- 24$5000 A$ तरंगदैर्ध्य पर $10$ सेमी व्यास के अभिदृश्यक युक्त दूरदर्शी के कोणीय विभेदन का क्रम है:View Solution
- 25View Solutionलाल तथा हरी किरणों से बना हुआ एक प्रकाश पुँज आयताकार काँच की पट्टिका के पृष्ठ पर स्थित एक बिन्दु पर त्रिर्यक रूप से आपतित होता है। जब प्रकाश पुँज विपरीत समान्तर पृष्ठ पर आता है, तो लाल तथा हरी किरणें:
- 26प्रिज्म के पदार्थ का अपवर्तनांक $\sqrt{2}$ तथा इसका अपवर्तन कोण $30^{\circ}$ है। प्रिज्म के अपवर्तक पृष्ठों में से किसी एक पृष्ठ को अन्दर की ओर दर्पणनुमा बनाया जाता है। दूसरे पृष्ठ पर आपतित एकवर्णी प्रकाश पुँज दर्पण से परावर्तित होकर अपने ही मार्ग से वापिस लौट आएगा यदि प्रिज्म पर आपतन कोण है:View Solution
- 27एक दूरदर्शी के अभिदृश्यक लेन्स का व्यास 10 सेमी है तथा यह दो वस्तुओं से 1 किमी दूरी पर स्थित है। दूरदर्शी द्वारा विभेदित दोनों वस्तुओं के बीच की न्यूनतम दूरी, जब प्रकाश की माध्य तरंगदैर्ध्य $5000 A$ है, होगी:View Solution
- 28एक द्विउत्तल लैंस को दो भगों में काटा गया है (i) $XOX ^{\prime}$ के अनुदिश (ii) $YOY ^{\prime}$ के अनुदिश, यदि $f , f ^{\prime}$, f" तीनों स्थितियों में लैंस की फोकस दूरियां हैं तो निम्न में से कौन-सा सम्बन्ध सही है:View Solution
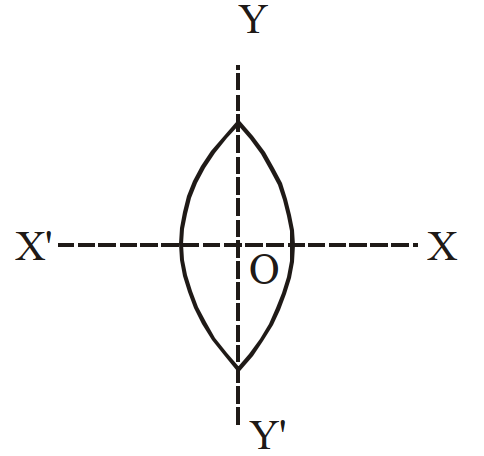
- 29View Solutionएक उत्तल लैंस को ऐसे द्रव में डुबोया जाता है, जिसका अपवर्तनांक लैंस के पदार्थ के अपवर्तनांक के बराबर है तो इसकी फोकस दूरी होगी:
- 30देखने पर दीवार के समान्तर तथा समान साइज का प्रतिबिम्ब दिखायी पड़ता है। दूसरी दीवार से लेंस $d$ दूरी पर रखा हो तो उसकी फोकस दूरी होगी :View Solution
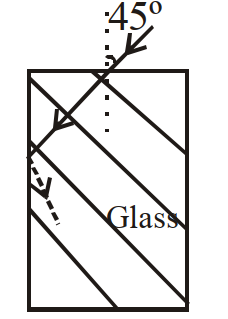
- 31View Solutionएक प्रकाश किरण काँच के गुटके पर चित्रानुसार पड़ती है। यदि उर्ध्वाधर पृष्ठ से पूर्ण आंतरिक परावर्तन हुआ हो तो काँच का अपवर्तनांक होगा :
- 32View Solutionइंद्रधनुष किसके संयोजन से बनता है?
- 33View Solutionएक व्यक्ति 6 फुट लम्बाई का है। इसे अपना पूरा प्रतिबिम्ब देखने के लिए कितने ऊँचे समतल दर्पण की आवश्यकता होगी ?
- 34एक काँच के गुटके में $(\mu=1.5)$ एक हवा का बुलबुला है। इसकी दूरी एक पृष्ठ से 5 सेमी तथा दूसरे से 2 सेमी दिखायी देती है। गुटके की मोटाई बताओ।View Solution
- 35एक पतले समतलोत्तल लैंस की वक्रता त्रिज्या 10 सेमी तथा अपवर्तनांक $1.5$ है। यदि समतल पृष्ठ को पोलिश कर दिया जाए तो यह अवतल दर्पण का काम करेगा। इसकी फोकस दूरी है:View Solution
- 36प्रकाश की तरंग दैर्ध्य क्या होगी जिसकी आवृत्ति $100 Hz$ है?View Solution
- 37प्रिज्म के पदार्थ का अपवर्तनांक $\sqrt{3}$ है। न्यूनतम विचलन कोण का मान होगा :View Solution
- 38एक समतलोत्तल लेंस का अपवर्तनांक $\mu=1.6$ है। इसके वक्र पृष्ठ की वक्रता त्रिज्या $60$ सेमी है। इसकी फोकस दूरी क्या होगी।View Solution
- 39एक पारदर्शी छड़ का अपवर्तनांक $n$ है। इसमें प्रकाश अन्दर जाता है। अपवर्तनांक का मान क्या होगा यदि प्रकाश दूसरे सिरे से बाहर न निकले चाहे आपतन कोण का मान कुछ भी क्यों न हो?View Solution
- 40एक प्रकाशदीप्त वस्तु उत्तल लेंस से $f =20$ सेमी दूरी पर रखी है। लेंस के दूसरी तरफ एक 10 सेमी वक्रता त्रिज्या का उत्तल दर्पण रखा है। बताओ इसकी दूरी लेंस से क्या होगी कि प्रतिबिम्ब वस्तु की जगह पर हीं बनेView Solution
- 41एक उत्तल लेंस की बैंगनी, हरे तथा लाल रंग के लिए फोकस दूरियां $f_V, f_g, f_r$ है तो :View Solution
- 42एक विद्युत चुम्बकीय तरंगों की आवृत्ति, $n$ तथा तरंग दैर्ध्य $\lambda$ है । यह हवा में $v$ वेग से चलता हुआ $\mu$ अपवर्तनांक वाले काँच में जाता है। कांच में इसकी आवृत्ति, तरंगदैधर्य तथा वेग ज्ञात करोView Solution
- 43View Solutionएक खगोलीय दूरदर्शी की ट्यूब की लम्बाई 44 सेमी है तथा आवर्धन 10 है। इसके वस्तु लेंस की फोकस दूरी होगी :
- 44उत्तल लेंस के लिए बैगनी तथा लाल प्रकाश के लिए फोकस दूरियां $f_V$ तथा $f_R$ है। अवतल लेंस के लिए यही फोकस दूरियां $F _{ V }, F _{ R }$ हैं । तोView Solution
- 45प्रकाश एक $t$ मोटाई तथा $\mu$ अपवर्तनांक के कांच से गुजरता है । यदि प्रकाश का वेग $c$ हो तो प्रकाश को काँच से गुजरने में लगा समय होगा :View Solution
- 46एक उत्तल लेंस $f=80$ सेमी तथा अवतल लेंस $f=50 cm$ को जोड़कर रखा गाया है। युग्म की क्षमता होगीःView Solution
- 47एक काँच के ब्लॉक के एक पृष्ठ को पौलिश किया गया है। इसकी मोटाई $6$ सेमी है। एक वस्तु पहले पृष्ठ से $8$ सेमी दूर रखी गयी है, पॉलिश पृष्ठ के $12$ सेमी पीछे इसका प्रतिबिम्ब बनता है । कांच का अपवर्तनांक होगा:View Solution
- 48View Solutionएक अवर्णी युग्म बनेगा
- 49दो समतल दर्पण एक दूसरे से $60^{\circ}$ कोण बनाते हुए रखे गये हैं। एक कण इनके बीच रखा गया है बताओ इसके कितने प्रतिबिम्ब बनेंगे?View Solution
- 50एक लेंस, प्रकाश स्रोत्र तथा दीवार के बीच रखा है। यह लेंस के दो भिन्न स्थितियों दीवार पर $A _1$ तथा $A _2$ क्षेत्रफल के दो प्रतिबिम्ब बनाता है। प्रकाश स्रोत्र का क्षेत्रफल होगाView Solution
- 51View Solutionदूर दृष्टि दोष है
- 52विचलन कोण $\delta$, अपवर्तनांक $\mu$ तथा प्रिज्म कोण $A$ है तो निम्न में से कौन सा कथन सत्य है?View Solution
- 53पानी की सतह के 4 मीटर नीचे एक प्रकाश स्रोत्र रखा जाता है। पानी का अपवर्तनांक $5 / 3$ है। पानी सतह पर जो प्रकाश डिस्क बनेगी उसका व्यास होगा :View Solution
- 54View Solutionउत्तल लैस की फोकस दूरी उच्चतम होगी
- 55सूर्यकिणणें एक कांच की खिड़की से गुजरने में कितना समय लेगी । कांच की मोटाई 4 मिमी तथा अपवर्तनांक $3 / 2$ है।View Solution
- 56एक प्रिज्म का अपवर्तनांक $\sqrt{2}$ तथा आपतन कोण $30^{\circ}$ है। एक समतल को पोलिश कर दिया गया। एक वर्णी प्रकाश तरंग अपने पथ को वापस पार करती है यदि आपतन कोण का मान होगा :View Solution
- 57हरें रंग का प्रकाश $(\lambda=5460 A)$ का हवा-कांच के समतल पर पड़ता है। कांच का अपवर्तनांक $1.5$ है प्रकाश की कांच में तरंग दैर्ध्य होगी ( $c=3 \times 10^8$ मी/सेकंड)View Solution
- 58View Solutionनिम्न विकिरणों में किसकी तरंगद्धर्य अधिकतम है
- 59एक प्रिज्म जिसका कोण $A$ है, के एक समतल पर एक किरण आपतन कोण बनाते हुए आती है तथा वह दूसरे समतल के लम्बवत बाहर निकलती है। यदि प्रिज्म के पदार्थ का अपवर्तनांक $\mu$ हो तो आपतन कोण $i$ का मान लगभग होगा:View Solution
- 60View Solutionकिन विमाओं के लिए किरण प्रकाशिकी लागु होता है?
- 61अपवर्तनांक $1.5$ की एक उत्तल लेंस की फोकस दूरी 2 सेमी है। यदि लेंस को $1.25$ अपवर्तनांक वाले पदार्थ में डुबो दिया जाए तो फोकस दूरी होगी:View Solution
- 62यंग के किसी द्वि द्रिरी प्रयोग में उच्चिप्ठ की तीव्रता $I _0$ है। दोनों द्भिरियों के बीच की दूरी $d =5 \lambda$ है, यहाँ $\lambda$ प्रयोग में उपयोग किए गए प्रकाश की तरंगदैर्घ्य है। किसी एक झिरिी के सामने दूरी $D =10 d$ पर स्थित पर्द पर तीव्रता क्या होगी?View Solution
- 63जब चौड़ार्ई ' $a$ ' की किसी एकल डिरी पर $5000 A$ तरंगदैर्घ्य का प्रकाश आपतन करता है, तो झिरी के कारण उत्पत्र विवर्तन पैटर्न में $30^{\circ}$ के कोण पर पहला निम्निप्ठ दिखाई देता है। पहला द्वितीयक उच्चिप्ठ जिस कोण पर दिखार्ई देगा, वह है:View Solution
- 64एकला डिरी विवर्तन पैटर्न में, केन्द्रीय उच्चिप्ट के निकटवर्ती प्रथम निम्निप्ट पर, डििरी के किनारे तथा उसके मघ्य$-$बिन्दु से उत्पन्न हाइगेन्स-तरंगिकाओं के बीच कलान्तर होता है:View Solution
- 65यंग के किसी द्विडिरी प्रयोग में, दो झिरियों की चौड़ाइयों में अनुपात $1: 25$ है, तो व्यतिकरण पैटर्न में उच्चिप्ट तथा निम्नप्ठ की तीव्रताओं का अनुपात, $\frac{I_{\max }}{I_{\min }}$ होगा:View Solution
- 66दूर स्थित किसी स्रोत से आता हुआ, $\lambda=600$ नैनोमीटर का प्रकाश पुंज, $1$ मिमी चौड़ी झिरी पर आपतित होता है। इससे उत्पन्न विवर्तन पैटर्न को झिरी से $2$ मी दूर स्थित पर्दे पर देखा जाता है तो, केन्द्रीय दीप्त फ्रिन्ज के दोनों ओर की प्रथम अदीप्त फ्रिन्जों के बीच की दूरी होगीView Solution
- 67यंग के द्वि$-$झिरी प्रयोग में, पर्द् के किसी बिन्दु पर $\lambda$ पथान्तर होने से, वहां प्रकाश की तीव्रता $K$ है, $( \lambda$ प्रयुक्त प्रकाश की तरंगदैर्ध्य है$)$। पर्द के उस बिन्दु पर जहां पथान्तर $\lambda / 4$ है, तीव्रता होगीView Solution
- 68View Solutionद्रुत वेग से चलती हुई इलेक्ट्रॉनों की एक समान्तर किरणपुंज, किसी पतली झिरी पर लम्बवत् आपतित है। इस झिरी से पर्याप्त दूरी पर एक प्रतिदीप्त पर्दा रखा है। यदि, इलेक्ट्रॉनों की चाल को बढ़ा दिया जाए तो, निम्नांकित में से कौन-सा कथन सत्य होगा ?
- 69यंग वु एक द्विझिरी प्रयोग में झिरियों $($स्लिटों$)$ के बीच की दूरी $2\ mm$ है। इनको $\lambda_1=12000 A$ तथा $\lambda_1=$ $10000 A$ तरंगदैर्ध्य के फोटॉनों से प्रदीप्त $($प्रकाशित$)$ किया गया है। यदि झिरियों से पर्दे की दूरी $2 m$ हो तो, केन्द्रीय दीप्त फ्रिंज के कितनी न्यूनतम दूरी पर, व्यतिकरण के उत्पन्न दोनों तरंगों की दीप्त फ्रिंजें संपाती $($एक दूसरे के ऊपर$)$ होगी?View Solution
- 70एक कागज जिस पर दो निशान $d$ दूरी पर बने हैं एक व्यक्ति की दृष्टि की आँख के लेन्स का व्यास $2$ मिमी है। $d$ के किस न्यूनतम मान के लिए ये दोनों निशान अलग अलग दिखायी देगें? दृश्य प्रकाश की माध्य तरंग दैर्ध्य $5000 A$ है।View Solution
- 71View Solutionनिम्न में से कौन सा कणिक प्रकृति पर आधारित है?
- 72View Solutionप्रकाश तंतु में प्रकाश के आगे चलने का कारणः
- 73View Solutionसाबुन के बुलबुले का रंगीन होना किसे संकेत करता है?
- 74View Solutionफ्रेसनैल द्विप्रिज्म में लेंस की स्थिति 16 मीटर तथा 9 सेमी पर है। उनके बीच वास्तविक दूरी होगी?
- 75View Solutionव्यतिकरण कक्ष में जब हवा थी तो व्यतिकरण दिखायी दिया यदि कक्ष में निर्वात कर दिया जाये तथा प्रकाश स्रोत्र पहले जैसा ही हो तो
- 76$5000 A$ वाले समान्तर एकवर्णी प्रकाश $0.001$ मीटर मोटाई की स्लिट पर लम्बवत डाला जाता है । प्रकाश को एक उत्तल लेंस के द्वारा एक स्क्रीन पर एकत्र किया जाता है। पहली निम्नतम के लिए विवर्तन कोण का मान होगाःView Solution
- 77View Solutionयंग प्रयोग में सोडियम लैम्प की पीली रोशनी को एकवर्णी नीली रोशनी से बदला जाता है जिसकी तीव्रता समान है। तो
- 78यंग का प्रयोग $\lambda=5000 A$ वाले प्रकाश के लिए किया जाता है। दो स्लियों के बीच की दूरी $0.2$ मिमी तथा स्क्रीन की दूरी $200$ सेमी है । केन्द्र से तीसरे उच्चतम की दूरी होगी.View Solution
- 79View Solutionएक एकवर्णी प्रकाश की तरंग निर्वात से अपवर्तनांक 1. 5 वाले माध्यम में आपतित होती है। अपवर्तित प्रकाश की तरंग दैर्ध्य होगी:
- 80दो किरणों की तीव्रता का अनुपात $4: 1$ है । इनके आयामों का अनुपात होगा :View Solution
- 81यंग के प्रयोग में दो कोहैरेन्ट स्रोत्र $0.90$ मिमी की दूरी पर रखे हैं । यदि ये दूसरी डार्क फ्रिंज 1 मीटर पर बनाते हों तो एकवर्णी प्रकाश की तरंग दैर्ध्य होगी :View Solution
- 82यंग के प्रयोग में फ्रिंज की चौडाई $0.4$ मिमी है । यदि पूरे उपकरण को $4 / 3$ अपवर्तनांक के पानी में डुबो दिया जाए तो नयी फ्रिंज चौड़ाई होगी-View Solution
- 83यंग के प्रयोग नीले तथा हरे प्रकाश तरंग दैर्ध्य $4360 A$ के लिए किया गया है। यदि केन्द्र से चौथे उच्चतम की दूरी $x$ है तोView Solution
- 84View Solutionव्यतिकरण संभव है:
- 85View Solutionनिम्न में से कौन सा हाइगेंस सिद्धान्त पर आधारित नहीं हैं?
- 86View Solutionनिम्न से कौन सा ध्वनि तथा प्रकाश दोनों तरंगों में नहीं होता?
- 87जब किसी धात्विक पृप्ठ को तरंगदैर्ध्य $\lambda$ के विकिरणों से प्रदीप्त किया जाता है, तो निरोधी विभव $V$ है। यदि इसी पृप्ठ को तरंगदैर्ध्य $2 \lambda$ के विकिरणों से प्रदीप्त किया जाए, तो निरोधी विभव $\frac{ V }{4}$ हो जाता है। इस धात्विक पृप्ट की देइली तरंगदैर्ध्य है :View Solution
- 88द्रव्यमान $m$ के इलेक्ट्रॉन तथा किसी फोटॉन की ऊर्जाएं $E$ एकसमान हैं। इनसे संबद्न दे$-$ब्बाग्ती तरंगदैर्घ्यों का अनुपात है :View Solution
$($यहाँ $c$ प्रकाश का वेग है।$)$ - 89किसी प्रकाशवैन्युत पृप्ठ को क्रमश: $\lambda$ तथा $\frac{\lambda}{2}$ तरंगदैर्ध्य के एकवर्णी प्रकाश से प्रदीप्त किया जाता है। यदि उत्सर्जित प्रकाश विद्युत इललोक्ट्रॉनो की अधिकतम गतिज ऊर्जा का मान, दूसरी दशा में पहली दशा से $3$ गुना है, तो इस पृष्ट के पदार्थ का कार्य फलन है:View Solution
$( h =$ प्लांक स्थिरांक$, c =$ प्रकाश का वेग$)$ - 90किसी धातु का कार्य फलान $2.28\ eV$ है। इस पर $500\ nm$ तरंगदैर्घ्य का प्रकाश आपतित होता है तो, उत्सर्जित इलेक्ट्रॉन की दे$-$ब्रॉग्ली तरंगदैर्घ्य होगीView Solution
- 91View Solutionयदि किसी कण की गतिज उर्जा को उसके प्रारम्भिक मान से 16 गुना कर दिया जाये तो, संगत दे-ब्रॉग्ली तरंगों की तरंगदैर्ध्य में प्रतिशत परिवर्तन होगा
- 92धातु के किसी पृष्ठ पर आपतित विकिरणों की ऊर्जा को $20 \%$ बढ़ाने पर, उससे उत्सर्जित फोटो इलेक्ट्रॉनों $($प्रकाश विद्युत इलेक्ट्रॉनों$)$ की गतिज उर्जा $0.5\ eV$ से बढ़कर $0.8\ eV$ हो जाती है। इस धातु का कार्य फलन हैView Solution
- 93यदि किसी इलेक्ट्रॉन और फोटॉन की ऊर्जा $( E )$ है और उनकी तरंगदैर्ध्य क्रमश $\lambda_{ e }$ तथा $\lambda_{ p }$ हों तो, इनवु बीच संबंध होगा:View Solution
- 94किसी धातु से प्रकाश विद्युत उत्सर्जन के लिए निरोधी (अंतक) आवृत्ति $v$ है। यदि इस धातु पर $2 v$ आवृत्ति के विकिरण आपतित हों तो, उत्सर्जित इलेक्ट्रॉनों का अधिकतम संभावित वेग होगा: ( $m$ इलेक्ट्रॉन का द्रव्यमान है।)View Solution
- 95किसी इलेक्ट्रॉन के संवेग को $P$ से परिवर्तन करने पर उससे संबद्व दे-ब्रोग्ली तरंगदैर्ध्य $0.5 \%$ परिवर्तित हो जाती है। इलेक्ट्रॉन का प्रारंभिक संवेग होगा :View Solution
- 96क्रमशः $1 eV$ तथा $2.5 eV$ ऊर्जा के फोटॉन विकिरण एक के बाद एक किसी प्रकाश सुग्राही (संवेदी) पृष्ठ को प्रदीप्त करते हैं। इस पृष्ठ का कार्य फलन $0.5 eV$ है। इन दोनों में उत्सार्जित इलेक्ट्रॉनो की अधिकतम चालों का अनुपात होगा :View Solution
- 97$0.25\ Wb / m ^2$ तीव्रता के चुम्बकीय क्षेत्र की उपस्थिति में एक $\alpha-$कण $0.83 \ cm$ त्रिज्या के वृत्ताकार पथ में गति करता है तो, इस कण से सम्बद्ध दे $-$ ब्रॉग्ली तरंगदैध्ध्य होगी :View Solution
- 98$200 W$ का एक सोडियम बल्ब $0.6 \ \mu m$ तरंगदैर्ध्य का पीला प्रकाश उत्सर्जित करता है। यह मानते हुए कि विद्युत ऊर्जा को प्रकाश में परिवर्तन करने में बल्ब की दक्षता $25 \%$ है, प्रति सेकण्ड उत्सर्जित पीले रंग के प्रकाश के फोटॉनों की संख्या होगी:View Solution
- 99एक इलेक्ट्रान, हाइड्रोजन परमाणु की प्रथम उत्तेजित अवस्था से उसकी निम्नतम अवस्था में संक्रमण करता है। इससे उत्सर्जित एकवर्णी विकिरण किसी प्रकाश सुग्राही पदार्थ को किरणित करता है। इसका निरोधी विभव $3.57 V$ मापा गया है। इस पदार्थ की देहली आवृत्ति है :View Solution
- 100किसी हाइड्रोजन परमाणु में एक इलेक्ट्रॉन उत्तेजित अवस्था $n$ से न्यूनतम ऊर्जा स्थिति में संक्रमण करता है (कूदता) है। इससे विकिरित तरंगदैर्ध्य का प्रकाश एक ऐसे प्रकाशसंवेदी पदार्थ को प्रदीप्त करता है जिसका कार्यफलन $2.75 eV$ है। यदि प्रकाश विद्युत इलेक्ट्रॉनों का निरोधी (अंतक) विभव $10 V$ है तो $n$ का मान होगा:View Solution