Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1किसी धातु से प्रकाश विद्युत उत्सर्जन के लिए निरोधी (अंतक) आवृत्ति $v$ है। यदि इस धातु पर $2 v$ आवृत्ति के विकिरण आपतित हों तो, उत्सर्जित इलेक्ट्रॉनों का अधिकतम संभावित वेग होगा: ( $m$ इलेक्ट्रॉन का द्रव्यमान है।)View Solution
- 2किसी इलेक्ट्रॉन के संवेग को $P$ से परिवर्तन करने पर उससे संबद्व दे-ब्रोग्ली तरंगदैर्ध्य $0.5 \%$ परिवर्तित हो जाती है। इलेक्ट्रॉन का प्रारंभिक संवेग होगा :View Solution
- 3क्रमशः $1 eV$ तथा $2.5 eV$ ऊर्जा के फोटॉन विकिरण एक के बाद एक किसी प्रकाश सुग्राही (संवेदी) पृष्ठ को प्रदीप्त करते हैं। इस पृष्ठ का कार्य फलन $0.5 eV$ है। इन दोनों में उत्सार्जित इलेक्ट्रॉनो की अधिकतम चालों का अनुपात होगा :View Solution
- 4$0.25\ Wb / m ^2$ तीव्रता के चुम्बकीय क्षेत्र की उपस्थिति में एक $\alpha-$कण $0.83 \ cm$ त्रिज्या के वृत्ताकार पथ में गति करता है तो, इस कण से सम्बद्ध दे $-$ ब्रॉग्ली तरंगदैध्ध्य होगी :View Solution
- 5$200 W$ का एक सोडियम बल्ब $0.6 \ \mu m$ तरंगदैर्ध्य का पीला प्रकाश उत्सर्जित करता है। यह मानते हुए कि विद्युत ऊर्जा को प्रकाश में परिवर्तन करने में बल्ब की दक्षता $25 \%$ है, प्रति सेकण्ड उत्सर्जित पीले रंग के प्रकाश के फोटॉनों की संख्या होगी:View Solution
- 6एक इलेक्ट्रान, हाइड्रोजन परमाणु की प्रथम उत्तेजित अवस्था से उसकी निम्नतम अवस्था में संक्रमण करता है। इससे उत्सर्जित एकवर्णी विकिरण किसी प्रकाश सुग्राही पदार्थ को किरणित करता है। इसका निरोधी विभव $3.57 V$ मापा गया है। इस पदार्थ की देहली आवृत्ति है :View Solution
- 7किसी हाइड्रोजन परमाणु में एक इलेक्ट्रॉन उत्तेजित अवस्था $n$ से न्यूनतम ऊर्जा स्थिति में संक्रमण करता है (कूदता) है। इससे विकिरित तरंगदैर्ध्य का प्रकाश एक ऐसे प्रकाशसंवेदी पदार्थ को प्रदीप्त करता है जिसका कार्यफलन $2.75 eV$ है। यदि प्रकाश विद्युत इलेक्ट्रॉनों का निरोधी (अंतक) विभव $10 V$ है तो $n$ का मान होगा:View Solution
- 8किसी प्रकाश सुग्राही धातु के लिये, देहली आवृत्ति $3.3 \times 10^{14} Hz$ है। यदि इस धातु पर $8.2 \times 10^{14} Hz$ आवृत्ति का प्रकाश आपतित हो तो प्रकाश विद्युत उत्सर्जन के लिए निरोधी $($अन्तक$)$ वोल्टता होगी, लगभगःView Solution
- 9किसी धातु का कार्य फलन $1.8 eV$ है। इससे प्रकाश विद्युत उत्सर्जन में उत्पन्न इलेक्ट्रॉनों की अधिकतम ऊर्जा $0.5 eV$ है। इसका संगत निरोधी (अंतक) विभव होगा:View Solution
- 10View Solutionडेविसन और जर्मर के प्रयोग में 'इलेक्ट्रॉन गन,' द्वारा उत्सर्जित इलेक्ट्रोनों के वेग को बढ़ाया जा सकता है:
- 11किसी इलेक्ट्रॉन सूक्ष्मदर्शी में प्रयुक्त इलेक्ट्रॉनों को $25\ kV$ की वोल्टता से त्वरित किया जाता है। यदि वोल्टता को बढ़ा कर $100\ kV$ कर दिया जाये तो इलेक्ट्रॉनों से संबद्ध डी$-$ब्रोग्ली तरंगदैर्ध्य का मान :View Solution
- 12View Solutionप्रकाश विद्युत उत्सर्जन होने के लिए यह आवश्यक है कि आपतित प्रकाश की एक निश्चित न्यूनतम मान से अधिक
- 13दो भिन्न आवृत्तियों के प्रकाश जिनके फोटॉन की ऊर्जा क्रमश: $1\ eV$ और $2.5\ eV$ है, किसी ऐसे धातु पृष्ठ को एक के बाद एक प्रदीप्त करते हैं जिसका कार्य फलन $0.5\ eV$ है, तो उत्सर्जित इलेक्ट्रॉनों की अधिकतम चालों का अनुपात होगा:View Solution
- 14जब $I$ तीव्रता के एकवर्णी विकिरण, किसी धातु की सतह पर टकराते हैं तो, फोटॉनों की संख्या और उनकी अधिकतम गतिज ऊर्जा क्रमशः $N$ और $T$ है। यदि विकिरणों की तीव्रता $2 I$ हो तो उत्सर्जित इलेक्ट्रॉनों की संख्या और उनकी अधिकतम गतिज ऊर्जा क्रमशः होंगेView Solution
- 15निकैल का कार्य फलन $5.01 eV$ है। इसके पृष्ठ पर 200 $n m$ तरंगदैर्ध्य के पराबैंगनी प्रकाश आपतित होता है। सबसे द्रुतगामी उत्सर्जित प्रकाशिक इलेक्ट्रॉन को रोकने के लिए आवश्यक विभवान्तर होगाView Solution
- 16एक स्त्रोत $S_1$ प्रति सेकंड $5000 A$ तरंगदैध्ध्य के $10^{15}$ फोटॉन उत्पन्न करता है। एक अन्य स्त्रोत $S_2, 5000 A$ तरंगदैर्ध्य के $1.02 \times 10^{15}$ फोटॉन प्रति सेकण्ड उत्पन्न करता है, तो $\left(S_2\right.$ की शक्ति) $/\left(S_1\right.$ की शक्ति) का मान होगाView Solution
- 17एक $p - n$ फोटोडायोड को बैन्ड गैप (अन्तराल) $2.5 eV$ के अर्धचालक से बनाया गया है। यह किस तरंग दैर्ध्य के संकेत का संसूचन कर सकता है:-View Solution
- 18देहली आवृत्ति $\left(v_0\right)$ से अधिक आवृत्ति $(v)$ के प्रकाश द्वारा उत्सर्जित इलैक्ट्रानों की संख्या अनुपाती होती है:-View Solution
- 19हीलियम नीयॉन लेजर $667\ nm$ तरंग दैर्ध्य का प्रकाश उत्पन्न करता है। उत्सर्जित शक्ति $9\ mW$ है। इस प्रकाश पुंज द्वारा प्रकाशित लक्ष्य पर प्रति सैकण्ड पहुँचने वाले इलैक्ट्रॉनों की मध्यमान संख्या होगी $:-$View Solution
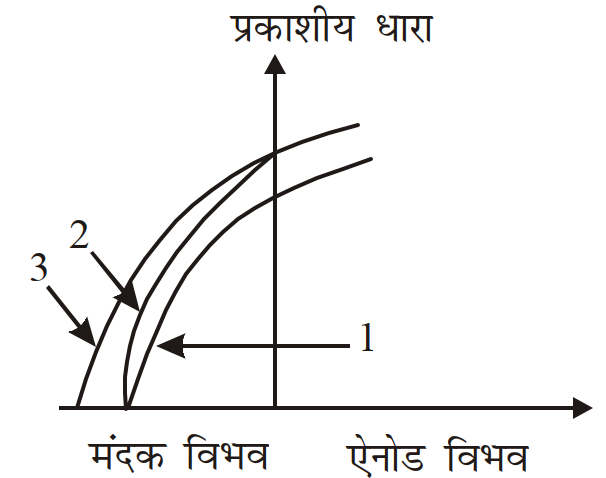
- 20View Solutionइस चित्र में एक प्रकाश सुक्रीय तल पर तीन विभिन्न विकिरणों के लिये प्रकाशीय धारा और ऐनोड विभव के बीच आरेखों को दिखाया गया है। निम्न कथनों में से किस को यथार्थ माना जायेगा?
- 21एक मिलीग्राम द्रव्यमान का एक गतिशील कण उतना ही तरंगदैर्ध्य रखता है जितना की $3 \times 10^6\ ms ^{-1}$ चाल से चलने वाला इलेक्ट्रॉन। कण की चाल होगी:View Solution
$($इलैक्ट्रान का द्रव्यमान $=9.1 \times 10^{-31} \ kg )$ - 22View Solutionकम दाब पर गैसों में विद्युत विसर्जन के प्रक्रम में टयूब में रंगदार चमक उत्पन्न होने का कारण होता है:
- 23एक प्रकाश सक्रिय पदार्थ के तल का कार्य फलन $6.2\ eV$ है। यदि स्टोपिंग$-$विभव $5V$ हो तो उत्सर्जित इलेक्ट्रॉन का तरंगदैध्य्य पड़ेगा :View Solution
- 245 वाट का एक स्त्रोत $5000 A$ तरंगदैध्ध्य के एकवर्णी प्रकाश का उत्सर्जन करता है। $0.5$ मी की दूरी पर रखने से यह एक प्रकाश संवेदी धात्विक तल से प्रकाशी इलेक्ट्रॉन मुक्त करता है। जब स्त्रोत को तल से $1.0$ मी की दूरी पर ले जाया जायेगा तो विमुक्त प्रकाशी इलेक्ट्रॉनों की संख्याView Solution
- 25एक लेसर द्वारा $6.0 \times 10^{14} Hz$ आवृत्ति का एकवर्णी प्रकाश पैदा किया जाता है। उत्सर्जित शक्ति $2 \times 10^{-3} W$ है। स्त्रोत से प्रति सेकेण्ड उत्सर्जित फोटानों की औसत संख्या होगी-View Solution
- 26$1\ MeV$ ऊर्जा वाले फोटॉन का संवेग किग्रा/सेकण्ड में हैView Solution
- 27View Solutionएक प्रकाश-वैद्युत सैल में प्रकाश वैद्युत प्रभाव बदलता है
- 28जब एल्यूमिनियम प्लेट पर $hv$ ऊर्जा वाले फोटॉंन डाले जाते हैं $($कार्यफलन $E _0 )$ तो अधिकतम गति वाले इलैक्ट्रान की गतिज ऊर्जा $K$ है। यदि डाले गये विकिरण की आवृत्ति दोगुनी कर दी जाए तो निकले फोटो इलैक्ट्रान की अधिकतम गतिज ऊर्जा होगीView Solution
- 29View Solutionएक डिस्चार्ज नलिका में गैसों के आयनीकरण का कारण निम्न कणों का संघट्ट है
- 30एक धातु का कार्यफलन $hv v _0$ है। यदि इस पर $2 hv _0$ की ऊर्जा का प्रकाश डाला जाए तो $4 \times 10^6$ मी/सेकण्ड की गति वाले इलैक्ट्रान बाहर निकलते हैं। यदि $5 h v_0$ ऊर्जा वाली प्रकाश डाले जाए तो निकले इलैक्ट्रान की अधिकतम गतिज ऊर्जा हैView Solution
- 31तीन धातुओं $A , B$ एवं $C$ के कार्यफलन क्रमशः $1.92\ eV$, $2.0\ eV$ एवं है। आंइस्टीन समी. के अनुसार $4100 A$ की तरंगदैध्ध्य से कौन से धातु से फोटोइलेक्ट्रान निकलेंगेंView Solution
- 32हाइड्रोजन अणु की ऊर्जा, मुख्य क्वाण्टम संख्या के साथ $E =-\frac{13.6}{ n ^2} eV$ है। यदि एक इलैक्ट्रान $n =3$ से $n =2$में कूत्ता है तो निकले फोटोंन की ऊर्जा है:View Solution
- 33View Solutionप्रकाश-वैद्युत प्रभाव में आवृत्ति तथा गतिज ऊर्जा का ग्राफ होगा
- 34एक प्रकाश विद्युत सैल को $1 m$ दूरी किसी प्रकाश स्त्रोत से चमकाया जाता है यदि प्रकाश स्रोत को $2 m$ दूर ले जाएँ तो :View Solution
- 35View Solutionजब किसी धातु पर पराबंगनी विकिरण गिरता है तो फोटो इलैक्ट्रॉन निकलते हैं। ये है
- 36View Solutionनिम्न में से कौन-सा कथन कैथोड किरणों के लिए सत्य है?
- 37View Solutionकिस निम्न किस गतिज कण (समान वेग से गतिशील) की तरंग दैर्ध्य अधिकतम है:
- 38View Solutionआंइस्टीन ने प्रकाश वैद्युत प्रभाव पर किस समीकरण का समर्थन किया?
- 39View Solutionयदि प्रकाश की तीव्रता को बढ़ा दी जाए तो
- 40एक धातु प्लेट का कार्यफलन $4.125 \ eV$ है। तो इसकी देहली तरंगदैर्ध्य होगीView Solution
- 41एक प्रकाश$-$वैद्युत सेल में $\lambda$ तरंग$-$दैर्ध्य का प्रकाश डालने पर इलैक्ट्रॉन की सर्वाधिक गति $v$ है, तो तरंगदैर्ध्य $3 \lambda / 4$ करने से सर्वाधिक गति होगीView Solution
- 42$5000 A$ तंरग दैर्ध्य वाला प्रकाश एक कैथोड प्लेट पर पड़ा। इसका कार्य फलन $1.9 eV$ है। फोटो इलैक्ट्रॉन की गतिज ऊर्जा है-View Solution
- 43हाइड्रोजन के हाइपरफाईन इनटरैक्शन से $21 cm$ की रेडियो किरणें विकिरित होती हैं। विकिरित किरणों की ऊर्जा हैView Solution
- 44View Solutionकांस्मिक किरणें है:
- 45View Solutionनिम्न में से कौन-सा तथ्य ठीक है-
- 46एक इलैक्ट्रॉन $100\ V$ विभव से त्वरित किया जाता है तो इसकी संबंधित तरंगदैध्य होगी$-$View Solution
- 47एक इलैक्ट्रॉन जिसका द्रव्यमान $m$ तथा आवेश $e$ है, को $V$ विभव देकर त्वरित किया गया। इसका अंतिम वेग होगाView Solution
- 48एक धातु की देहली तरंगदैर्ध्य $2000 A$ है, इसका कार्य फलन होगाView Solution
- 49एक इलैक्ट्रॉन $100 V$ पर त्वरित होता है तो उसकी गतिज ऊर्जा हैView Solution
- 50किसी धातु का कार्यफलन $3.5 eV$ है। निकले हुए इलैक्ट्रान को रोकने के $-1.2 V$ विभव लगाना पड़ता है तोView Solution
- 51$He ^{++}$तथा $H ^{+}$को समान वोल्ट का विभव देकर वितामावस्था से त्वरित अर्जित किया गया। $He ^{++}$तथा $H ^{+}$के अंतिम वेगों का अनुपात बताओ-View Solution
- 52View Solutionफोटो-इलैक्ट्रिक सेल के कैथोड पर 300 नैनो मीटर तरंगदैर्ध्य का प्रकाश डाला जाता है तो फोटोइलैक्ट्रान निकलते हैं। जबकि दूसरे सेल के लिए यही काम 600 नैनो मीटर तरंगदैध्ध्य से होता है। दोनों के कार्यफलनों की तुलना करो।
- 53View Solutionनिकले हुए फोटो इलैक्ट्रॉन की संख्या बढ़ेगी यदि
- 54एक फोटॉन जिसकी तरंगदैध्ध्य $\lambda$ हो उसका संवेग हैView Solution
- 55एक प्रकाश वैद्युत सैल का कैथोड बदलने से उसका कार्य फलन $W _1$ से $W _2$ बदल जाता है $\left( W _2> W _1\right)$ ) बिना किसी परिवर्तन के पहले धारा का मान $I _1$ तथा बाद में $I _2$ है तो $\left(\right.$ माना $h v> W _2$ )View Solution
- 56एक आयनीकरण बॉक्स में दो समान्तर प्लेट एनोड तथा कैथोड जिन पर $5 \times 10^7$ इलैक्ट्रॉन है। इतना ही एनोड के पास सिंगल आवेशित धनात्मक आवेश प्रति सेमी$^3$ में है इलैक्ट्रॉन एनोड की तरफ $0.4$ मी/सेकण्ड से भागते हैं तो एनोड पर धारा घनत्व $4$ माइक्रो एम्पियर / मी$^2$ होता है। धनात्मक आवेश की चाल होगी $-$View Solution
- 57$1 keV$ ऊर्जा वाले फोटॉन की तरंगदैर्ध्य $1.24 \times 10^{-9}$ मी है। तो $1 MeV$ फोटॉन की आवृत्ति क्या है?View Solution
- 58किसी धातु पर $3000 A$ की तरंगदैर्ध्य वाला प्रकाश डाला जाता है तो फोटो इलैक्ट्रान किस गति से निकलेंगे जबकि कार्य फलन $1\ eV$ है।View Solution
- 59एक रेडियो ट्रांसमीटर $880\ kHz$ तथा $10\ kW$ पर कार्य करता है। प्रति सेकण्ड कितने फोटॉंन निकलेंगे $-$View Solution
- 60एक विद्युत चुम्बकीय विकिरण के फोटॉंन का संवेग है। $3.3$ $\times 10^{-29}\ kgm / sec$ इसकी संबंधित आवृत्ति है:View Solution
$\left( h =6.6 \times 10^{-34} Js ; c =3 \times 10^8 ms ^{-1}\right. )$ - 61एक अणु के ऊर्जा स्तर $A , B , C$ बढ़ते क्रम मे है अर्थार्त $E _{ A }< E _{ B }< E _{ C }$ यदि $\lambda_1, \lambda_2, \lambda_3$ क्रमशः $C$ से $B , B$ से $A$ तथा $C$ से $A$ संक्रमण संबंधित तरंगदैध्ध्य हो, तो कौन-सा संबंध सत्य है?View Solution
- 62हाइड्रोजन अणु के बोर मॉंडल में एक इलैक्ट्रॉन माना $n ^{\text {th }}$ कक्षक में है। इस कक्षा की परिधि को डी-ब्रागली तरंगदैर्ध्य $\lambda$ के पद मे व्यक्त किया जा सकता हैView Solution
- 63एक कण का द्रव्यमान $m$ तथा वेग $v$ है इससे संबंधित डी-ब्राग्ली तरंगदैध्य का मान हैView Solution
- 64$6.2 \ eV$ के पराबंगनी विकिरण एल्यूमिनियम पर गिरते हैं। तो सबसे अधिक गति वाले इलैक्ट्रान की $K.E.$ है $(W= 4.2\ eV)$View Solution
- 65किसी फोटॉन की ऊर्जा जबकि उसकी तरंगदैर्ध्य $\lambda$ हो तो-View Solution
- 66फोटोइलैक्ट्रिक प्रभाव में $Na$ की देहली आवृत्ति से संबंधित तंरंगदैर्ध्य $5000 A$ है तो कार्य-फलन हैView Solution
- 67जब द्रव्यमान ' $m$ ' तथा वेग ' $v$ ' से गतिमान कोई $\alpha$ कण 'Ze' आवेश के किसी भारी नाभिक पर बमबारी करता है, तो उसकी नाभिक से निकटतम उपगमन की दूरी, $m$ पर इस प्रकार निर्भर करती है :View Solution
- 68रिडबर्ग नियतांक का मान $10^7 m ^{-1}$ दिया गया है? हाइड्रोजन स्पेक्ट्रम की बामर श्रेणी की अंतिम लाइन की तरंग संख्या होगी:View Solution
- 69View Solutionहाइड्रोजन के स्पेक्ट्रम में, लाइमन तथा बामर श्रेणियों की दीर्घतम तरंगदैर्य्यो का अनुपात होता है
- 70निम्नतम ऊर्जा स्थिति में हाइड्रोजन परमाणु को $975 A$ तरंगदैर्ध्य के एकवर्णी प्रकाश से उत्तेजित किया जाता है तो, परिणामी स्पैक्ट्रम में स्पैक्ट्रम रेखाओं की संख्या होगीView Solution
- 71View Solutionहाइड्रोजन के स्पेक्ट्रम में लाइमन तथा बामर श्रेणी की सर्वाधिक लम्बी तरंगदैध्यों का अनुपात होगा हैः
- 72हाइड्रोजन के समान किसी परमाणु में $n=3$ अवस्था से $n=1$ अवस्था में संक्रमण से पराबैगनी विकिरणों का उत्सर्जन होता है। इसी परमाणु में अवरक्त किरणों का उत्सर्जन होगा यदि संक्रमण हो :View Solution
- 73किसी अचल हाइड्रोजन परमाणु का एक इलेक्ट्रॉन पाँचवें ऊर्जास्तर से न्यूनतम अवस्था स्तर को गमन करता है तो, फोटॉन उत्सर्जन के परिणामस्वरूप परमाणु द्वारा प्राप्त वेग होगा :View Solution
(जहाँ $m$ इलेक्ट्रॉन का द्रव्यमान, $R$, रिडबर्ग नियतांक और $h$ प्लांक नियतांक है।) - 74किसी हाइड्रोजन परमाणु में एक इलेक्ट्रॉन, पहले तृतीय उत्तेजित अवस्था से द्वितीय उत्तेजित अवस्था में, और फिर द्वितीय उत्तेजित अवस्था से प्रथम उत्तेजित अवस्था में संक्रमण करता है। इन दो दशाओं में उत्सर्जित तरंगदैध्य्यो का अनुपात $\lambda_1: \lambda_2$ होगा :View Solution
- 75किसी हाइड्रोजन परमाणु में एक इलेक्ट्रॉन उत्तेजित अवस्था $n$ से न्यूनतम ऊर्जा स्थिति में संक्रमण करता है (कूदता) है। इससे विकिरित तरंगदैर्ध्य का प्रकाश एक ऐसे प्रकाशसंवेदी पदार्थ को प्रदीप्त करता है जिसका कार्यफलन $2.75 eV$ है। यदि प्रकाश विद्युत इलेक्ट्रॉनों का निरोधी (अंतक) विभव $10 V$ है तो $n$ का मान होगा:View Solution
- 76View Solutionहाइड्रोजन परमाणु के बोर के मॉडल के अनुसार, निम्नलिखित में से कौन, हाइड्रोजन परमाणु द्वारा उत्सर्जित फोटॉन की संभावित ऊर्जा नहीं है?
- 77हाइड्रोजन परमाणु की लाइमन श्रेणी की प्रथम लाईन की तरंगदैर्ध्य, किसी हाइड्रोजन के समान आयन की बामर श्रेणी की द्वितीय लाईन के बराबर है, तब हाइड्रोजन के समान आयन की परमाणु संख्या $Z$ होगी:View Solution
- 78$\frac{1}{2} m v^2$ ऊर्जा का एक अल्फा कण-नाभिक, $Z e$ आवेश के एक भारी नाभिकीय लक्ष्य पर टकराता है। अल्फा-नाभिक के लिये समीपतम पहुँचने की दूरी, निम्नांकित में किसके अनुक्रमानुपाती होगी?View Solution
- 79हाइड्रोजन परमाणु की निम्नतम अवस्था स्थिति में उर्जा $-13.6 eV$ है। $He ^{+}$आयन की प्रथम उत्तेजित अवस्था में उर्जा होगीView Solution
- 80रदरफोर्ड के प्रकीर्णन प्रयोग में जब आवेश $Z_1$ और द्रव्यमान $M _1$ का प्रक्षेप्य आवेश $Z _2$ और द्रव्यमान $M _2$ के लक्ष्य केन्द्रक तक पहुँचता है तो निकटतम पहुँच की दूरी $I _0$ होती है। प्रक्षेप्य की ऊर्जा :-View Solution
- 81हाइड्रोजन परमाणु की आद्य अवस्था में इलैक्ट्रॉन की आयनन ऊर्जा $13.6 \ eV$ होती है। $6$ तरंग दैर्ध्य की तरंगों की विकिरणों के उत्सर्जन के लिए परमाणुओं को ऊपरी ऊर्जा स्तरों तक उत्तेजित किया जाता है। उत्सर्जित विकिरण का अधिकतम तरंग दैर्ध्य इनमें से किस स्थिति परिर्वतन से सम्बन्धित होगा $:-$View Solution
- 82हाइड्रोजन परमाणु की आद्य अवस्था की ऊर्जा $-13.6 \ eV$ है। जब इसका इलेक्ट्रान प्रथम उत्तेजित अवस्था में होगा, तो इसकी उत्तेजन ऊर्जा होगी :View Solution
- 83हाइड्रोजन परमाणु की आद्य अवस्था में इलेक्ट्रॉन की पूर्ण ऊर्जा $-13.6\ eV$ होती है। प्रथम उत्तेजित अवस्था में इलेक्ट्रॉन की गतिज ऊर्जा होगी $-$View Solution
- 84हाइड्रोजन अणु का आयनीकरण विभव $13.6 eV$ है। निम्न स्तर के हाड्रोजन अणु को उत्तेजित स्तर में लाने हेतु $12.1 eV$ ऊर्जा वाला फोटॉन डालना पड़ता है। बोर सिद्धान्त के अनुसार स्पैक्ट्रम लाइनों की संख्या होगीView Solution
- 85हाइड्रोजन अणु की पहली उत्तेजित अवस्था में कुल ऊर्जा $-3.4 eV$ है तो इसी अवस्था में गजित ऊर्जा बताओView Solution
- 86View Solutionबोर का अणु मोंडल
- 87View Solutionजे.जे थॉंमसन का कैथोड ट्यूब प्रयोग बताता है कि
- 88View Solutionकौन से कणों के लिए पहले आर्बिट की त्रिज्या निम्नतम होगी।
- 89एक इलैक्ट्रॉन कक्षा $n =2$ से $n =4$ में जाता है तो विकिरण की तरंग दैर्ध्य है $( R =$ रिडबर्ग नियतांक$)$View Solution
- 90एक हाइड्रोजन अणु के $n ^{\text {th }}$ कक्षक की ऊर्जा $E _{ n }$ हो तो $He ^{+}$के $n ^{\text {th }}$ कक्षक की ऊर्जा हैView Solution
- 91View Solutionइलैक्ट्रॉन के आवेश की गणना कर किसने अप्रत्यक्ष रूप से इलैक्ट्रॉन के द्रव्यमान का पता लगाया
- 92View Solutionनिम्न में से किस विकिरण का हाइड्रोजन अणु सर्वाधिक आवृत्ति वाला फोटॉन देगा
- 93View Solutionजब एक इलैक्ट्रॉन चौथे कक्षक से दूसरे कक्षक में कदता है तो मिलेगी
- 94हाइड्रोजन के बोर मॉडल मे अभिकेन्द्र बल तथा प्रोटॉन व इलैक्ट्रॉन के बीच लगने वाला कूलॉम बल एक दूसरे को संतुलित करते हैं। यदि $a_0$ निम्न स्तर की कक्षा की त्रिज्या, $m$ इलैक्ट्रान का द्रव्यमान, $e$ आवेश तथा $\varepsilon_0$ विद्युतशीलता हो तो इलैक्ट्रान का वेगView Solution
- 95View Solutionहाइड्रोजन अणु की पहली उत्तेजित अवस्था में त्रिज्या होगी
- 96View Solutionजब हाइड्रोजन अणु निम्न स्तर से उत्तेजित स्तर पर पहुंचता है तो
- 97View Solutionसोडियम वाष्प लैम्प से जो स्पैक्ट्रम मिलेगा वह उदाहरण है
- 98निम्न स्तर पर $H _2$ अणु की त्रिज्या $5.3 \times 10^{-11}$ मी है। एक इलैक्ट्रॉन के टकराने से त्रिज्या $21.2 \times 10^{-11}$ मी हो जाती है। मुख्य क्वाण्टम संख्या होगी $-$View Solution
- 99रद्रफोर्ड के $\alpha-$ प्रयोग में सही कोण क्या होगा यदि इम्पैक्ट पैरामीटर ज्ञात करना हो, $b =0$ ?View Solution
- 100View Solutionकौन सा स्रोत लाइन-उत्सर्जन स्पैक्ट्रम बनाता है?