Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1एक कृष्णिका का ताप $500 K$ है। इससे ऊर्जा उत्सर्जन की दर समानुपाती होगी:View Solution
- 2पीतल तथा स्टील का रेखीय प्रसार गुणांक $\alpha_1$ तथा $\alpha_2$ है । पीतल की छड़ की लम्बाई $\ell_1$ तथा स्टील की $\ell_2$ $0^{\circ} C$ तापमान पर है । यदि इनकी लम्बाइयों में अन्तर सभी तापमान पर $\ell_2-\ell_1$, हो तो:View Solution
- 3एक बीकर में गर्म पानी भरा गया है। इसे किसी कमरे में रखा जाता है। यदि इसका ताप $80^{\circ} C$ से $75^{\circ} C t _1$ मिनट में, $75^{\circ} C$ से $70^{\circ} C t _2$ मिनट में होता हो तथा $70^{\circ} C$ से $65^{\circ} C$ तक $t _3$ मिनट में होता है तो:View Solution
- 4एक पिण्ड $50.0^{\circ} C$ से $49.9^{\circ} C$ तक ठण्डा होने में 5 सेकंड लेता है तो यह $40.0^{\circ} C$ से $39.9^{\circ} C$ तक ठण्डा होने में कितना समय लेगा । बाहर का तापमान $30.0^{\circ} C$ तथा यहाँ न्यूटन का शीतलन सिद्धान्त कार्यरत् है।View Solution
- 5View Solutionयदि सूर्य का तापमान दोगुना हो जाए तो पृथ्वी पर आने पर ऊर्जा कितने गुणा बढ़ेगी?
- 6View Solutionपारे का थर्मामीटर किस ताप तक नाप सकता है?
- 7एक सेन्टीग्रेड तथा फैरेनहाइट थर्मामीटर को उबलते पानी में रखा गया । फैरेनहाइट थर्मामीटर में पानी का ताप $140^{\circ}$ तक घटाया गया तो सेन्टीग्रेड स्केल में तापमान है:View Solution
- 8$40$ ग्राम एल्यूमिनियम की ऊष्मीय क्षमता $( S =0.2$ कैलोरी/ग्राम$)$View Solution
- 9$10$ ग्राम बर्फ $0^{\circ} C$ पर एक बर्तन $($जल तुल्यांक $55$ ग्राम$)$ में डाल दी गयी जिसका ताप $40^{\circ} C$ है। माना कि बाहर से कोई ऊष्मा अन्दर नहीं गयी तो बर्तन में पानी का तापमान होगा $( L =80$ कैलोरी/ग्राम $)$ :View Solution
- 10View Solutionकिसी गैस को समतापीय रूप से उसके आधे आयतन तक संपीडित किया जाता है। इसी गैस को पृथक रूप से रुद्धोप्म प्रक्रिया द्वारा उसके आधे आयतन तक संपीडित किया जाता है तब :
- 11कोई रेफ्रिजरेटर $4^{\circ} C$ और $30^{\circ} C$ के बीच कार्य करता है। प्रशीतन किए जाने वाले स्थान का ताप नियत रखने के लिए $600$ कैलोरी ऊप्मा का प्रति सेकण्ड बाहर निकालना आवश्यक होता है। इसके लिए आवश्यक शक्ति चाहिए :View Solution
- 12View Solutionकिसी आदर्श गैस को गई प्रक्रमों द्वारा इसके प्रारंभिक आयतन के आधे आयतन तक संपीडित किया जाता है। किस प्रक्रम में गैस पर अधिकतम कार्य करना होगा?
- 13किसी प्रशांतक $($रेफ्रिजरेटर$)$ का निप्पादन गुणांक $5$ है। यदि फ्रीजर का भीतरी ताप $-20^{\circ} C$ है, तो प्रशीतक के बाहर चारो ओर जहाँ यह ताप बाहर फेंकता है का तापमान होगा :View Solution
- 14किसी एक परमाण्विक गैस का दाब $p$ और आयतन $V$ है। इसमें पहले समतापीय रूप से $2 V$ आयतन तक और फिर रूद्धोष्म रूप से $16 V$ आयतन तक प्रसार होता है। यदि $\gamma=\frac{5}{3}$ हो तो, गैस का अन्तिम दाब होगाView Solution
- 15कोई ऊष्मागतिक निकाय आरेख में दर्शाये गये अनुसार चक्रिय प्रक्रम $\text{ABCDA}$ पर चलता है। निकाय द्वारा इस चक्र में किया गया कार्य होगाView Solution
- 16किसी रूद्धोष्म प्रक्रम में एक गैस का दाब उसके ताप के घन (क्यूब) के समानुपाती पाया जाता है, तो इस गैस के $\frac{C_p}{C_v}$ का अनुपात है:View Solution
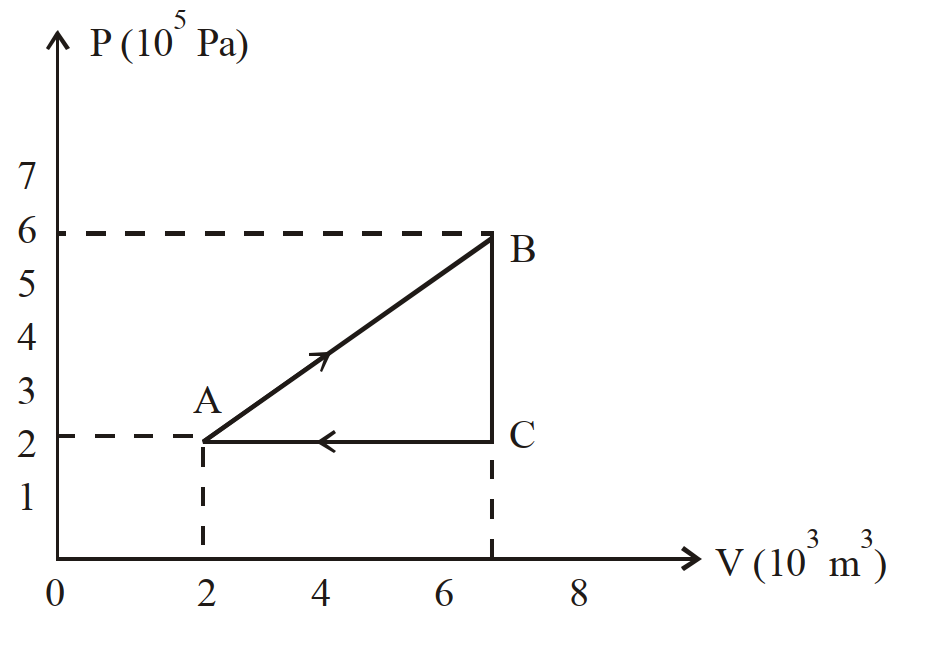
- 17एक गैस को चित्र $($आरेख$)$ में दर्शाये गये अनुसार $A \rightarrow B \rightarrow C \rightarrow A$, चक्र से गुजारा जाता है। तो, गैस द्वारा किया गया नेट कार्य है:View Solution
- 18दिखाये गये P-V आरेख के अनुसार आदर्श गैस को तीन विभिन्न प्रक्रमों द्वारा स्थिति $A$ से $B$ तक ले जाया जाता है।View Solution
यदि इन तीन प्रक्रमों में, अवशोषित ऊष्मा क्रमशः $Q_1$, $Q_2$ तथा $Q_3$ और आन्तरिक ऊर्जा में परिवर्तन $\Delta U_1$, $\Delta U_2$, तथा $\Delta U_3$ हो तो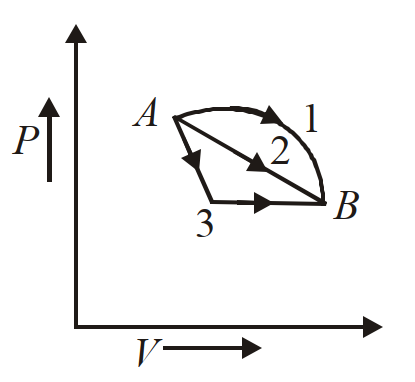
- 19एक मोल आदर्श गैस, प्रारंभिक अवस्था $A$ से अन्तिम अवस्था $B$ को निम्नलिखित दो प्रक्रमों से होकर जाती है। पहले इसके आयतन का $V$ से $3 V$ तक समतापीय रूप से प्रसार होता है। फिर, स्थिर दाब पर इसका आयतन $3 V$ से $V$ तक कम किया जाता है तो, इन दो प्रकमों को निरूपित करने के लिए सही $P-V$ आरेख है:View Solution
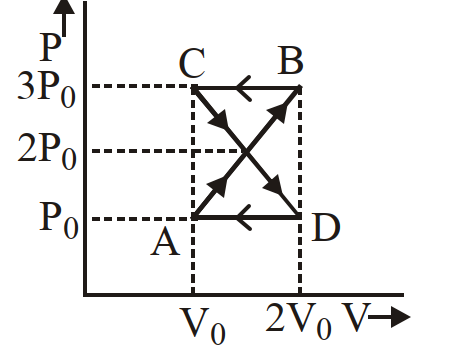
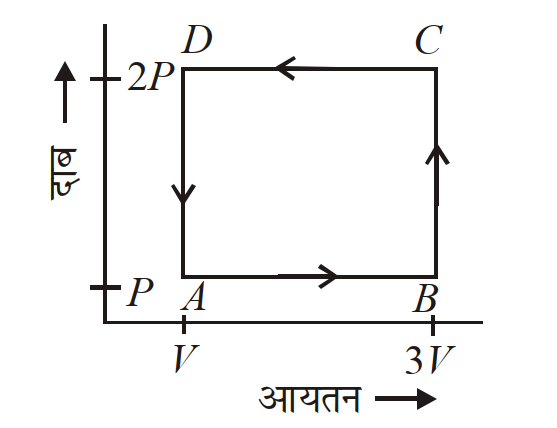
- 20किसी उष्मागतिक निकाय को आरेख में दिखाये गये अनुसार $ABCD$ चक्र से गुजारा जाता है। इस चक्र में गैस द्वारा निकाली गई ऊष्मा का मान होगा :View Solution
- 21एक द्विपरमाणुक गैस $(\gamma=1.4)$ के किसी द्रव्यमान का दाब 2 वायुमंडलीय दाब के बराबर है। इसको रूद्धोष्म अवस्था में इतना संपीडित किया जाता है कि उसका ताप $27^{\circ} C$ से $927^{\circ} C$ हो जाता है। अंतिम अवस्था में गैस का दाब है :View Solution
- 22समतापीय प्रसार में एक परिबद्ध आदर्श गैस अपने वातावरण के विरूद्ध $-150 J$ कार्य करती है, इससे यह निष्कर्ष निकलता है कि:View Solution
- 23जब $0^{\circ} C$ की $1 kg$ बर्फ $0^{\circ} C$ के जल में परिवर्तित होती है तो इसकी एन्ट्रापी में परिणामी परिवर्तन होगा (यदि बर्फ की गुप्त ऊष्मा $80 cal /{ }^{\circ} C$ हो ):View Solution
- 24किसी एक परमाणुक गैस का दाब $P_1$ और आयतन $V_1$ है। इसको रूद्धोष्म रूप से प्रारंभिक आयतन के $1 / 8$ तक संपीडित किया जाता है, गैस का अंतिम दाब कितना होगाView Solution
- 25यदि किसी ताप गतिक प्रक्रम में, निकाय की आन्तरिक ऊर्जा में वृद्धि $\Delta U$ और उसके द्वारा किया गया कार्य $\Delta W$ हो तो, निम्नलिखित में से कौन सा सत्य (सही) है?View Solution
- 26View Solutionऊष्मागतिकी प्रक्रमों के सम्बन्ध में निम्न कथनों में से कौन सा सत्य नहीं है:-
- 27जिस तन्त्र ने $2 kcal$ ऊष्मा का अवशोषण किया हो और $500 J$ कार्य किया हो तो उसमें आन्तरिक ऊर्जा परिवर्तनका मान होगा :-View Solution
- 28एक चक्रीय प्रक्रम में $Q , E$ और $W$ क्रमानुसार, डाली गई ऊष्मा, आन्तरिक ऊर्जा में परिवर्तन और किया गया कार्य दर्शाते हों, तो होगा :View Solution
- 29एक इंजन $1 / 6$ की दक्षता रखता है। जब इसके गर्त के तापमान को $62^{\circ} C$ से कम कर दिया जाता है, तो इसकी दक्षता दोगुनी हो जाती है। स्त्रोत का तापमान होगा $-$View Solution
- 30एक कार्नो इंजन के गर्त $($सिंक$)$ का ताप $300 K$ है और इसकी दक्षता $40 \%$ है। स्रोत ताप को कितना बढ़ाया जाए कि इंजन की दक्षता इसकी पहली दक्षता से $50 \%$ अधिक हो जाए?View Solution
- 31एक आदर्श गैस के लिए स्थिर दाब अवस्था में मोलर विशिष्ट ऊष्मा का मान $(7/2) \ R$ है। इसके लिए स्थिर दाब और स्थिर आयतन अवस्थाओं में विशिष्ट ऊष्माओं का अनुपात होगाView Solution
- 32View Solutionनिम्न में से कौन-सी उत्क्रमणीय प्रक्रिया है?
- 33एक आदर्श गैस ऊष्मा इंजन कार्नो चक्र में $227^{\circ} C$ तथा $127^{\circ} C$ के बीच कार्यरत है। यह उच्च ताप पर $6 \times 10^4$ कैलोरी ऊष्मा अवशोषित करता है। कार्य में परिवर्तित ऊष्मा का मान हैView Solution
- 34प्रारम्भिक ताप $TK$ पर आदर्श गैस का एक मोल रुद्धोष्मीय रूप से $6 R$ जूल कार्य करता है। यदि नियत दाब तथा आयतन पर गैस की विशिष्ट ऊष्माओं का अनुपात $5 / 3$ है, तो गैस का अन्तिम ताप होगा :View Solution
- 35एक आदर्श गैस ऊष्मीय इंजन $227^{\circ} C$ व $127^{\circ} C$ कार्नो चक्र में कार्य करता है। यह उच्च ताप पर $6$ किलो कैलोरी ऊष्मा का अवशोषण करता है। ऊष्मा की कितनी मात्रा $($किलो कैलोरी में$)$ कार्य में परिवर्तित होती हैView Solution
- 36एक कार्नोट इंजन की दक्षता $50 \%$ है, यदि सिंक का ताप $500 K$ है। यदि स्रोत का ताप समान है तो दक्षता $60 \%$ करने के लिए सिंक का ताप होगा: $-$View Solution
- 37एक इंजन के स्रोत्र तथा सिंक का तापमान $127^{\circ} C$ तथा $27^{\circ} C$ है। यह $26 \%$ दक्षता बताता है तो:View Solution
- 38एक उत्क्रमणीय इंजन ली गयी ऊष्मा का $1 / 6$ कार्य में बदलता है । यदि सिंक का तापतान $60^{\circ} C$ कम कर दिया जाए तो दक्षता दोगुनी हो जाती है । तो स्रोत्र तथा सिंक का तापमान होगा :View Solution
- 39एक आदर्श गैस को $27^{\circ} C$ से रुद्धोष्म प्रक्रम में दबाया गया तो उसका आयतन प्रारंभिक आयतन का $8 / 27$ हो गया । इसके तापमान में वृद्धि होगी $( r =5 / 3)$View Solution
- 40नियत दाब तथा नियत आयतन पर विश्ष्ट ऊष्मा का अनुपात $r$ है। यदि गैस का आयतन स्थिर दाब $P$ पर $V$ से $2 V$ कर दिया जाए तो गैस की आन्तरिक ऊर्जा में वृद्धि होगी :View Solution
- 41एक ऊष्मागतिकी प्रक्रम के लिए $\Delta U =$ आंतरिक ऊर्जा में वृद्धि को दर्शाता हो तथा $W =$ किया कार्य हो तो कौन सा कथन सत्य है?View Solution
- 42एक गैस को आयतन $V _1$ से $V _2$ तक प्रसारित किया गया किस प्रक्रम में किया गया कार्य अधिकतम होगा:View Solution
- 43एक कार्नो इंजन $100^{\circ} C$ तथा $-23^{\circ} C$ पर कार्य करता है। इसकी दक्षता होगी :View Solution
- 44एक द्विआण्विक गैस को $18^{\circ} C$ पर रुद्धोष्म परिवर्तन के अनुसार दबाया गया जिससे इसका आयतन प्रारम्भिक आयतन का $1 / 8$ हो गया। अन्तिम ताप होगा:View Solution
- 45View Solutionएक आदर्श गैस में रुद्धोष्म परिवर्तन होता है । इसके दाब तथा ताप के बीच संबंध होगा:
- 46एक आदर्श कार्नो इंजन की दक्षता $40 \%$ है जबकि वह $500 K$ से ऊष्मा प्राप्त करता है । यदि दक्षता $50 \%$ करनी हो तो कितने ताप पर ऊष्मा प्राप्त करेगा:View Solution
- 47एक गैसीय निकाय को $110 J$ ऊष्मा दी गयी जिसकी आन्तरिक ऊर्जा $40 J$ है । इसमे किया गया कार्य होगा:View Solution
- 48एक आदर्श गैस $A$ तथा वास्तविक गैस $B$ के आयतन $V$ से $2 V$ तक समतापीय स्थिति में बढ़ा दिये गये। इसकी आंतरिक ऊर्जा में वृद्धि:View Solution
- 49View Solutionनिम्न में से कौन सा ऊष्मागतिकीय फलन नहीं है?
- 50किसी गैस के लिए $R / C _{ v }=0.67$, इस गैस में अणुस्थिति हैView Solution
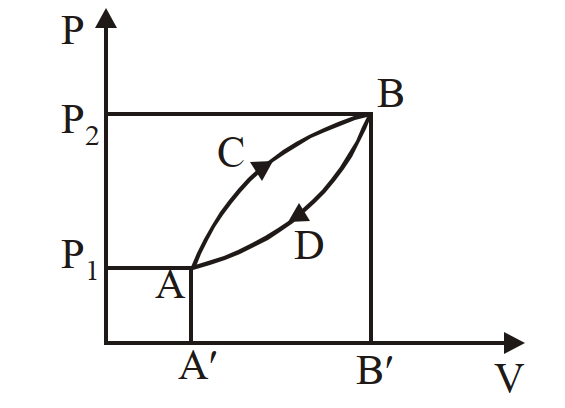
- 51एक ऊष्मागतिकी प्रक्रम (चित्र देखें) में गैस को $A$ से $B$ तक $ACB$ द्वारा फिर वापिस $A$ तक $BDA$ द्वारा लाया गया है। पूरे प्रक्रम में किया गया कार्य किस क्षेत्रफल के बराबर होगा?View Solution
- 52यदि हाइड्रोजन के लिए $C _{ p }- C _{ v }= a$; आक्सीजन के लिए $C _{ p }- C _{ v }= b$, तो $a$ व $b$ के बीच संबंध हैView Solution
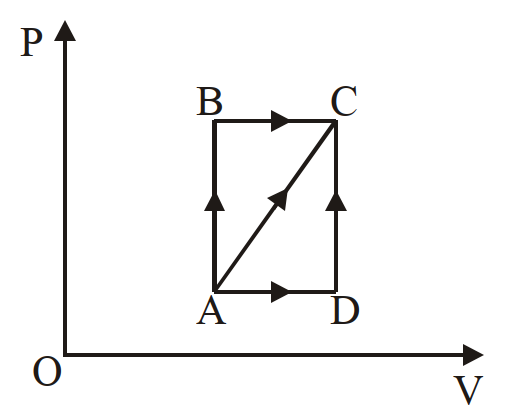
- 53चित्र में उष्मागतिकी प्रक्रम दिखाया गया है । कुछ बिन्दुओं पर दाब व आयतन निम्न प्रकार है $P _{ A }=3 \times 10^4 Pa , V _{ A }$ $=2 \times 10^{-3}$, मी $^3 P _{ B }=8 \times 10^4 Pa , V _{ B }=5 \times 10^{-3}$ मी $^3$. प्रक्रम $AB$ में $600 J$ ऊष्मा दी गयी तथा $BC$ में $200 J$ ऊष्मा दी गयी। $AC$ प्रक्रम में आन्तरिक ऊर्जा में परिवर्तन होगा:View Solution
- 54$27^{\circ} C$ पर किसी गैस का दाब अचानक प्रारम्भिक दाब का $1 / 8$ कर दिया गया। अन्तिम ताप बताइये $(r=5 / 3)$View Solution
- 55View Solutionऊष्मागतिकी का प्रथम नियम किसके संरक्षण पर आधारित है।
- 56ताप $27^{\circ} C$ और दाब $1.0 \times 10^5 Nm ^{-2}$ पर किसी दिए गए द्रव्यमान की गैस के अणुओं का वर्ग माध्य मूल (\text{r.m.s}) वेग $200 \ ms ^{-1}$ है। जब इस गैस के ताप और दाब क्रमशः $127^{\circ} C$ और $0.05 \times 10^5 \ Nm ^{-2}$ है, तो $ms ^{-1}$ में इस गैस के अणुओं का वर्ग माध्य मूल वेग है :View Solution
- 57एक समान तापमान पर दो पात्रों में से एक में आदर्श गैस $A$ तथा दूसरे में आदर्श गैस $B$ भरी है। गैस $A$ का दाब गैस $B$ के दाब का दो गुना है। इन दशाओं के अन्तर्गत गैस $A$ का घनत्व गैस $B$ के घनत्व से $1.5$ गुना पाया जाता है, तो $A$ तथा $B$ के अणुभारों का अनुपात होगा:View Solution
- 58सामान्य ताप तथा दाब पर किसी गैस के $4.0 g$ द्रव्यमान का आयतन $22.4$ लिटर है। स्थिर आयतन पर इसकी विशिप्ट ऊप्मा धारिता $5.0 JK ^{-1} \text{mol} ^{-1}$ है। यदि इस गैस में सामान्य ताप व दाब पर ध्वनि का वेग $952 \ ms ^{-1}$ है तो इस गैस की रिथर दाब विशिप्ट ऊप्मा धारिता है (गैस नियतांक $R =8.3 JK ^{-1} \text{mol} ^{-1} )$View Solution
- 59यदि किसी गैस के अणुओं की त्रिज्या $r$ हो तो, उनका माध्य-मुक्त-पथ व्युत्क्रमानुपाती होता हैView Solution
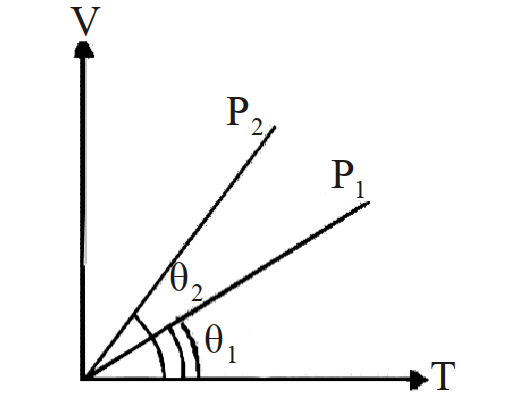
- 60दर्शाये गये $( V - T )$ आरोख में, दाब $P _1$ तथा $P _2$ के बीच क्या संबंध है ?View Solution
- 61मानक ताप व दाब पर $1 g$ हीलियम का ताप $T_1$ कैल्विन से $T _2$ कैल्विन तक बढ़ाने के लिये आवश्यक ऊष्मीय ऊर्जा का मान है:View Solution
- 62यदि किसी आदर्श गैस का अणुभार $M$ है। $C _p$ और $C _v$ इसकी विशिष्ट ऊष्मा (प्रति इकाई द्रव्यमान) है। तो-View Solution
- 63$10^{\circ} C$ पर एक आदर्श गैस के नियत द्रव्यमान के गैस के घनत्व का दाब से विभाजन का फल $x$ हो तो $110^{\circ} C$ पर इस अनुपात का मान होगा :View Solution
- 64$30^{\circ}$ वायुमंडलीय दाब तथा $27^{\circ} C$ पर एक गैस को $1$ वायुमंडलीय दाब तक प्रसारित किया गया । यदि आयतन प्रारम्भिक आयतन का $10$ गुना हो तो अन्तिम ताप होगा।View Solution
- 65यदि परफैक्ट गैस की विशिष्ट ऊष्माओं का अनुपात $r$ है तो अणु की स्वतंत्रता डिग्री का मानःView Solution
- 668 ग्राम $O _2$ के लिए गैस समीकरण होगीView Solution
- 67$C _{ s }$ ध्वनि का हवा वेग है तथा $C$ वर्ग माध्य मूल मान है तो:View Solution
- 68एक गैस का तापमान $27^{\circ} C$ से बढाकर $927^{\circ} C$ कर दिया गया। तो वर्ग माध्य मूल वेग का मान:View Solution
- 69View Solutionद्विआण्विक गैसों में स्थानांतरीय स्वतंत्रता की कोटि होंगी
- 70एक गैस के लिए दाब $( P )$ तथा ऊर्जा $( E )$ के बीच संबंध है:View Solution
- 71नियत दाब पर एक एक परमाण्विक आइडियल गैस के एक मोल का ताप $10 K$ बढ़ाने के लिए $207 J$ ऊष्मा की आवश्यकता है। इसी गैस के नियत आयतन पर $10 K$ तापमान वृद्वि के लिए आवश्यक ऊष्मा है $( R = 8.3$ जूल/मोल $K )$View Solution
- 72तीन बर्तनों में तीन अलग-अलग गैसें समान आयतन की भर दी गयी। अणुओं का द्रव्यमान क्रमशः $m _1, m _2, m _3$. तथा अणुओं की संख्या $N _1, N _2, N _3$ है। बर्तनों में गैसों का दाब क्रमश: $P _1, P _2, P _3$ है। तीनों गैसों को मिलाकर एक बर्तन में डाल दिया गया तो गैसों का दाब $P$ होगा:View Solution
- 73किसी गैस के लिए विशिष्ट ऊष्माओं का अनुपात $r=1.5$ है। इस गैस के लिए :View Solution
- 74View Solutionगैंसों की गतिकी सिद्धांत के अनुसार परम शून्य ताप पर
- 75View Solutionनियत आयतन पर ताप बढ़ता है क्योंकि
- 76एक बहुआण्विक गैस में स्वतंत्रता-डिग्री $n$ है तो प्रति परमाणु माध्य ऊर्जा होगी:View Solution
- 77दो बर्तनों $A$ तथा $B$ में थोड़ा पानी भरकर बंद कर दिया गया । $A$ का आयतन $B$ से दोगुना है तथा $A$ में पानी का आयतन $B$ से आधा है । यदि दोनों का तापमान समान हो तो दोनों में वाष्प के दाब का अनुपात होगा:View Solution
- 78सरल आवर्त गति करते हुए किसी कण का अधिकतम त्वरण $\alpha$ तथा अधिकतम वेग $\beta$ है तो, इसके कम्पन का आवर्तकाल होगा :View Solution
- 79किसी पिण्ड $($वस्तु$)$ के चिकेने क्षैतिज पृष्ठ $($सतह$)$ पर दोलनों के समीकरण को $X=A \cos (\omega t)$ द्वारा निरूपित किया जाता है, जहां $X=t$ समय पर विस्थापन $\omega=$ दोलनों की आवृत्ति तो, $t$ के साथ $a$ के विचलन $($परिवर्तन$)$ को कौन $-$ सा ग्राफ $($आलेख$)$ सही रूप में दर्शाता है ?View Solution
- 80किसी सरल आर्वत तरंग का समीकरण $ y=3 \sin \frac{\pi}{2}(50 t-x) $ जहाँ $x$ तथा $y$ मीटर में और $t$ सेकंड में है तो, अधिकतम कण $-$ वेग तथा तरंग वेग का अनुपात होगा :View Solution
- 81View Solutionकिसी दोलित्र पर अवमन्दन-बल वेग के समानुपाती होता है तो, समानुपाती नियतांक का मात्रक है :
- 82दो कण, एक दूसरे के निकट स्थित, दो समान्तर सरल रेखाओं के अनुदिश, समान आवृति और आयाम से दोलन कर रहे हैं। जब उनका विस्थापन उनके आयाम का आधा $(1 / 2)$ होता है तो वे एक दूसरे से विपरीत दिशा में गति कर रहे होते हैं। दोनों कणों की माध्य स्थिति, उनके मार्गों की लम्बवत् एक सरल रेखा पर स्थित है। तो कलान्तर है :View Solution
- 83किसी कण को प्रदर्शित करने वाले निम्नलिखित फलनों में कौन से फलन सरल आवर्त गति को निरूपित करते है? (A) $y=\sin \omega t-\cos \omega t$ (B) $y=\sin ^3 \omega t$ (C) $y=5 \cos \left(\frac{3 \pi}{4}-3 \omega t\right)$ (D) $y =1+\omega t +\omega^2 t ^2$View Solution
- 84दो तरंगों को क्रमशः $y _1= a \sin (\omega t + kx +0.57) m$ तथा $y _2= a \cos (\omega t + kx ) m,$ से निरूपित किया जाता है, जहाँ $x$ मीटर में और $t$ सैकण्ड में है, तो दोनों तरंगों के बीच कलान्तर है:View Solution
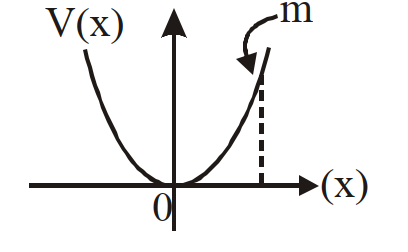
- 85एक कण का द्रव्यमान $m$ है। इसे विराम अवस्था से मोचित किया गया है और यह आरेख मे दिखाये गये अनुसार एक परवलीय मार्ग पर चलता है। यह मानते हुए कि कण का मूल स्थिति से विस्थापन कम है, कौन से ग्राफ कण की स्थिति को समय के फलन के रूप में सही दर्शाता है?View Solution
- 86कोई कण $x-y$ समतल में $x= a \sin \omega t$ तथा $y=a \cos \omega t$ के अनुसार गति करता है। कण का पथ होगाView Solution
- 87किसी कण का, $x$ अक्ष के अनुदिश विस्थापन $x = a \ \sin ^2 \omega t$ से दिया जाता है। इस कण की गति हैView Solution
- 88किसी नगण्य द्रव्यमान के स्प्रिंग से लटकाये गये $M$ द्रव्यमान का दोलनकाल $T$ है। यदि इसके साथ ही एक अन्य $M$ द्रव्यमान लटका दिया जाय तो दोलनकाल हो जायेगाView Solution
- 89निम्न समीकरणों में से कौन सी सरल आवर्ती चाल की सूचक है:- (जबकि $k , k _0, k _1$ और $a$ सभी, धनमानी हैं।)View Solution
- 90एक सरल लोलक $x=0$ के परित: सरल आवर्ती चाल से चल रहा है जिसका आयाम $a$ और समय अन्तराल $T$ है। $x =\frac{ a }{2}$ पर लोलक की चाल होगी :-View Solution
- 91दो सरल आवर्त गतियाँ जिनकी कोणीय आवृतियाँ $100$ और $1000$ रैडियन प्रति सेकेण्ड हैं, समान विस्थापन आयाम रखती हैं। उनके अधिकतम त्वरणों का अनुपात होगा :View Solution
- 92एक बिन्दु सरल आवर्त दोलन करता है जिसका आवर्तकाल $T$ और चलन का समीकरण $x = a \sin (\omega t +\pi / 6)$ है। आवर्तकाल के किस अंश के पश्चात् बिन्दु का वेग उसके अधिकतम वेग का आधा होगा ?View Solution
- 93एक कण सरल आवर्ती गति में है। इसके तात्क्षणिक वेग और त्वरण का कलान्तर होगा $-$View Solution
- 94एक कण आयाम $a$ के साथ सरल आवर्ती दोलन करता है। इसका दोलनकाल $T$ है। इस कण को अपनी साम्य अवस्था से आयाम की आधी दूरी चलने में लगने वाला कम से कम समय होगा $-$View Solution
- 95एक कण सरल आवर्ती गति में है। इसकी गतिज ऊर्जा $K _0 \cos ^2 \omega t$ है। इसकी स्थितिज ऊर्जा और सम्पूर्ण ऊर्जा के क्रमानुसार अधिकतम मान होंगे $-$View Solution
- 96एक ऊर्ध्व दिशा की कमानी को धरातल पर चित्र के अनुसार स्थायी किया गया है तथा इसके ऊपरी सिरे के पलड़े पर $2.0$ किग्रा द्रव्यमान की वस्तु रखी है। कमानी और पलड़े के भार नगण्य हैं। थोड़ा दबाकर छोड़ देने पर द्रव्यमान सरल आवर्ती गति करता है। कमानी का बल नियतांक 200 न्यूटन/मी है। आवर्त गति का न्यूनतम आयाम कितना होना चाहिए, जिससे ऊपर रखी वस्तु पलड़े से अलग हो जाये?( मान लो $g =10$ मी $/$ से $^2$ )View Solution

- 97जब एक लम्बे स्प्रिंग को $2$ सेमी खींचा जाता है तो इसमें संचित स्थितिज ऊर्जा $U$ होती है। यदि इसे $8$ सेमी खींचा जाए तो इसमें संचित स्थितिज ऊर्जा होगी:View Solution
- 98$5$ सेमी आयाम की सरल आवर्त गति करते एक कण की अधिकतम चाल $31.4$ सेमी./से है। इसके कम्पन की आवृत्ति हैView Solution
- 99सरल आवर्त गति करते एक कण की चाल $v$ तथा त्वरण $a$ के लिए, तिम्नलिखित में से कौन $-$ सा कथन सत्य है?View Solution
- 100बल नियतांक $k _1$ व $k _2$ वाली दो स्प्रिंगो को श्रेणी क्रम में जोड़ा गया है। संयोग का प्रभावी बल नियतांक है:View Solution