Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1View Solutionएक कार शून्य से चलकर 20 सेकंड में 44 किमी/घंटे का वेग प्राप्त कर लेती है। इसने कितनी दूरी तय की?
- 2एक कण का विस्थापन समय के साथ $s=a t^2-b t^3$ से दिया जाता है। किसी क्षण इसका त्वरण होगा-View Solution
- 3एक बॉल ऊध्र्वाधरतः ऊपर की ओर 40 मी/सेकंड से फेंक दी गयी। 2 सेकंड बाद बॉल का वेग होगा: $( g =10$ मी/सेकंड 2 )View Solution
- 4पृथ्वी तल से 5 मीटर ऊंचाई पर स्थित एक टोटी से पानी की बूंदें बराबर समयान्तर पर गिरती है। पानी की तीसरी बूंद टोटी से तब निकलती है जब पहली बूंद पृथ्वी तल को छूती है। इस क्षण दूसरी बूंद पृथ्वी तल से कितनी ऊंचाई पर है? $( g =10$ मी/सेकंड 2$)$View Solution
- 5View Solutionएक पिण्ड पृथ्वी तल से ऊध्र्वाधरतः ऊपर की तरफ फेंका गया। यह उच्चतम ऊंचाई 20 मी. तक 5 सेकंड में पहुंचता है। यह वापस पृथ्वी तल पर कितने समय में आएगा।
- 6तीन भिन्न पिण्ड जिनके द्रव्यमान $m _1, m _2, m _3$ है को एक साथ एक ऊंचाई से छोड़ तीन अलग घर्षणतहित पथों से दिया गया। पृथ्वीतल पर पहुंचने पर इनके वेगों का अनुपात होगा-View Solution
- 7एक पत्थर शून्य वेग से एक टॉवर के शिखर से छोड़ने पर यह पृथ्वीतल पर 5 सेकंड में पहुंचता है। खम्बे की ऊंचाई $\left( g =10\right.$ मी/सेकंड $\left.{ }^2\right)$View Solution
- 8View Solutionचित्र में विस्थापन-समय ग्राफ दिखाया गया है। कण की क्षणिक वेग किस बिन्दु पर ऋणात्मक होगी?
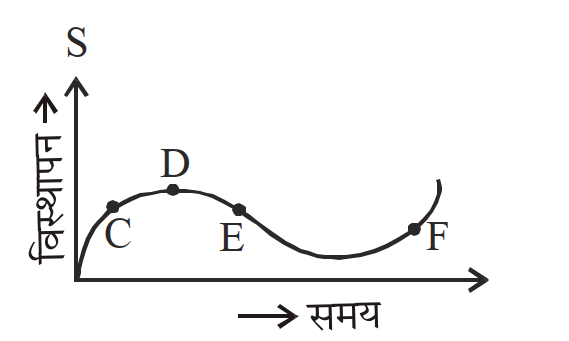
- 9एक कण सरल रेखा में चलता है। इसका $t$ समय के साथ विस्थापन $s=t^3-6 t^2+3 t+4$ मी से दिया गया है। त्वरण शून्य होने पर वेग का मान होगा-View Solution
- 10एक कार विरामावस्था से चलकर कुछ समय बाद $\alpha$ त्वरण प्राप्त कर लेती है तथा फिर $\beta$ मंदन से चलकर रूक जाती है। यदि कुल लिया गया समय $t$ हो तो कार का अधिकतम वेग होगा-View Solution
- 11View Solutionएक वस्तु विरामावस्था से चलती है। इसके द्वारा चौथे सेकंड तथा तीसरे सेकंड में चली गयी दूरियों का अनुपात होगा।
- 12View Solutionदिये गये ग्राफ में कौन-सा एक विमीय गति प्रदर्शित नहीं करता?
- 13एक कार 200 मीटर की दूरी तय करती है। यात्रा का पहला आधा भाग वह 40 किमी/घंटा वेग से तथा दूसरा आधा भाग $v$ वेग से चलती है। यदि औसत वेग 48 किमी/घंटा है तो $v$ का मान है-View Solution
- 14एक पिण्ड को एक टॉवर के शिखर से छोड़ा गया। यह यात्रा के अंतिम दो सेकण्डों में 40 मी. चलता है। तो टॉवर की ऊंचाई होगी $\left( g =10\right.$ मी/सेकंड $\left.{ }^2\right)$View Solution
- 15View Solutionएक बस किसी दूरी का एक तिहाई 10 किमी/घंटा वेग से, दूसरा तिहाई भाग 40 किमी/घंटा वेग से तथा तीसरा तिहाई भाग 60 किमी/घंटा वेग से चलती है। बस का औसत वेग होगा-
- 16View Solutionदो स्थानों के बीच एक कार चलती है। यात्रा का आधा भाग वह 40 किमी/घंटा से तथा दूसरा भाग 60 किमी/घंटा से चलती है। कार का औसत वेग है-
- 17View Solutionविराम की अवस्था से गिरती हुई दो चीजों द्वारा यात्रा के चौथे सेकंड तथा पांचवें सेकंड में चली गयी दूरियों का अनुपात है-
- 18View Solutionएक ट्रेन की लम्बाई 150 मी. है। यह उत्तर दिशा में 10 मी./सेकंड के वेग से चलती है। एक तोता 5 मी./सेकंड से दक्षिण दिशा में रेलमार्ग के समान्तर उड़ता है। कितने समय में तोता ट्रेन को पार कर जाएगा।
- 19एक कार एक सीधी सड़क पर एक समान त्वरण से चलती है। यह दो बिन्दुओं $P$ तथा $Q$ से 30 किमी/घंटा तथा 40 किमी/घंटा से गुजरती है। P तथा Q कुछ दुरी पर है। तो $P$ तथा $Q$ के मध्य बिन्दु पर कार का वेग है-View Solution
- 20View Solutionयदि दो सदिशों के योग का परिमाण उन दो सदिशों के अन्तर के परिमाण के बराबर है, तो इन सदिशों के बीच का कोण है:
- 21समय के फलन के रूप में किसी कण का स्तिथि सदिश $\overrightarrow{ R }$ दिया गया है: $ \vec{R}=4 \sin (2 \pi t) \hat{i}+4 \cos (2 \pi t) \hat{j} $जहाँ $R$ मीटर में तथा $t$ सेकण्ड में है और $\hat{ i }$ तथा $\hat{ j }$ क्रमश: $X$-तथा $y$-दिशाओं के अनुदिश एकांक सदिश हैं। इस कण की गति के लिये निम्नांकित में से कौनसा कथन सही नहीं है?View Solution
- 22यदि सदिश $\overrightarrow{ A }=\cos \omega t \hat{i}+\sin \omega \hat{ j }$ तथा सदिश $\overrightarrow{ B }=\cos \frac{\omega t }{2} \hat{ i }+\sin \frac{\omega t }{2} \hat{ j }$ समय के फलन है, तो $t$ का मान क्या होगा जिस पर ये सदिश परस्पर लंबकोणि होगी?View Solution
- 23एक कण इस प्रकार गति करता है कि इसके स्थिति निर्देशांक $(x, y)$ निम्न प्रकार हैं (2मी, 3 मी) समय $t=0$ पर (6मी, 7 मी) समय $t=2$ सेकण्ड पर (13मी, 14 मी) समय $t=5$ सेकेण्ड पर तो, $t =0$ से $t =5$ सेकण्ड तक, औसत वेग सदिश $\left(\overrightarrow{ V }_{ av }\right)$ होगाView Solution
- 24एक प्रक्षेप्य को पृथ्वी की सतह से 5 मी/से के वेग से क्षैतिज दिशा से $\theta$ कोण पर छोड़ा जाता है। किसी अन्य ग्रह से 3 मी/से के वेग तथा इसी कोण $(\theta)$ पर छोड़े गये एक प्रक्षेप्य का प्रक्षेप पथ, पृथ्वी से छोड़े गये प्रक्षेप्य के प्रक्षेप पथ के सर्वसम (सर्वथा समान) है। यदि पृथ्वी पर मी $/ से ^2$ में होगा।View Solution
- 25किसी प्रक्षेप्य का प्रारंभिक बिन्दु $A$ पर वेग $(2 \hat{i}+3 \hat{j})$ $m / s$. है, तो इसका बिन्दु $B$ पर वेग $( m / s$ में) होगा:View Solution
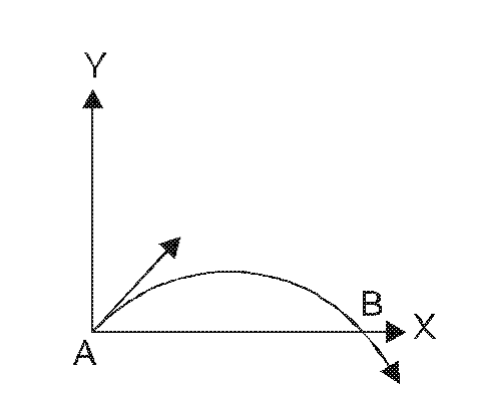
- 26View Solutionकिसी प्रक्षेप्य की अधिकतम् ऊँचाई तथा क्षैतिज परास आपस में बराबर है तो, प्रक्षेप्य का प्रक्षेपण कोण है :
- 27किसी कण का प्रारंभिक वेग $(2 \vec{i}+3 \vec{j})$ तथा त्वरण $(0.3 \vec{i}+0.2 \vec{j})$ है। 10 सेकण्ड बाद कण के वेग का मान होगा :View Solution
- 28एक प्रक्षेप्य को क्षैतिज से $45^{\circ}$ के कोण पर प्रक्षेपित किया गया है, तो प्रक्षेप बिन्दु से देखने से, प्रक्षेप्य के उच्चतम बिन्दु पर उसका उन्नयन कोण होगा:View Solution
- 29एक प्रक्षेपास्त्र को अधिकतम परास के लिए प्रक्षेपित किया गया है। इसका प्रारम्भिक वेग $20 m / s$ है। यदि $g =10 m / s ^2$ हो तो प्रक्षेपास्त्र का परास होगा:View Solution
- 30एक वस्तु $30 m / s$ वेग से पूर्व की ओर गति कर रही है। 10 सैकण्ड के पश्चात् इसका वेग उत्तर की ओर $40 m / s$ हो जाता है तो वस्तु का औसत त्वरण है :View Solution
- 31View Solutionअधिकतम ऊँचाई पर किसी प्रक्षेप्य की चाल उसकी प्रारंभिक चाल की आधी है। तो उसके प्रक्षेपण का कोण होगा
- 32$\vec{a}$ से $\vec{f}$ तक छः सदिशों के परिमाणों और दिशाओं को, दिये गये चित्र (आरेख)में प्रदर्शित किया गया है। निम्नलिखित में से कौन सा कथन इनके लिये सत्य (सही) है?View Solution
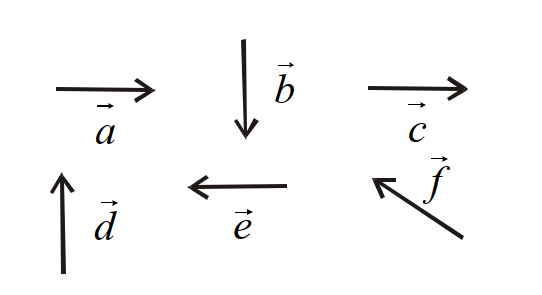
- 33किसी कण का प्रारंभिक वेग $(3 \hat{i}+4 \hat{j})$ तथा त्वरण $(0.4 \hat{i}+0.3 \hat{j})$ है। 10 सेकेण्ड के पश्चात् कण की चाल होगी-View Solution
- 34यदि कोई कण $x=(t+5)^{-1}$ के अनुसार गति करता है, जहाँ $x$ दूरी तथा $t$ समय है तो, कण का त्वरण अनुक्रमानुपाति होगाView Solution
- 35View Solution
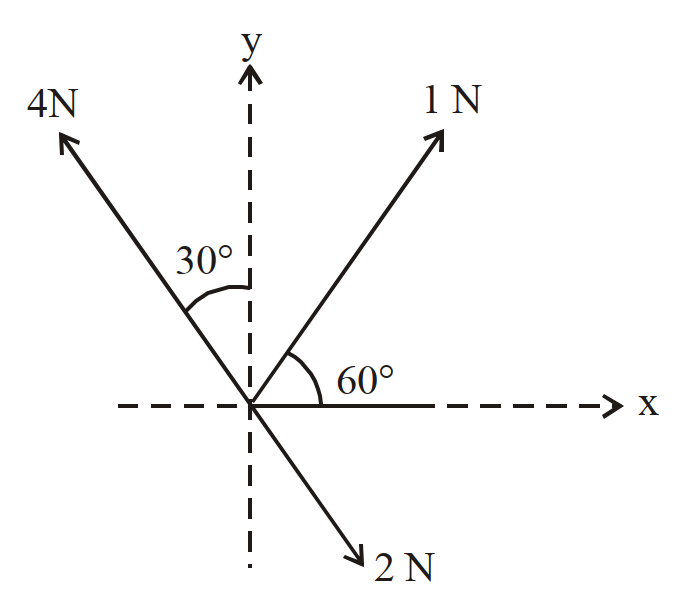
एक वस्तु पर लगे तीन बल इस चित्र में दर्शाए गए हैं। यदि इन बलों का परिणामी बल केवल $y$-दिशा में होना हो तो $X$-अक्ष की दिशा में आवश्यक अतिरिक्त बल का न्यूनतम मान क्या होगा? - 36$m$ द्रव्यमान का एक कण क्षैतिज दिशा से $45^{\circ}$ का कोण बनाते हुए $v$ वेग से प्रक्षेपित किया गया है। कण के समतल जमीन पर उतरने पर उसके संवेग में परिवर्तन का परिमाण होगा :View Solution
- 37$\overrightarrow{ A }$ और $\overrightarrow{ B }$ दो सदिश हैं जिनके बीच का कोण $\theta$ है। यदि $|\overrightarrow{ A } \times \overrightarrow{ B }|=\sqrt{3}(\overrightarrow{ A } \cdot \overrightarrow{ B })$, तो $\theta$ का मान होगा-View Solution
- 38किसी प्रक्षेप्य के लिए प्रक्षेपण कोणों $\left(45^{\circ}-\theta\right)$ और $\left(45^{\circ}\right.$ $+\theta)$ पर, इनके द्वारा तय की गई क्षैतिज परास का अनुपात है:View Solution
- 39एक कार 100 मीटर त्रिज्या वाले वृत्ताकार पथ पर समान चाल से गति कर रही है। यह प्रत्येक चक्कर $62.8$ सेंकड में पूरा करती है। प्रत्येक चक्कर का औसत वेग और औसत चाल क्रमशः है:View Solution
- 40सदिश $\overrightarrow{ A }$ और $\overrightarrow{ B }$. इस प्रकार हैं कि $|\overrightarrow{ A }+\overrightarrow{ B }|=|\overrightarrow{ A }-\overrightarrow{ B }|$ इन दो सदिशों के बीच का कोण है:View Solution
- 41View Solutionएक कण की स्थिर चाल से वृत्तीय गति
- 42यदि एक सदिश $2 \hat{i}+3 \hat{j}+8 \hat{k}$ किसी सदिश $4 \hat{j}-4 \hat{i}+\alpha \hat{k}$ के लम्बवत है तो $\alpha$ का मान है:View Solution
- 43एक मैदान के दो छोरो $A$ और $B$ पर दो लड़के खड़े हैं जहाँ $AB = a$ है। $B$ पर खड़ा हुआ लड़का $AB$ के लम्बवत $v _1$ वेग से दौड़ना शुरू करता है। उसी समय $A$ पर खड़ा हुआ लड़का $v$ वेग से दौड़ना शुरू करता है और दूसरे लड़के को $t$ समय में पकड़ लेता है। $t$ है:View Solution
- 44यदि सदिश $\overrightarrow{ A }$ और $\overrightarrow{ B }$ के बीच का कोण $\theta$ है तो $(\overrightarrow{ B } \times \overrightarrow{ A }) \cdot \overrightarrow{ A }$ का मान है:View Solution
- 45View Solution1 मीटर लम्बी रस्सी के एक सिरे पर पत्थर बाँधकर उसे एक क्षैतिज वृत्त में स्थिर चाल से घुमाया जाता है। यदि पत्थर 44 सेकंड में 22 चक्कर लगाता है तो पत्थर के त्वरण का मान व इसकी दिशा क्या होगी?
- 46यदि $|\overrightarrow{ A } \times \overrightarrow{ B }|=\sqrt{3} \overrightarrow{ A } \cdot \overrightarrow{ B }$ हो तो $|\overrightarrow{ A } \times \overrightarrow{ B }|$ का मान है:View Solution
- 47$\ell$ लम्बाई की रस्सी के एक सिरे पर पत्थर बाँधकर उसके दूसरे सिरे को केंद्र बनाकर उसे ऊर्ध्वाधर वृत्त में घुमाया जाता है। किसी निश्चित समय पर, पत्थर अपनी निम्नतम स्थिति में $u$ वेग से है। जब यह इस स्थिति में पहुँचेगा कि रस्सी क्षैतिज हो तो इसके वेग के परिमाण में परिवर्तन है: $( g$ गुरुत्वीय त्वरण है)View Solution
- 48एक कण $\frac{20}{\pi}$ मीटर त्रिज्या वाले वृत्तीय यहा पर एक समान त्वरण से चलता है। यदि गति शुरू होने के बाद दूसरे चक्कर के खत्म होने पर कण का वेग 80 मी/सेकंड है, तो इसका स्पर्शरेखीय त्वरण है:View Solution
- 49View Solutionदो बलों का सदिश योग उनके अंतर का लम्बवत है। इस स्थिति में
- 50एक 3 किग्रा. का पिण्ड $X Y$ तल में बल $\vec{F}=6 t \hat{i}+4 t \hat{j}$ के प्रभाव में है। मानाt $=0$ पर यह स्थिर है तो $t =3$ सेकंड पर इसका वेग होगाView Solution
- 51View Solution10 मी ऊँच्चे एक मकान से एक पत्थर गिराया जाता है, इसी समय दूसरा समान पत्थर 5 मी/सेकंड से क्षैतिज दिशा में प्रक्षिप्त किया जाता है। कथन सा वचन सत्य है?
- 52यदि दो सदिश $\overrightarrow{ A }=3 \hat{ i }+4 \hat{ j }+5 \hat{ k }$ तथा $\overrightarrow{ B }=3 \hat{ i }+4 \hat{ j }-5 \hat{ k }$ हो तो इनके बीच का कोणView Solution
- 53$M$ तथा $m$ द्रव्यमान केदो कण क्रमशः $R$ तथा $r$ वृत्त के पथ पर घूमते है। यदि उनके आवर्तकाल समान हो, तो उनके रेखीय वेगों का अनुपात होगाView Solution
- 54एक बच्चा झूला झूलता है। झूले की न्यूनतम तथा अधिकतम ऊंचाई (पृथ्वी तल से) $0.75$ मीटर तथा 2 मीटर है। तो झूले का अधिकतम वेग होगाView Solution
- 55एक छोटे गोले को धागे में बांधकर $O$ के सापेक्ष ऊर्ध्वाधर वृत में घुमाया जाता है। यदि उसकी औसत चाल बढ़ायी जाए तो धागा टूटने की स्थिति में आ जाता है। उस समय गोले की स्थिति होगी-View Solution
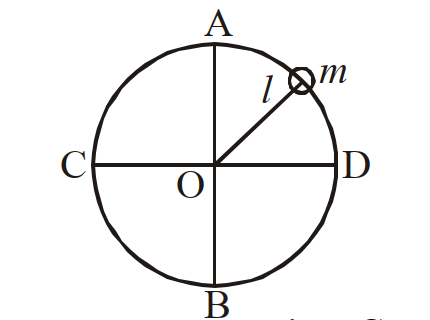
- 56एक कण एक बल $\overrightarrow{ F }=20 \hat{ i }+15 \hat{ j }-5 \hat{ k } N$ के प्रभाव से वेग $6 \hat{i}-4 \hat{j}+3 \hat{k}$ मी/सेकंड से गतिशील है। इसकी क्षमता होगी-View Solution
- 57दो कण किसी बिन्दु से समान वेग से क्षैतिज $60^{\circ}$ तथा $30^{\circ}$ के कोण पर प्रक्षेपित किये जाते है। कौन सा कथन सत्य है?View Solution
- 58View Solutionएक नाव स्थिर पानी में 5 किमी/घंटा से चलती है। नदी की चौड़ाई 1 किमी है। यदि नाव न्यूनतम पथ पर चलकर नदी को 15 मिनट में पार करती है तो नदी के बहाव का वेग होगा:
- 59View Solutionएक धागे से एक पत्थर को बांधकर ऊर्ध्वाधर वृत्त में घुमाया जाता है। न्यूनतम वेग
- 60एक व्यक्ति एक नदी को तैरकर ठीक सामने जाना चाहता है। उसका वेग $0.5$ मी/सेकंड नदी के बहाव से $120^{\circ}$ के कोण पर है। नदी के बहाव का वेग हैView Solution
- 61यदि एक इकाई सदिश $0.5 \hat{i}+8 \hat{j}+c \hat{k}$ से व्यक्त होता है तो $c$ का मान होगा-View Solution
- 62एक $0.4$ किग्रा का द्रव्यमान 2 चक्कर/सेकंड से ऊर्ध्वाधर वृत्त में घुमाया जाता है। वृत्त की त्रिज्या $1.2$ मीटर है तो उच्चतम बिन्दु पर धागे में तनाव होगाView Solution
- 63View Solutionयदि 12 तथा 18 इकाई का परिणामी 24 इकाई है तो इनके बीच का कोण होगा
- 64यदि कोणीय वेग $\vec{\omega}=3 \hat{i}-4 \hat{j}+\hat{k}$ तथा स्थिति सदिश $\overrightarrow{ r }=5 \hat{ i }-6 \hat{ j }+6 \hat{ k }$ हो तो रेखीय वेग होगा:View Solution
- 65View Solutionएक 500 किग्रा की कार 50 मी त्रिज्या की एक वृत्तीय मोड़ पर 36 किमी/घंटा से चलती है। इस पर लगा अभिकेन्द्र बल का मान होगा:
- 66एक $0.25$ किग्रा की बॉल एक $1.96$ मी लम्बे धागे में बांघकर क्षैतिज वृत्त में घुमायी जाती है। यदि धागे में तनाव $25 N$ से अधिक हो तो धागा टूट जाता है। कितने अधिकतम वेग से बॉल को घुमाओगे?View Solution
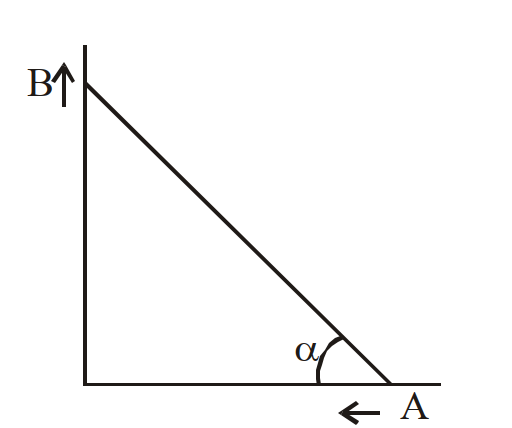
- 67दो कण $A$ तथा $B$ एक छड़ $AB$ पर है। यह छड़ लम्बवत् रेलों पर फिसलती है। $A$ का वेग बायें की ओर 10 मी/सेकंड है तो $B$ का वेग होगा यदि $\alpha=60^{\circ}$View Solution
- 68एक बिन्दु $\overrightarrow{ r }=7 \hat{ i }+3 \hat{ j }+ k$ पर बल $\overrightarrow{ F }=-3 \hat{ i }+\hat{ j }+5 \hat{ k }$ कार्यरत है। है इसका आघूर्ण है।View Solution
- 69एक बॉल को क्षैतिज से $45^{\circ}$ के कोण पर प्रक्षेपित किया जाता है। इसकी गतिज ऊर्जा $E$ है। उच्चतम बिन्दु पर गतिज ऊर्जा होगी-View Solution
- 70एक पिण्ड को क्षैतिज वृत्त ( $r=20$ सेमी) में कोणीय वेग 10 रेडियन/सेकंड से घुमाया जाता है। इसका रेखीय वेग होगा-View Solution
- 71View Solutionनिम्न में से कौन सी राशि सदिश नहीं है?
- 72एक बंदूक से एक गोली 1000 मी/सेकंड से 100 मी दूर किसी लक्ष्य पर दागी जाती है। लक्ष्य से कितनी ऊंचाई पर बंदूक को रखना होगा? (हवा का घर्षण नगण्य है तथा $g=10$ मी $/$ सेकंड $^2$ )View Solution
- 73एक कण का स्थिति सदिश $ \vec{r}=(a \cos \omega \hat{i})+(a \sin \omega t) \hat{j} $ है। इस कण का वेग:View Solution
- 74$Y$ दिशा में गतिश्तील एक पिण्ड पर बल $\overrightarrow{ F }=(-2 \hat{ i }+15 \hat{ j }+6 \hat{ k }) N$ कार्यतर है। यदि यह $Y$ दिशा में 10 मीटर चला हो तो किया गया कार्य है।View Solution
- 75View Solutionजब एक पिण्ड एक वृत्तीय पथ पर समान चाल से चलता हो तो:
- 76View Solutionएक नाव को 8 किमी/घंटा से एक नदी के पार भेजा जाता है। यदि नाव का परिणामी वेग 10 किमी/घंटा हो तो नदी के बहाव का वेग है :
- 77$\overrightarrow{ A } \times 0$ का परिणाम होगाView Solution
- 78$M$ द्रव्यमान का एक पिण्ड $A , V$ वेग से क्षैतिज से $30^{\circ}$ तथा समान द्रव्यमान दूसरा पिण्ड $B$ समान वेग से क्षैतिज से $60^{\circ}$ पर प्रक्षेपित किया जाता है। उनके क्षैतिज परासों का अनुपात होगाView Solution
- 79View Solutionदूध में से क्रीम निकालने के लिए उसे मथा जाता है तो बताओ कौन सा बल कार्य करता है?
- 80View Solutionएक गोली की अधिकतम परास 16 किलोमीटर है। गोली किस वेग से बंदूक से निकली थी।
- 81एक विद्युत पंखे के ब्लेड की घूर्णन अक्ष से लम्बाई 30 सेमी है। पंखा $120 rpm$ से चलता है। पंखे के ब्लेड के अग्र भाग का त्वरण होगाView Solution
- 82दो पिण्ड समान द्रव्यमान तथा समान वेग से $30^{\circ}$ तथा $60^{\circ}$ पर प्रक्षिप्त किये जाते है। इनके क्षैतिज परासों का अनुपात होगाView Solution
- 83यदि $\overrightarrow{ A }$ तथा $\overrightarrow{ B }$ के बीच कोण $\theta$ है तो $\overrightarrow{ A } \cdot(\overrightarrow{ B } \times \overrightarrow{ A })$ का मान हैView Solution
- 84एक बस सड़क पर उत्तर दिशा में 50 किमी/घंटा के समान वेग से चलती है। यह $90^{\circ}$ पर मुड़ती है। तथा मुड़ने के बाद भी चाल समान रहती है। मुड़ने के दौरान वेग में कितनी बढ़ोतरी हुई।View Solution
- 85तीन सदिश $\overrightarrow{ A }, \overrightarrow{ B }$ तथा $\overrightarrow{ C }$ के परिणाम क्रमशः 3,4 , 5 मात्रक है। यदि $\overrightarrow{ A }+\overrightarrow{ B }=\overrightarrow{ C }$ तो $\overrightarrow{ A }$ तथा $\overrightarrow{ B }$ के बीच का कोण है।View Solution
- 86कोई कार त्रिज्या $R$ की वक्रित सड़क पर गतिमान है। सड़क कोण $\theta$ पर झुकी है। कार के टायरों और सड़क के घर्पण-गुणांक $\mu_{ s }$ है। इस सड़क पर कार का अधिकतम सुरक्षा वेग है:View Solution
- 87$R$ त्रिज्या के किसी ऊर्ध्वाधर पाश (लूप) में $m$ द्रव्यमान के किसी पिण्ड को किस निम्नतम वेग से प्रवेश करना चाहिए कि वह पाश को पूर्ण कर सके?View Solution
- 88दो पत्थरों के द्रव्यमान $m$ तथा $2 m$ है, भारी पत्थर को $\frac{ r }{2}$ त्रिज्या के तथा हल्के पत्थर को $r$ त्रिज्या के वृताकार क्षैतिज पथों में घुमाया जाता है। जब ये पत्थर एक समान अभिकेन्द्रीय बल अनुभव करते है, तब हल्के पत्थर का रेखीय वेग भारी पत्थर के रेखीय वेग का $n$ गुना है $n$ का मान है:View Solution
- 89किसी तख्ते के एक सिरे पर एक बक्सा रखा है। तख्ते के उस सिरे को धीरे - धीरे ऊपर की ओर उठाया जाता है। तख्ते के क्षैतिज से $30^{\circ}$ कोण बनाने पर बक्सा नीचे की ओर फिसलना प्रारम्भ करता है और $4.0 s$ में $4.0 m$ दूरी तय कर लेता है? तो बक्से तथा तख्ते के बीच स्थैतिक तथा गतिक घर्पण गुणांको का क्रमश: मान होगा:View Solution
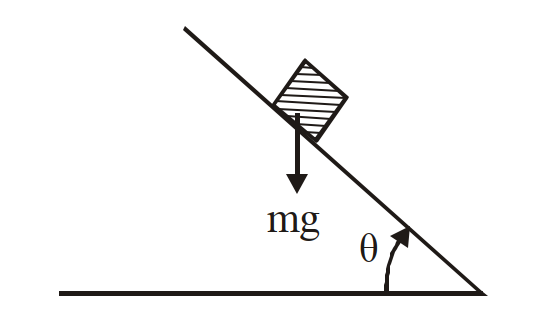
- 90$m$ द्रव्यमान का एक बैलून (गुब्बारा) $a$ त्वरण से नीचे उतर रहा है (जहाँ $a < g$ )। इसमें से कितने द्रव्यमान का पदार्थ हटा दिया जाय कि यह $a$ त्वरण से ऊपर की ओर जाने लगे ?View Solution
- 91यहां दर्शाये गये निकाय में तीन पिण्ड $m _1, m _2$ तथा $m _3$ एक रस्सी से जुड़े हैं जो एक घिरनी $P$ के ऊपर होकर गुजरती है। $m _1$ मुक्त रूप से लटका है और $m _2$ तथा $m _3$ एक रूक्ष क्षैतिज मेज पर है, जिसका घर्षण गुणांक $\mu$ है। घिरनी घर्षणरहित है और इसका द्रव्यमान नगण्य है। यदि $m _1= m _2= m _3= m$ है, तो $m _1$ का अधोमुखी ( नीचे की ओर) त्वरण होगाView Solution
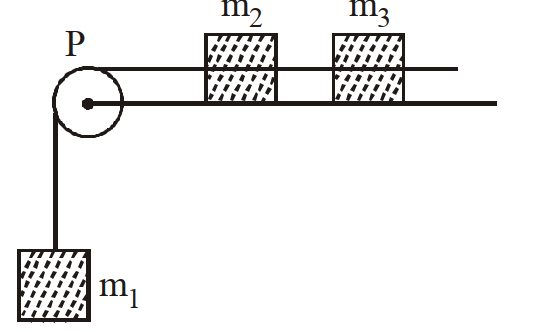
- 92$m$ द्रव्यमान के किसी कण पर आरोपित बल $F$ को बल समय ग्राफ द्वारा दर्शाया गया है। समय $t =0$ से $t =8$ सेकण्ड तक के अन्तराल में कण के संवेग में परिवर्तन होगाView Solution
- 93किसी नत-समतल का कोण $\theta$ है। उसका ऊपरी आधा भाग पूर्णतः चिकना है तथा निचला आधा भाग खुरदरा है। इस नत-समतल के ऊपरी सिरे से एक ब्लॉक (गुटका) नीचे की ओर फिसलता है। यदि गुटका प्रारंभ में विराम स्थिति में था तो, फिसलते हुए, वह नत-समतल की तली पर फिर से विराम अवस्था में आ जायेगी जब गुटके और नत समतल के नीचे आधे भाग के बीच घर्षण गुणांक का मान हो:View Solution
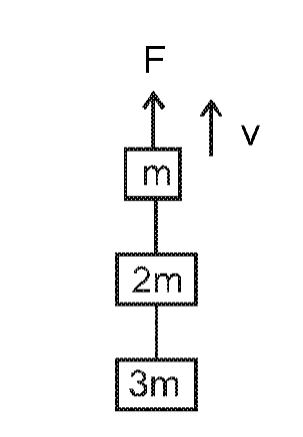
- 94तीन ब्लॉकों (गुटकों) के द्रव्यमान क्रमश : $m , 2 m$ तथा $3 m$ हैं, ये आरेख (चित्र) में दर्शाये गये अनुसार डोरियों से जुड़े हैं। $m$ ब्लॉक पर ऊपर की ओर $F$ बल लगाने पर, सभी गुटके एक स्थिर वेग $v$ से, ऊपर की ओर गति करते हैं। $2 m$ द्रव्यमान के ब्लॉक पर नेट बल कितना है? ( $g$ गुरुत्वीय त्वरण है)View Solution
- 95$m$ द्रव्यमान की एक कार, $R$ त्रिज्या के किसी वृत्ताकार समतल पथ पर गति कर रही है। यदि सड़क तथा कार के टायरों के बीच स्थैतिक घर्षण $\mu_s$ हो तो, वृत्तीय गति में कार की अधिकतम चाल होगी :View Solution
- 96एक पत्थर को $h$ ऊँचाई से गिराया जाता है। यह एक निश्चित संवेग $P$ से भू-तल से टकराता है, यदि इसी पत्थर को, इस ऊँचाई से $100 \%$ अधिक ऊँचाई से गिराया जाये तो भू-तल से टकराते समय इसके संवेग में परिवर्तन होगा :View Solution
- 97$1000 kg$ द्रव्यमान की एक कार घर्षणहीन सड़क पर 90 $m$ त्रिज्या के एक ढालू (झुके हुए) मोड़ से गुजरती है। यदि मोड़ का झुकाव कोण $45^{\circ}$ हो तो, कार की चाल है :View Solution
- 98एक संवाहक पट्टा $2 m / s$ की स्थिर चाल से घूर्णन कर (घूम) रहा है। एक बक्से को इसके ऊपर धीरे से रखा जाता है। इन दोनों के बीच घर्षण गुणांक $\mu=0.5$ है। तो पट्टे पर विराम अवस्था में आने से पहले पट्टे के सापेक्ष बक्से के द्वारा तय की गई दूरी $g$ का मान $10 ms ^{-2}$, लेते हुए होगी:View Solution
- 99एक वस्तु का द्रव्यमान $M$ है, यह एक दृढ़ दीवार पर $v$ वेग से अभिलम्बवत् टकराती है और इसी वेग से वापस लौट जाती है। वस्तु पर लगा आवेग होगा:View Solution
- 100एक व्यक्ति का द्रव्यमान $60 kg$ है। वह $940 kg$ द्रव्यमान के लिफ्ट में खड़ा होकर लिफ्ट का बटन दबाता है, जिससे लिफ्ट $1.0 m / s ^2$ के त्वरण से ऊपर की ओर गति करती हैं। यदि $g =10 ms ^{-2}$ हो तो, उस केबल में, जिससे लिफ्ट लटकी रहती है, तनाव होगा:View Solution