Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1क्या अनुक्रम $0, 2, 0, 2, ...$ एक $AP$ बनाता है? अपने जवाब का औचित्य साबित करें।View Solution
- 2क्या अनुक्रम $-1, -1, -1, -1, ...$ एक $AP$ बनाता है? आपने जवाब का औचित्य साबित करें।View Solution
- 3यदि किसी $AP$ का सार्व अंतर $5$ है, तो $a_{18 }- a_{13}$ क्या है?View Solution
- 4$AP: 21, 42, 63, 84, ...$ का कौन$-$सा पद $210$ है?View Solution
- 5यदि किसी $AP$ का दूसरा पद $13$ और $5$वाँ पद $25$ है, तो उसका $7$वाँ पद क्या है?View Solution
- 6उस $AP,$ जिसके प्रथम दो पद $-3$ और $4$ हैं, का $21$वाँ पद हैView Solution
- 7उस $AP,$ जिसका प्रथम पद$-2$ और सार्व अंतर$-2$ है, के प्रथम चार पद हैंView Solution
- 8$AP: -5, \frac{-5}{2}, 0, \frac{5}{2}, ... $ का $11$वाँ पद हैView Solution
- 9View Solutionसंख्याओं -10, -6, -2, 2, ... की सूची
- 10किसी $AP$ में, यदि $a = 3.5, d = 0$ और $n_{ }= 101$ है, तो $a$ बराबर है:View Solution
- 11$3$ के प्रथम पाँच गुणजों का योग हैView Solution
- 12किसी $AP$ में, यदि $a = 1, a_{n }= 20$ और $S_{n }= 399$ हों, तो $n$ बराबर हैView Solution
- 13$AP: 10, 6, 2, ...$ के प्रथम $16$ पदों का योग हैView Solution
- 14यदि किसी $AP$ का प्रथम पद $-5$ और सार्व अंतर $2$ है, तो उसके प्रथम $6$ पदों का योग हैView Solution
- 15View Solutionप्रथम 100 प्राकृत संख्याओं के योग को ज्ञात करने से संबद्ध प्रसिद्ध गणितज्ञ है
- 16$AP: -11, -8, -5, ..., 49$ के अंत से चौथा पद हैView Solution
- 17यदि किसी $AP$ के $7$वें पद का $7$ गुना उसके $11$वें पद के $11$ गुने के बराबर हो, तो उसका $18$ वाँ पद होगाView Solution
- 18दो समांतर श्रेढ़ियों का एक ही सार्व अंतर है। इनमें से एक का प्रथम पद $-1$ और दूसरी का प्रथम पद $-8$ है। तब, इनके चौथे पदों के बीच का अंतर हैView Solution
- 19उस $AP$ का सार्व अंतर क्या है, जिसमें $a_{18 }- a_{14 }= 32$ क्या है?View Solution
- 20किसी $AP$ में, यदि $d = -4, n = 7$ और $a_{n }= 4$ है, तो $a$ का मान है।View Solution
- 21किसी $AP$ का $n$ वाँ पद $n^{2 }+ 1$ नहीं हो सकता। अपने उत्तर का औचित्य दीजिए।View Solution
- 22दिव्या ने $1000 ₹\ 10\%$ वार्षिक की दर से चक्रवृद्धि ब्याज पर जमा कराए। प्रथम वर्ष, दूसरे वर्ष, तीसरे वर्ष, $...,$ के अंत में मिश्रधन एक $AP$ बनाते हैं। अपने उत्तर का औचित्य दीजिए।View Solution
- 23$AP: 10, 5, 0, -5, ...$ का सार्व अंतर $d, 5$ के बराबर है।View Solution
- 24यदि किसी $AP$ का $9$वाँ पद शून्य है, तो सिद्ध कीजिए कि उसका $29$वाँ पद उसके $19$वें पद का दुगुना होगा।View Solution
- 25उस $AP$ का $20$वाँ पद ज्ञात कीजिए जिसका $7$वाँ पद $11$वें पद से $24$ कम है और प्रथम पद $12$ है।View Solution
- 26किसी $AP$ के $5$वें और $7$वें पदों का योग $52$ है तथा $10$ वाँ पद $46$ है। वह $AP$ ज्ञात कीजिए।View Solution
- 27किसी $AP$ के $26$वें, $11$वें और अंतिम पद क्रमशः $0, 3$ और $-\frac 15$ हैं। इसका सार्व अंतर और पदों की संख्या ज्ञात कीजिए।View Solution
- 28वह $AP$ निर्धारित कीजिए जिसका पाँचवाँ पद $19$ है तथा आठवें पद का तेरहवें पद से अंतर $20$ है।View Solution
- 29View Solutiona, b और c के ऐसे मान ज्ञात कीजिए कि संख्याएँ a, 7, b, 23, c एक AP में हों।
- 30यासमीन पहले महीने में $32 ₹$ की बचत करती है, दूसरे महीने में $36 ₹$ की बचत करती है तथा तीसरे महीने में $40 ₹$ की बचत करती है। यदि वह इसी प्रकार बचत करती रहे, तो कितने महीने में वह $2000 ₹$ की बचत कर लेगी?View Solution
- 31कनिका को उसका जेब खर्च $1$ जनवरी $2008$ को दिया गया। वह इसमें से अपने पिग्गी बैंक में पहले दिन $1 ₹$ डालती है, दूसरे दिन $2 ₹$ डालती है, तीसरे दिन $3 ₹$ डालती है तथा ऐसा ही महीने के अंत तक करती रहती है। उसने अपने जेब खर्च में से $204 ₹$ खर्च भी किए और पाया कि महीने के अंत में उसके पास अभी भी $100 ₹$ शेष हैं। उस महीने उसको कितना जेब खर्च मिला था?View Solution
- 32प्रथम पद $8$ और सार्व अंतर $20$ वाली एक $AP$ के प्रथम $n$ पदों का योग एक अन्य $AP$ के प्रथम $2n$ पदों के योग के बराबर है, जिसका प्रथम पद $-30$ और सार्व अंतर $8$ है। $n$ ज्ञात कीजिए।View Solution
- 33AP के पहले तीन पद लिखिए, जहाँ a = $\sqrt 2$ और d = $\frac 1{\sqrt 2}$ हैं:View Solution
- 34$AP: -15, -13, -11, ...$ का योग $-55$ बनाने के लिए इसके कितने पदों की आवश्यकता होगी? दो उत्तर प्राप्त होने का कारण स्पष्ट कीजिए।View Solution
- 35View SolutionAP के पहले तीन पद लिखिए, जहाँ a = -5 और d = -3 हैं:
- 36ऐसी प्रथम सात संख्याओं का योग ज्ञात कीजिए, जो $2$ का गुणज हैं और $9$ का भी गुणज हैं।View Solution
- 37AP के पहले तीन पद लिखिए, जहाँ a = $\frac 12$और d = -$\frac 16$ हैं:View Solution
- 38$AP: 8, 10, 12, ..., 126$ के अंतिम $10$ पदों का योग ज्ञात कीजिए।View Solution
- 39उस $AP$ के सभी $11$ पदों का योग ज्ञात कीजिए, जिसका मध्य पद $30$ है।View Solution
- 40यदि किसी $AP$ के प्रथम $6$ पदों का योग $36$ है तथा प्रथम $16$ पदों का योग $256$ है, तो उसके प्रथम $10$ पदों का योग ज्ञात कीजिए।View Solution
- 41उस $AP$ के प्रथम $17$ पदों का योग ज्ञात कीजिए, जिसके चौथे और $9$वें पद क्रमशः $-15$ और $-30$ हैं।View Solution
- 42यदि $S_n$ किसी $AP$ के प्रथम $n$ पदों का योग व्यक्त करता है, तो सिद्ध कीजिए कि $S_{12 }= 3(S_{8 }- S_4)$ है।View Solution
- 43किसी $AP$ में यदि $S_{n }= 3n^{2 }+ 5n$ और $a_{k }= 164$ है, तो $k$ का मान ज्ञात कीजिए।View Solution
- 44सत्यापित करें कि $2, 2a + 1, 3a + 2, 4a + 3, ... AP$ है, और फिर इसके अगले तीन पद लिखिए।View Solution
- 45किसी $AP$ में, यदि $S_{n }= n(4n + 1)$ है, तो $AP$ ज्ञात कीजिए।View Solution
- 46सत्यापित करें $a + b, (a + 1) + b, (a + 1) + (b + 1), ... AP,$ और फिर इसके अगले तीन पद लिखिए।View Solution
- 47यदि $a_{n }= 3 - 4n$ हो, तो दर्शाइए कि $a_1, a_2, a_3, ...$ एक $AP$ बनाते हैं। $S_{20}$ भी ज्ञात कीजिए।View Solution
- 48सत्यापित करें की $\sqrt 3, 2\sqrt 3, 3\sqrt 3, ...$ एक $AP$ है, और फिर इसके अगले तीन पद लिखिए।View Solution
- 49$AP: -2, -7, -12, ...$ का कौन$-$सा पद $-77$ है? पद $-77$ तक इस $AP$ का योग ज्ञात कीजिए।View Solution
- 50सत्यापित करें की $5, \frac{14}{3}, \frac{13}{3}, 4, ...$ एक $AP$ है, और फिर इसके अगले तीन पद लिखिए।View Solution
- 51योग ज्ञात कीजिए: $\frac{a-b}{a+b}+\frac{3 a-2 b}{a+b}+\frac{5 a-3 b}{a+b} + ...11$ पदों तकView Solution
- 52योग ज्ञात कीजिए: $4-\frac 1n + 4-\frac 2n + 4-\frac 3n + ...n$ पदों तकView Solution
- 53योग ज्ञात कीजिए: $1 + (–2) + (–5) + (–8) + ... + (–236)$View Solution
- 54सत्यापित करें की $0, \frac{1}{4}, \frac{1}{2}, \frac{3}{4}, ...$ एक $AP$ है, और फिर इसके अगले तीन पद लिखिए।View Solution
- 55किसी $AP$ का प्रथम पद $-5$ और अंतिम पद $45$ है। यदि इस $AP$ के पदों का योग $120$ हो, तो पदों की संख्या और सार्व अंतर ज्ञात कीजिए।View Solution
- 56$A.P: -\frac 43, -1, -\frac 23, ..., 4\frac 13$ के दोनों मध्य पदों का योग ज्ञात कीजिए।View Solution
- 57$10$ और $300$ के बीच में स्थित ऐसी कितनी संख्याएँ हैं, जिनको $4$ से भाग देने पर शेषफल $3$ रहता है?View Solution
- 58$AP: 53, 48, 43, ...$ में प्रथम ऋणात्मक पद कौन$-$सा होगा?View Solution
- 59View SolutionAP: -2, -4, -6, ..., -100 का अंत से 12वाँ पद ज्ञात कीजिए।
- 60यदि किसी $AP$ के तीसरे और $8$वें पदों का योग $7$ है तथा $7$वें और $14$वें पदों का योग $-3$ है, तो उसका $10$वाँ पद ज्ञात कीजिए।View Solution
- 61यदि दो समांतर श्रेढ़ियों $9, 7, 5 ...$ और $24, 21, 18, ...$ के $n$वें पद एक ही हैं, तो $n$ का मान ज्ञात कीजिए। साथ ही, वह पद भी ज्ञात कीजिए।View Solution
- 62View Solutionकिसी त्रिभुज के कोण एक AP में हैं। सबसे बड़ा कोण सबसे छोटे कोण का दुगुना है। त्रिभुज के सभी कोण ज्ञात कीजिए।
- 63View Solution207 को तीन ऐसे भागों में विभक्त कीजिए कि ये भाग एक AP में हों तथा दो छोटे भागों का गुणनफल 4623 हो।
- 64$k$ का मान ज्ञात कीजिए ताकि $k^{2 }+ 4k + 8, 2k^{2 }+ 3k + 6, 3k^{2 }+ 4k + 4$ किसी $AP$ के तीन क्रमागत पद हों।View Solution
- 65ज्ञात कीजिए कि $55$ एक $AP: 7, 10, 13, ...$ का पद है या नहीं। यदि हाँ, तो ज्ञात कीजिए कि यह कौन$-$सा पद है।View Solution
- 66स्तंभ $A$ में दी हुई प्रत्येक $AP$ को स्तंभ $B$ में दिए उपयुक्त सार्व अंतर से सुमेलित कीजिए:View Solution
स्तंभ $A$ स्तंभ $B$ $(a) 2, -2, -6, -10, ...$ $(i) \frac 23$ $(b) a = -18, n = 10, a_n = 0$ $(ii) -5$ $(c) a = 0, a_{10} = 6$ $(iii) 4$ $(d) a_2 = 13, a_4 = 3$ $(iv) -4$ $(v) 2$ $(vi) \frac 12$ $(vii) 5$ - 67किसी $AP$ के प्रथम तीन पदों का योग $33$ है। यदि पहले और तीसरे पदों का गुणनफल दूसरे पद से $29$ अधिक है, तो वह $AP$ ज्ञात कीजिए।View Solution
- 68$AP: -11, -7, -3, ..., 49$ के बीचो$-$बीच $($मध्य$)$ वाला $($वाले$)$ पद $($पदों$)$ का $($के$)$ मान ज्ञात कीजिए।View Solution
- 69View Solutionयदि संख्याएँ n - 2, 4n - 1 और 5n + 2 किसी AP में हैं, तो n का मान ज्ञात कीजिए।
- 70जसपाल सिंह अपने कुल $₹ 118000$ के ऋण को मासिक किस्तों में, $₹ 1000$ की पहली किस्त से प्रारंभ करते हुए, चुकाता है। यदि वह प्रति मास की किश्त $₹ 100$ बढ़ाता जाता है, तो उसके द्वारा $30$ वीं किस्त में कितनी राशि चुकाई जाएगी? $30$ वीं किस्त के बाद उसको कितना ऋण चुकाना और शेष रहेगा?View Solution
- 71समीकरण $-4 + (-1) + 2 + ... + x = 437$ को हल कीजिए।View Solution
- 72दर्शाइए कि उस $AP$ का योग, जिसका प्रथम पद $a,$ द्वितीय पद $b$ और अंतिम पद $c$ हो, $\frac{(a+c)(b+c-2 a)}{2(b-a)}$ के बराबर है।View Solution
- 73View Solutionकिसी AP के 11 वें पद का 18 वे पद से अनुपात 2:3 है। 5 वें पद का 21 वें पद से अनुपात ज्ञात कीजिए तथा साथ ही प्रथम पाँच पदों के योग का प्रथम 21 पदों के योग से अनुपात ज्ञात कीजिए।
- 74$100$ और $200$ के बीच उन पूर्णांकों का योग ज्ञात कीजिए जो $9$ से विभाज्य नहीं हैं।View Solution
- 75$100$ और $200$ के बीच के उन पूर्णांकों का योग ज्ञात कीजिए जो $9$ से विभाज्य हैं?View Solution
- 76किसी $AP$ में $37$ पद हैं। बीचो$-$बीच के तीन पदों का योग $225$ है तथा अंतिम तीन पदों का योग $429$ है। वह $AP$ ज्ञात कीजिए।View Solution
- 77किसी $AP$ का $8$वाँ पद उसके दूसरे पद का आधा है तथा $11$वाँ पद उसके चौथे पद के एक तिहाई से $1$ अधिक है। $15$वाँ पद ज्ञात कीजिए।View Solution
- 78$1$ से $500$ तक के सभी पूर्णांकों का योग ज्ञात कीजिए जो $2$ या $5$ के गुणज हैं। $[$संकेत: ये संख्याएँ होंगी: $2$ के गुणज $+ 5$ के गुणज $- 2$ के गुणज और साथ ही $5$ का भी$]$View Solution
- 79$1$ से $500$ तक के उन पूर्णांकों का योग ज्ञात कीजिए जो $2$ और $5$ के भी गुणज हैं।View Solution
- 80$1$ और $500$ के बीच सभी पूर्णांकों का योग ज्ञात कीजिए जो $2$ और $5$ के भी गुणज हों।View Solution
- 81किसी स्कूल के विद्यार्थियों ने, स्कूल के वार्षिक दिवस के उपलक्ष्य में, स्कूल के सीधे मार्ग पर रंगीन झंडियाँ लगाकर स्कूल को सजाने का निर्णय लिया। उनके पास $27$ झंडियाँ थीं जिन्हें प्रत्येक $2$ मीटर के अंतराल पर लगाया जाना है। इन झंडियों को बीचो$-$बीच की झंडी के स्थान पर एकत्रित कर लिया जाता है। झंडियाँ लगाने का कार्य रुचि को सौंपा गया। रुचि ने अपनी पुस्तकें वहीं रख दीं जहाँ झंडियों को एकत्रित किया गया था। वह एक बार में केवल एक ही झंडी ले जा सकती है। उसने इस कार्य को पूरा करने तथा अपनी पुस्तकें ले आने के लिए कुल कितनी दूरी तय की? एक झंडी हाथ में लिए हुए आते अधिकतम कितनी दूरी तय की?View Solution
- 82किसी $AP$ के प्रथम पाँच पदों के योग और उसी $AP$ के प्रथम सात पदों के योग का योग $167$ है। यदि इस $AP$ के प्रथम दस पदों का योग $235$ है, तो इसके प्रथम $20$ पदों का योग ज्ञात कीजिए।View Solution
- 83समीकरण $1 + 4 + 7 + 10 + ... + x = 287$ को हल कीजिए।View Solution
- 84किसी $AP$ में चार क्रमागत संख्याओं का योग $32$ है तथा पहले और अंतिम संख्याओं के गुणफल और दो मध्य संख्याओं के गुणफल का अनुपात $7:15$ है। वे संख्याएँ ज्ञात कीजिए।View Solution
- 85$\triangle ABC \sim \triangle DFE, \angle \mathrm{A} = 30^\circ, \angle \mathrm{C} = 50^\circ, AB = 5 \ cm, AC = 8 \ cm$ और $DF = 7.5 \ cm$ दिया हुआ है। तब, निम्नलिखित सत्य है:View Solution
- 86यह दिया है कि $\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{1}{3}$ के साथ $\triangle $ABC $\sim$ $\triangle $PQR है। तब $\frac{\operatorname{ar}(\mathrm{PRQ})}{\operatorname{ar}(\mathrm{BCA})}$ बराबर हैView Solution
- 87त्रिभुजों ABC और DEF में, $\angle {B}=\angle {E}$, $\angle {F}=\angle {C}$ तथा AB = 3 DE है। तब दोनों त्रिभुज हैंView Solution
- 88यदि दो त्रिभुजों DEF और PQR मे, $\angle {D}=\angle {Q}$ और $\angle {R}=\angle {E}$ है, तो निम्नलिखित में से कौन सत्य नहीं है?View Solution
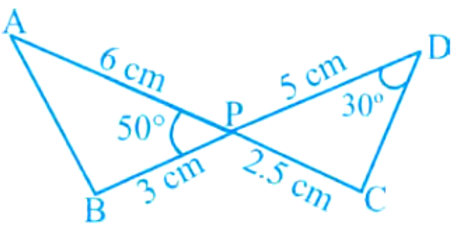
- 89आकृति में, दो रेखाखंड $AC$ और $BD$ परस्पर बिंदु $P$ पर इस प्रकार प्रतिच्छेद करते हैं कि $PA = 6 \ cm, PB = 3 \ cm, PC = 2.5 \ cm, PD = 5 \ cm, \angle APB = 50^\circ$ और $\angle CDP = 30^\circ$ है तब$, \angle PBA$ बराबर हैView Solution
- 90यदि दो त्रिभुजों ABC और PQR मे, $\frac{{AB}}{{QR}}=\frac{{BC}}{{PR}}=\frac{{CA}}{{PQ}}$ है, तोView Solution
- 91यदि $\triangle$ABC $\sim$ $\triangle$EDF और $\triangle$ABC, $\triangle$DEF के समरूप नहीं है, तो निम्नलिखित में से कौन सत्य नहीं है?View Solution
- 92एक समचतुर्भुज के विकर्णों की लंबाइयाँ $16 \ cm$ और $12 \ cm$ हैं। तब इस समचतुर्भज की भुजा की लंबाई हैView Solution
- 93यदि $\triangle \text{PQR}$ की एक भुजा $PQ$ पर $S$ एक ऐसा बिंदु है कि $PS = QS = RS$ है, तोView Solution
- 94यदि $\triangle$ABC $\sim$ $\triangle$QRP, $\frac{\operatorname{ar}(\mathrm{A} \mathrm{BC})}{\operatorname{ar}(\mathrm{PQR})}=\frac{9}{4}$, AB = 18 cm और BC = 15 cm है, तो PR बराबर हैView Solution
- 95यदि त्रिभुज ABC और DEF में, $\frac{{A} {B}}{{DE}}=\frac{{BC}}{{FD}}$ है, तो ये समरूप होंगे, जबView Solution
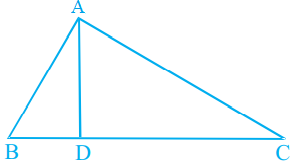
- 96आकृति में, $\angle BAC = 90^o$ और $AD \perp BC$ हैं। तब,View Solution
- 97View Solutionएक त्रिभुज ABC की भुजाओं AB और AC पर क्रमशः बिंदु D और E इस प्रकार स्थित हैं कि AD = 2 cm, BD = 3 cm, BC = 7.5 cm और DE||BC है। तब, DE की लंबाई (cm में) है
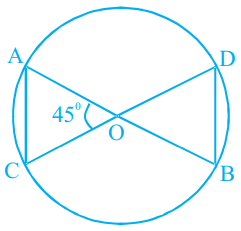
- 98यदि आकृति में, $O$ दो जीवाओं $AB$ और $CD$ का प्रतिच्छेद बिंदु इस प्रकार है कि $\text{OB = OD}$ है, तो त्रिभुज $\text{OAC}$ और $\text{ODB}$ हैंView Solution
- 99दो समरूप त्रिभुजों के संगत शीर्षलंबों का अनुपात $\frac{3}{5}$ है। क्या यह कहना सही है कि इन त्रिभुजों के क्षेत्रफलों का अनुपात $\frac{6}{5}$ है? क्यों?View Solution
- 100View Solutionयदि दो समकोण त्रिभुजों में, एक त्रिभुज का एक न्यून कोण दूसरे त्रिभुज के एक न्यून कोण के बराबर हो, तो क्या आप कह सकते हैं कि दोनों त्रिभुज समरूप होंगे? क्यों?